Trigonometrian historia sen alkuperästä

Se Trigonometriahistoria Se viittaa tosiasioihin ja edistyksiin, joita tapahtui tämän matematiikan haaran ympärillä sen alkuperästä viimeisimpiin tapahtumiin.

Kun teet lyhyen matkan historiansa läpi, on selvää, että tämä tiede syntyi vastauksena muinaisten tähtitieteilijöiden ja navigaattoreiden ongelmiin analysoida taivaan tähtien siirtymistä taivaassa.

Termi ilmestyy ensimmäistä kertaa kirjassa Trigonometriae Libri Quinque, jonka on kirjoittanut saksalainen matemaatikko ja tutkija Pitiscus Bartolomé (1561-1613). Via Wikimedia Commons.

Samoin sana trigonometria syntyy kahden kreikkalaisen sanan koostumuksesta: Trigononi (kolmio) ja Metroni (laajuus). Termi ilmestyy ensimmäistä kertaa kirjassa Trigonometriae libri quinque, Kirjoittanut Saksan matemaatikko ja tutkija Pitiscus Bartolomé (1561-1613).

Tällä tavoin sanan etymologia osoittaa, että trigonometria on tutkimus kolmion kulmien ja sen muodostavien segmenttien tai viivojen välillä.

[TOC]

Trigonometrian alku

Ihminen suoritti trigonometrian ensimmäiset vaiheet, kun sitä edistettiin tarve tuntea ja analysoida tähtien liikettä.

Toisin sanoen ihmisen suunnittelema trigonometria, koska se löydettiin tilanteista, joissa oli mahdotonta tehdä mittauksia suoraan, koska tähtien laskemiseksi vaadittiin monimutkaisempia matemaattisia työkaluja.

- Babylon -tutkimukset

Mutapöytä, jonka on kirjoittanut babylonialaiset nimeltään Plimpton 322. Via: Wikimedia Commons

Tutkimukset osoittavat, että yli 3 sitten.000 vuotta babylonialaiset käsittivät jo kulman ja trigonometristen syiden käsitteen, ts. He pystyivät luomaan suhteet osapuolten ja kolmioiden kulmien välillä.

Esimerkiksi babylonialaisten kirjoittama mutapöytä - nimeltään Plimpton 322 (1800 a. C.) näyttää peräkkäisen sarakkeita ja rivejä, jotka sisältävät numeroita cuneiform -kirjoituksessa. Joidenkin asiantuntijoiden suorittaman tutkimuksen mukaan tämä tabletti edustaa sitä, mikä näyttää olevan sarja trigonometrisiä funktioita.

Voi palvella sinua: mikä on ohje? (Geometria)

Babylonialaiset tunsivat käsitteet, jotka aiheuttivat Pythagorasin lauseen (569-474 a.C) ja he ymmärsivät periaatteensa.

Samoin he tiesivät myös Miletus-thales-laitteen (695-546.C), joka osoittaa, että jokainen suora, joka on piirretty yhdensuuntaisen kolmion sivun kanssa, muodostuu kahden muun puolen kanssa toinen kolmio, joka on samanlainen kuin alkuperäinen kolmio.

- Muinaiset egyptiläiset

Muinaiset egyptiläiset onnistuivat ylläpitämään kaltevuutta tasaisesti jokaisessa pyramidipinnassa. Via: Pixabay

Vaikka ei ole aiheellista puhua trigonometriasta Egyptin matematiikan yleisellä alueella, ei ole epäilystäkään siitä, että tämä sivilisaatio käsitteli tiettyjä trigonometrisiä käsitteitä.

Tämä tapahtuu, koska harkittaessa egyptiläisten, kuten pyramidien, kuten pyramidien, suuria rakennuksia voidaan päätellä, että heillä oli jonkin verran tietoa trigonometriasta.

Perustekniikan vaikeus, joihin egyptiläiset kohtaavat - ja se ratkaisi hämmästyttävän.

Tätä varten he käyttivät käsitettä, jota he kutsuivat "seqtiksi", ja se vastaa sitä, mitä ymmärrämme tänään kaltevan tasaisen pinnan kaltevuutena.

Lisäksi egyptiläiset tekevät mittauksia pystysuuntaisilla pinnoilla, joita käytetään yksikönä "kyynärpään" ja vaakasuorassa "kädessä", joka vastasi kyynärpäästä 1/7. Tällä tavalla he laskivat seqt tai vireillä eri rakennuksissa. Esimerkiksi Jufú (Queope) -pyramidissa seqt on 5 1/2 kättä kyynärpää kohti.

- Muinainen Kreikka ja merkkijono

Kaikki babylonialaisten ja muinaisten egyptiläisten tieto siirtyivät Kreikkaan, missä Matemaatikko ja Tähtitieteilijä on NIVAN (190-120 (190-120. C), jota pidetään trigonometrian isänä. Hiparco loi ”merkkijonot” -taulukot, joiden kanssa hän onnistui ratkaisemaan litteiden kolmioiden ongelmat.

NIVA HIPARCO - Lähde: Siirretty.Maksimin Wikipedia Commonsille - julkisen alueen alla

Niiden valmistamiseksi se käytti kehä tietyllä säteellä (säde on ympyrän keskikohdan ja kehän minkä tahansa kehän välinen etäisyys).

Voi palvella sinua: Ehdollinen todennäköisyys: Kaava ja yhtälöt, ominaisuudet, esimerkit

Sitten se syrjäytti säteen eri kulmien määrittelemiseksi; Kun tämä osoitti taulukossa, kulman sivuilla ja ympärysmittalla rajattujen viivan pituudella.

Nämä "jouset" osoittautuivat nykyään käyttämämme trigonometristen toimintojen taulukoiden edeltäjiksi.

- Intian maksut

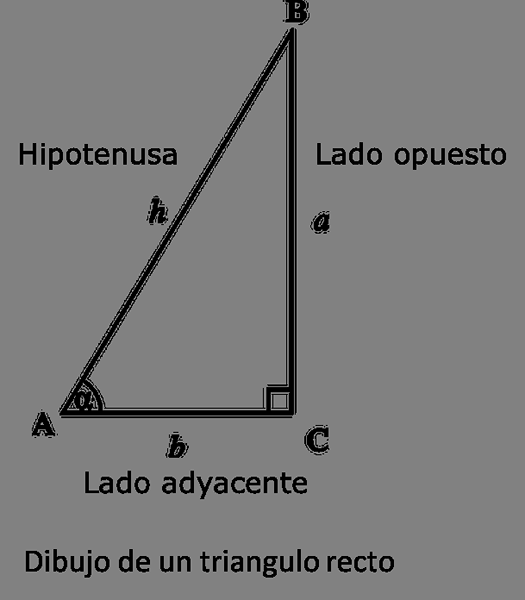Oikean kolmion piirtäminen.

Kuten Kreikan tutkijat, Intian tähtitieteilijät kehittivät myös trigonometrisen järjestelmän, mutta toisin kuin kreikkalaiset, nämä tähtitieteilijät perustivat analyysinsä "sini" -toiminnolle merkkijonojen käytön sijasta.

Näiden tähtitieteilijöiden ilmaisema "sini" -toiminto ei kuitenkaan ole nykyään käytetty; Tämä funktio ei ollut osuus (kuten nykyään käytetään), mutta vastakkaisen puolen pituus suorakulmion kolmion kulmaan, jonka hypotenuse tunnetaan.

- Arabia ja trigonometriset toiminnot

Kahdeksannen vuosisadan lopulla arabien tähtitieteilijät, joihin vaikuttavat Kreikan ja Intian kansojen suorittamat trigonometriatutkimukset, aloittivat tärkeät tutkimukset kulmien ja niiden puolien välisistä suhteista.

Tällä tavalla he nostivat 10. vuosisadan lopulla rintojen, kosinin, tangentin, kotangentin, kuivauksen ja harvesterin tunnetut toiminnot.

He löysivät ja todensivat myös primaariset trigonometrialausekkeet, joita käytetään litteiden ja pallomaisten kolmioiden analysoinnissa. Lisäksi arabimatemaatikot ehdottivat yhden arvon ("1") käyttöä radiossa (r = 1), joka aiheutti trigonometristen funktioiden nykyaikaisia ​​arvoja.

- Lännen panokset

Johann Müller, joka tunnetaan nimellä Regiomontanus (1436-1476). Geometrian alueella käytettyjen trigonometristen menetelmien systemaation ja yleistäminen ja yleistäminen. Via: Wikimedia Commons

Muinaisen Kreikan, Intian ja arabien postulaatit vaikuttivat voimakkaasti lännen matematiikkaan, erityisesti kahdestoista ja viidennentoista vuosisadan välillä.

Voi palvella sinua: chi-neliö (χ²): jakautuminen, miten se lasketaan, esimerkkejä

Tänä aikana he olivat ratkaisevia trigonometrian alueella-Johann Müllerin, joka tunnetaan myös nimellä Regiomontanus (1436-1476), panokset-. Tämä matemaatikko saavutti geometria -alueella käytettyjen trigonometristen menetelmien systemaation ja yleistämisen.

Regiomontanus kehitti ja julkaisi soittaman sopimuksen Of triangulis omnimodis libri quinque, joka koostui viidestä kirjasta ja yhteensä 131 sivua.

Tässä kirjassa hän sääteli kaikkia tasaisen ja pallomaisen trigonometrian käsitteitä, joita myöhemmin tärkeät tähtitieteilijät käyttivät: Nicolás Copernic.

- Trigonometria Seitsemännentoista ja kahdeksannentoista vuosisataa

Seitsemännentoista vuosisadan aikana trigonometrisiä laskelmia koskevat tutkimukset menestyivät matemaatikkojen, kuten skotlantilaisten John Napier (1550-1617), panoksen ansiosta, jotka nostivat erilaisia ​​menetelmiä pallomaisten kolmioiden ratkaisemiseksi.

John Napier. Lähde: By Sancard: Samuel Freeman (1773-1857) [julkinen alue], Wikimedia Commonin kautta

Myöhemmin, 1700-luvulla, sveitsiläisen matemaatikon Leonhard Eulerin (1707-1783) panokset olivat ratkaisevia, koska hänen tutkimuksensa perustivat nykyaikaisen trigonometrian perustan ottamalla käyttöön merkintä, jota tällä hetkellä käytetään trigonometrisiin toimintoihin.

Lisäksi Euler onnistui määrittelemään eksponentiaalinen funktio ja löysi suhteensa trigonometrisiin toimintoihin, mikä antoi hänelle mahdollisuuden kuvata trigonometrian ominaisuuksia.

Myöhemmin Sir Isaac Newton (1643-1727) keksimällä differentiaali- ja kiinteä laskenta helpotti suuren määrän matemaattisia toimintoja, joista on trigonometristä. Tällä tavoin trigonometriasta tuli osa matemaattista analyysiä, jossa nykyään on perustava rooli.

Esimerkki Sir Isaac Newtonista

Viitteet

1. Mansfield, Daniel. Wildberger, n. (2017). Plimpton 322 on Babylonian tarkka seksuaalinen trigonometria. Haettu 20. toukokuuta 2020: ScienEdirect.com
2. Jimenez S. (2017). Trigonometrian ja sen sovellusten historia. Haettu 23. toukokuuta 2020 Deedu
3. Pérez, V. (2010). Trigonometriahistoria. Haettu 22. toukokuuta 2020: Laguia2000.com
4. S.-Lla. (S.F.-A Trigonometria. Haettu 23. toukokuuta 2020: Blogspot.com
5. Merlet, Jean-Pierre (2004). Huomautus trigonometristen funktioiden historiasta. Haettu 22. toukokuuta 2020: Verkko
6. Adamek, t., Penkalki, k., Ystävänpäivä, G. (2005). Trigonometrian historia. Haettu 23. toukokuuta 2020: Citseseerx.Istti.PSU.Edu/