Homotecia

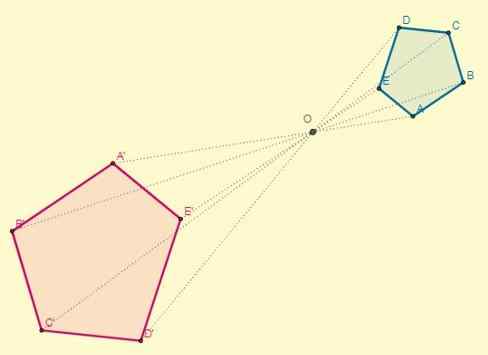
Se Homotecia Se on geometrinen muutos tasossa, jossa kiinteästä pisteestä, jota kutsutaan keskustaksi (O), etäisyydet kerrotaan yhteisellä tekijällä. Tällä tavalla jokainen piste p vastaa muunnoksen toista pistettä, ja ne ovat linjassa pisteen kanssa tai.

Sitten homotecia on vastaavuus kahden geometrisen hahmon välillä, jossa transformoituja pisteitä kutsutaan homotetisiksi, ja ne kohdistuvat kiinteään pisteeseen ja rinnakkais segmenttien kanssa keskenään.

Selitys ja kaava

Homotecia on muuntaminen, jolla ei ole yhtenäistä kuvaa, koska kuvasta he saavat yhden tai useamman suuremman tai pienemmän koon luvut kuin alkuperäinen kuva; toisin sanoen homotecia muuttaa monikulmion toiseksi vastaavaksi.

Jotta homotecia toteutuu, pisteeseen pisteeseen ja suoran linjan on vastattava, niin että homologisten pisteiden parit ovat linjassa kolmannen kiinteän pisteen kanssa, joka on Homotecian keskus.

Samoin yhdistävien linjojen parien tulisi olla yhdensuuntaisia. Tällaisten segmenttien välinen suhde on vakio, nimeltään homotecia (k) syy; siten, että homotecia voidaan määritellä seuraavasti:

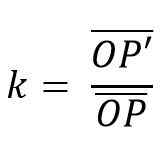
Tämän tyyppisen muutoksen tekemiseksi alkaa mielivaltainen kohta, joka on Homotecian keskipiste.

Tästä hetkestä lähtien linjasegmenttejä piirretään transformatavan kuvan jokaiselle kärkipisteelle. Asteikko, jolla uuden luvun lisääntyminen annetaan Homotecia (k): n syystä.

Homotecia -ominaisuudet

Yksi Homotecian pääominaisuuksista on, että kaikki homotecia (k) syyt kaikki homotetiset luvut ovat samanlaisia. Seuraavat ovat muun muassa erinomaiset ominaisuudet:

Se voi palvella sinua: Yhdistetty suhteellisuus: Selitys, kolme yhdistelmäsääntöä, harjoituksia

- Homotecia -keskus (O) on ainoa kaksoispiste ja se muuttuu itsensä; eli se ei vaihtele.

- Keskustan läpi kulkevista linjoista tulee itsensä (ne ovat kaksinkertaisia), mutta se muodostavat kohdat eivät ole kaksinkertaisia.

- Rivit, jotka eivät kulje keskustan läpi, muuttuvat yhdensuuntaisiksi viivoiksi; Tällä tavoin homotecia -kulmat pysyvät tasa -arvoisina.

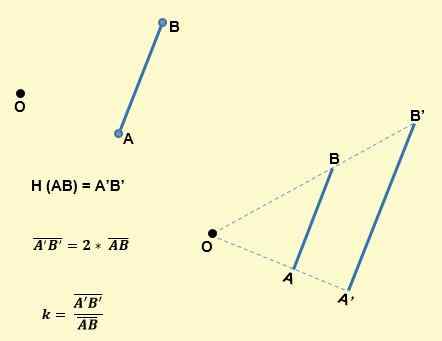
- Segmentin kuva keskikohdassa Homotecia tai ja syy K on sen yhdensuuntainen segmentti, ja sillä on k -kokoinen pituus. Esimerkiksi, kuten seuraavasta kuvasta nähdään, Homotecian AB -segmentti on toinen A'B -segmentti ', niin että AB on samansuuntainen A'B: n kanssa' ja K on:

- Homoteettiset kulmat ovat yhdenmukaisia; eli heillä on sama mitta. Siksi kulman kuva on kulma, jolla on sama amplitudi.

Toisaalta homotecia on vaihdettava sen syyn (k) arvosta riippuen, ja seuraavia tapauksia voi esiintyä:

- Jos vakio k = 1, kaikki kohdat ovat kiinteitä, koska ne muuttavat itsensä. Siten homotetinen hahmo osuu samaan aikaan alkuperäisen kanssa ja muutosta kutsutaan identiteettifunktioksi.

- Jos k ≠ 1, ainoa kiinteä piste on homotecian (o) keskipiste (O).

- Jos k = -1, homoteciasta tulee keskeinen symmetria (C); Eli kierto tapahtuu C: n ympärillä, 180 kulmassa^jompikumpi.

- Jos k> 1, muunnetun luvun koko on suurempi alkuperäisen koon suhteen.

Voi palvella sinua: Irrationaaliset numerot: historia, ominaisuudet, luokittelu, esimerkit

- Kyllä 0 < k < 1, el tamaño de la figura transformada será menor que el de la original.

- Kyllä -1 < k < 0, el tamaño de la figura transformada será menor y estará girada con respecto a la original.

- Kyllä k < -1, el tamaño de la figura transformada será mayor y estará girada con respecto a la original.

Homotecia -tyypit

Homotecia voitaisiin myös luokitella kahteen tyyppiin sen syyn arvosta riippuen: k):

Suora homotecia

Tapahtuu, jos vakio k> 0; Toisin sanoen homotetiikkapisteet ovat samalla puolella keskuksen suhteen:

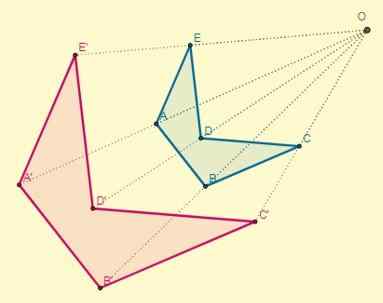
Suhteellisuuskerroin tai samankaltaisuussuhde suorien homotetisten lukujen välillä on aina positiivinen.

Käänteinen homotecia

Tapahtuu, jos vakio k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:

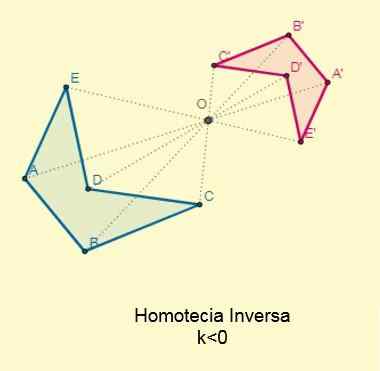
Käänteisten homotetisten lukujen välinen suhteellisuuskerroin tai samankaltaisuussuhde on aina negatiivinen.

Sävellys

Kun useita liikkeitä suoritetaan peräkkäin, kunnes alkuperäinen kuva on yhtä suuri, tapahtuu liikkeiden koostumus. Useiden liikkeiden koostumus on myös liike.

Kahden homotecian välinen koostumus johtaa uuteen homoteciaan; Toisin sanoen on homotecia -tuote, jossa keskus on linjassa kahden alkuperäisen muunnoksen keskipisteen kanssa, ja syy (k) on kahden syyn tuote.

Siten kahden koostumuksen koostumuksessa H₁(JOMPIKUMPI₁, k -k -₁) ja h₂(JOMPIKUMPI₂, k -k -₂), Syiden kertominen: k₁ x k₂ = 1 johtaa syyn h homoteciaan₃ = K₁ x k₂. Tämän uuden homotecian keskus (tai₃) sijaitsee linjalla tai₁ JOMPIKUMPI₂.

Se voi palvella sinua: vastakkaiset kulmat kärjen kautta (ratkaistu harjoitus)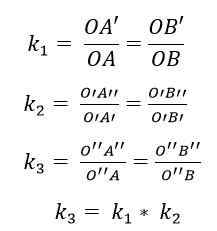

Homotecia vastaa tasaista ja peruuttamatonta muutosta; Jos sovelletaan kahta homoteciaa, joilla on sama keskus ja syy, mutta eri merkinnällä, alkuperäinen luku saadaan.

Homotecia -esimerkkejä

1. Ensimmäinen esimerkki

Levitä homotecia annettuun keskikeskuksen (O) monikulmioon, joka sijaitsee 5 cm: n päässä A: sta ja jonka syy on k = 0,7.

Ratkaisu

Mikä tahansa kohta on valittu Homotecian keskukseksi, ja tästä on vaihdettu kuvan kärkipisteet:

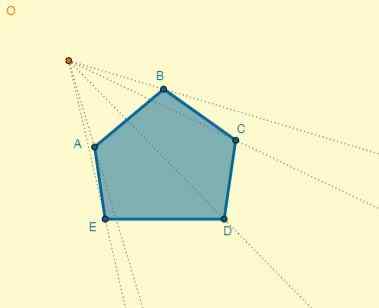
Etäisyys keskustasta (O) pisteeseen A on OA = 5; Tällä voit määrittää yhden homotetiikan pisteen etäisyyden (OA ') myös tietäen, että k = 0,7:

Oa '= k x oa.

OA '= 0,7 x 5 = 3,5.

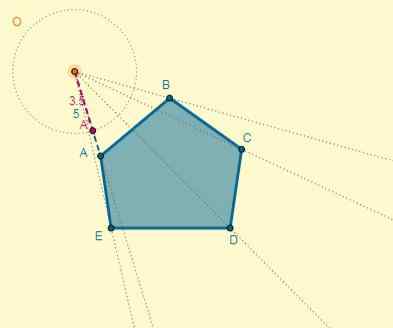
Prosessi voidaan tehdä jokaiselle kärkipisteelle tai voit myös piirtää homotetisen monikulmion muistaa, että kahdella monikulmiolla on yhdensuuntainen sivu:

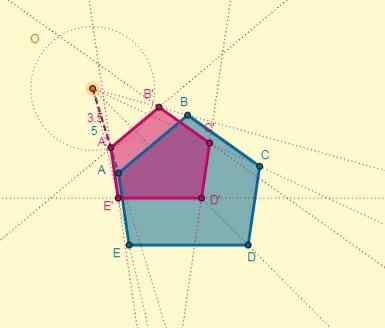
Lopuksi, muutos nähdään seuraavasti:

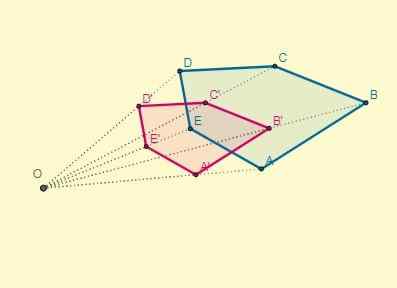
2. Toinen esimerkki

Levitä homotecia annettuun keskikeskuksen (O) monikulmioon, joka sijaitsee 8,5 cm: n päässä C: stä ja jonka ja syy K = -2.

Ratkaisu

Etäisyys keskustasta (O) pisteeseen C on OC = 8,5; Näiden tietojen avulla on mahdollista määrittää yhden homotetiikan pisteen etäisyys (OC '), tietäen myös, että k = -2:

Oc '= k x oc.

OC '= -2 x 8,5 = -17

Kun olet piirtänyt transformoidun monikulmion segmentit, alkuperäiset pisteet ja niiden homotetiikka sijaitsevat vastakkaisissa päissä keskustan suhteen: