Isometriset muutokset

Se isometriset muutokset Ne ovat tietyn luvun sijainnin tai suuntauksen muutoksia, jotka eivät muuta tämän muotoa tai kokoa. Nämä muunnokset luokitellaan kolmeen tyyppiin: käännös, kierto ja heijastus (isometria). Yleensä geometriset muunnokset sallivat uuden luvun luomisen toisesta.

Muutos geometriseksi hahmoksi tarkoittaa, että jollain tavalla se altistettiin jonkin verran muutoksille; eli sitä muutettiin. Alkuperäisen ja samanlaisen tason merkityksen mukaan geometriset muunnokset voidaan luokitella kolmeen tyyppiin: isometriset, isomorfiset ja anamorfiset.

Isometristen muunnosten ominaisuudet

- Isometriset muunnokset tapahtuvat, kun segmenttien ja kulmien suuruudet alkuperäisen kuvan ja transformoidun kuvan välillä säilytetään.

- Tämän tyyppisessä muunnoksessa kuvan muoto tai koko ei ole muuttunut (ne ovat yhteneviä), se on vain tämän sijainnin muutos joko suuntautumisessa tai mielessä. Tällä tavoin alkuperäinen luku ja finaali ovat samanlaisia ​​ja geometrisesti yhteneviä.

- Isometria viittaa tasa -arvoon; Eli geometriset luvut ovat isometrisiä, jos niillä on sama muoto ja koko.

- Isometrisissä muunnoksissa ainoa asia, joka voidaan havaita, on asemanvaihto tason, jäykkä liike tapahtuu, jonka lukumäärä kulkee alkuperäisestä sijainnista finaaliin. Tätä lukua kutsutaan alkuperäisen homologiseksi (samanlaiseksi).

- On olemassa kolmen tyyppisiä liikkeitä, jotka luokittavat isometrisen muunnoksen: käännös, kierto ja heijastus tai symmetria.

Isometristen muunnosten tyypit

Käännöksellä

Ovatko ne isometriat, jotka sallivat syrjäytymisen suorassa viivassa kaikki tason pisteet tiettyyn suuntaan ja etäisyyteen.

Kun kuva muuttuu käännöksellä, se ei muuta sen suuntausta suhteessa alkuperäiseen sijaintiin, eikä se menetä sisäisiä mittauksiaan, sen kulmien ja sivujen mitat. Tämäntyyppinen siirtymä määritetään kolmella parametrilla:

• Osoite, joka voi olla vaakasuora, pystysuora tai vino.
• Suunta, joka voi olla vasemmalle, oikealle, ylös tai alas.
• Etäisyys tai suuruus, joka on pituus, joka on alkuperäisestä asennosta minkä tahansa liikkuvan pisteen lopulliseen.

Voi palvella sinua: Curtory: Määritelmä, tyypit, kaavat, mitä se on esimerkiksi

Jotta isometrinen muunnos käännöksestä johtuu, sen on täytettävä seuraavat ehdot:

• Kuvion on aina pidettävä kaikki mitat, sekä lineaariset että kulmat.
• Kuva ei muuta sijaintiaan vaakasuoraan akseliin; eli sen kulma ei koskaan vaihtele.
• Käännökset on aina yhteenveto yhdessä, riippumatta tehtyjen käännösten lukumäärästä.

Tasossa, jossa keskus on piste tai koordinaattien kanssa (0,0), käännös määritetään vektorilla t (a, b), mikä osoittaa alkuperäisen pisteen siirtymisen. Tarkoittaen:

P (x, y) + t (a, b) = p '(x + a, y + b)

Esimerkiksi, jos koordinaattipistettä P (8, -2) käännös t (-4, 7) sovelletaan, se saadaan:

P (8, -2) + t (-4, 7) = p '[(8 + (-4)), ((-2) + 7)] = p' (4, 5)

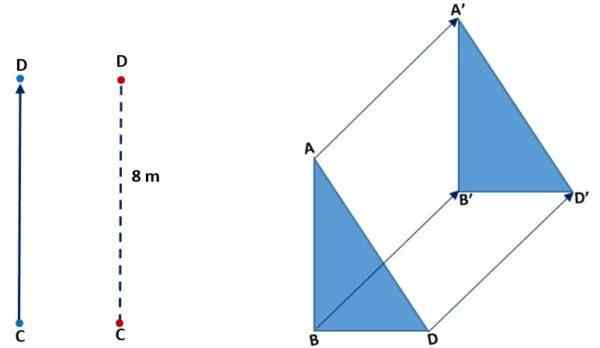
Seuraavassa kuvassa (vasen) näet kuinka piste C siirtyi samaan aikaan D: n kanssa. Hän teki sen pystysuoraan, merkitys nousi ja etäisyys tai suuruus CD oli 8 metriä. Oikeassa kuvassa havaitaan kolmion käännös:

Kierto

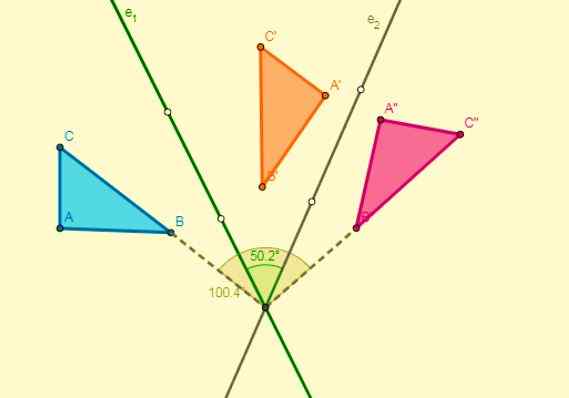
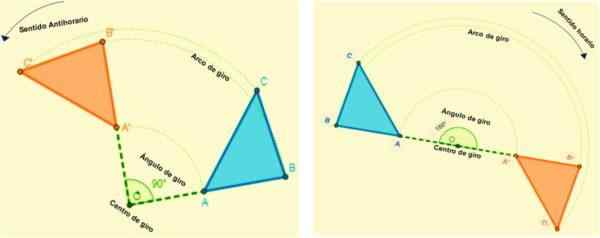
Ovatko ne isometriat, jotka antavat kuvan kääntää kaikki tason kohdat. Jokainen piste kääntyy kaaren seurauksena, jolla on vakiokulma ja kiinteä piste (kääntökeskus) määritetty.

Eli kaikki kierto määritellään sen pyörimis- ja kääntökulman keskuksen avulla. Kun kuva transformoituu pyörimällä, se ylläpitää kulmiensa ja sivujen mittaa.

Kierto tapahtuu tiettyyn suuntaan, se on positiivinen, kun käännös on anti -Horary (toisin kuin kellon kädet pyörivät) ja negatiivinen, kun sen käännös on myötäpäivään.

Jos pistettä (x, y) pyöritetään alkuperän suhteen -toisin sanoen sen pyörimiskeskus on (0,0) -90 kulmassa^jompikumpi 360^jompikumpi Pisteiden koordinaatit ovat:

Voi palvella sinua: Tilasto -oksat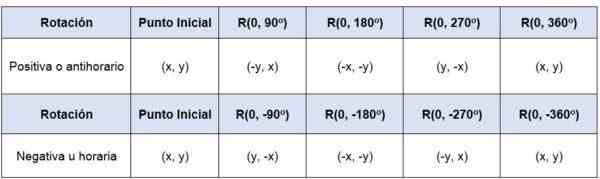

Siinä tapauksessa, että kierto ei ole lähtökohtana, koordinaattijärjestelmän alkuperä uuteen alkuperään on siirrettävä, jotta voidaan kiertää alkuperää olevaa keskustaa.

Esimerkiksi, jos piste P (-5,2) käytetään 90-kiertoa^jompikumpi, Alkuperä ja positiivisessa mielessä sen uudet koordinaatit ovat (-2,5).

Heijastuksella tai symmetrialla

Ovat ne muunnokset, jotka investoivat lentokoneen pisteitä ja lukuja. Tämä sijoitus voi olla pisteeseen tai voi olla myös linjan suhteen.

Toisin sanoen tämän tyyppisissä muunnoksissa jokainen alkuperäisen kuvan piste liittyy homologisen hahmon toiseen pisteeseen (kuva) siten, että piste ja sen kuva ovat samalla etäisyydellä linjasta, jota kutsutaan symmetria -akseliksi.

Siten kuvan vasen osa heijastaa oikeaa puolta muuttamatta sen muotoa tai mittoja. Symmetria muuttaa yhtä suuren kuvan, mutta päinvastoin, kuten seuraavassa kuvassa voidaan nähdä:

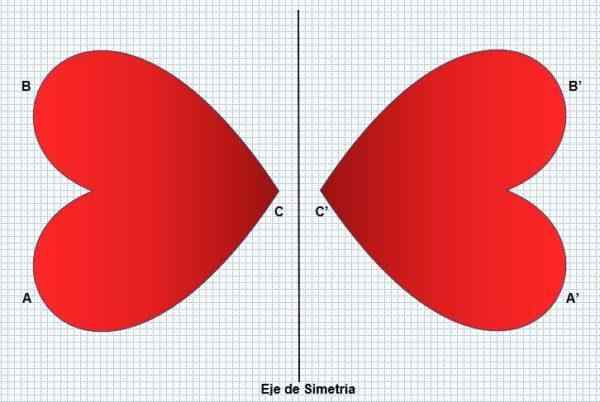
Symmetria on läsnä monilla näkökohdilla, kuten jotkut kasvit (auringonkukka), eläimet (riikinkukko) ja luonnonilmiöt (lumihiutaleet). Ihminen heijastaa sitä hänen kasvonsa, jota pidetään kauneustekijänä. Heijastus tai symmetria voi olla kahta tyyppiä:

Keskeinen symmetria

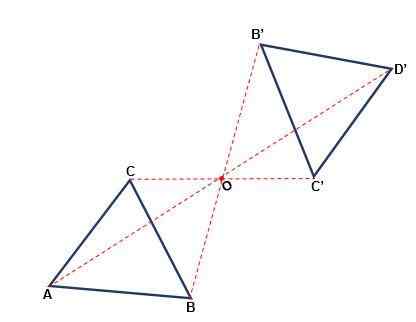
Se on se, joka tapahtuu pisteeseen nähden, jossa kuva voi muuttaa sen suuntausta. Jokainen alkuperäisen kuvan ja sen kuvan piste on samalla etäisyydellä pisteestä tai nimeltään symmetriakeskus. Symmetria on keskeinen, kun:

• Sekä kohta että sen kuva että keskusta kuuluvat samaan linjaan.
• Kierto 180^jompikumpi Keskustasta tai alkuperäisestä yhtä suuresta kuvasta saadaan.
• Alkukuvion aivohalvaukset ovat yhdensuuntaiset muodostetun kuvan iskujen kanssa.
• Kuvan merkitys ei muutu, se on aina aikataulussa.

Voi palvella sinua: kuinka paljon sinun on lisättävä 3/4 saadaksesi 6/7?

Aksiaalinen symmetria

Tämä muunnos tapahtuu symmetria -akselin suhteen, jossa jokainen alkuperäisen kuvan piste liittyy kuvan toiseen pisteeseen ja nämä ovat samalla etäisyydellä kuin symmetria -akseli. Symmetria on aksiaalinen, kun:

• Segmentti, joka liittyy kuvaan sen kuvaan, on kohtisuorassa symmetria -akseliinsa nähden.
• Luvut muuttavat niiden merkitystä käännös- tai aikasuunnassa.
• Jakamalla kuva keskuslinjalla (symmetria -akseli), yksi tuloksena olevista puolikkaista on täysin toisen puolikkaiden kanssa.

Sävellys

Isometrinen muunnoskoostumus viittaa isometristen muunnosten peräkkäiseen soveltamiseen samassa luvussa.

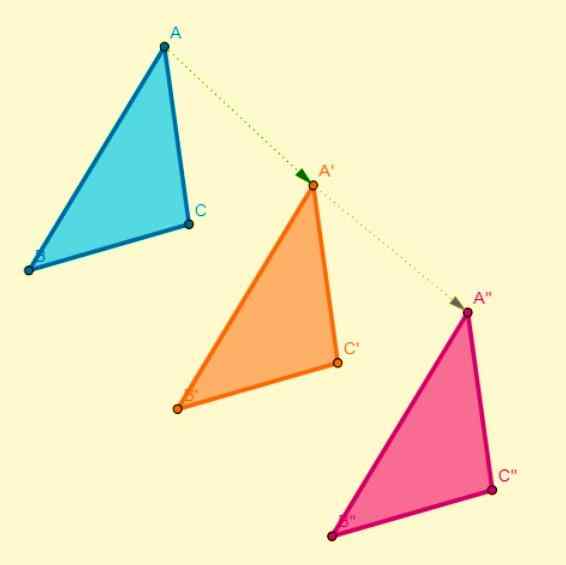
Käännöksen koostumus

Kahden käännöksen koostumus johtaa toiseen käännökseen. Kun tasossa suoritetaan, vaaka -akselilla (x) vain kyseisen akselin koordinaatit muuttuvat, kun taas pystysuoran akselin (y) koordinaatit pysyvät samana ja päinvastoin.

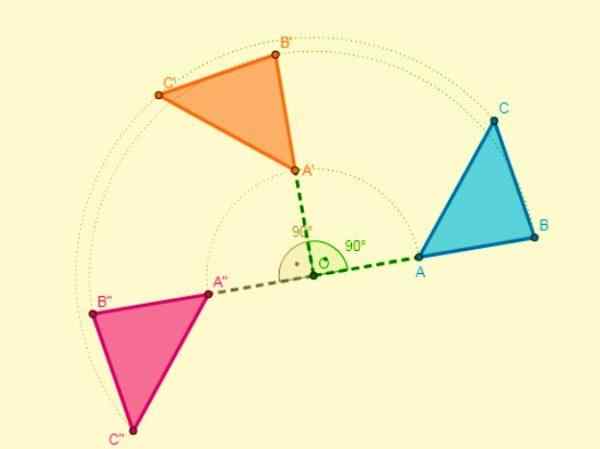
Kiertokoostumus

Kahden käännöksen koostumus samaan keskukseen johtaa toiseen käännökseen, jolla on sama keskus ja jonka amplitudi on kahden käännöksen amplitudien summa.

Jos keskustassa on erilainen keskusta, samankaltaisten pisteiden kahden segmentin leikkaus on pyörimiskeskus.

Symmetrian koostumus

Tässä tapauksessa koostumus riippuu siitä, miten sitä käytetään:

• Jos samaa symmetriaa sovelletaan kahdesti, tulos on identiteetti.
• Jos kahta rinnakkaista akselia käytetään kahta symmetriaa, tulos on translaatio ja niiden siirtymä on kaksinkertainen näiden akselien etäisyyteen:

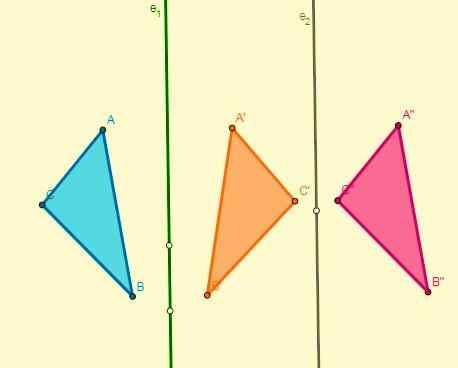
• Jos kahta symmetriaa käytetään suhteessa kahteen akseliin, jotka leikataan pisteeseen O (keskellä), saadaan kierto keskipisteellä ja sen kulma on kaksinkertainen kulmaan, jonka akselit muodostuvat: