Pythagorean -identiteettiesittely, esimerkki, harjoitukset

Are Pythagorean -identiteetti Kaikki trigonometriset yhtälöt, jotka täyttyvät minkä tahansa kulman arvon suhteen ja perustuvat Pythagoras -lauseen. Kuuluisin Pythagorean -identiteetistä on trigonometrinen perustavanlaatuinen identiteetti:

Senttiä²(α) + cos²(α) = 1

Kuvio 1. Pythagorean trigonometrinen identiteetti.

Se on edelleen tärkeä ja käyttää tangentin ja secantin Pythagoran identiteettiä:

Niin²(α) + 1 = s²(α)

Ja Pythagoran trigonometrinen identiteetti, johon sisältyy kotangentti ja harvesteri:

1 + CTG²(α) = CSC²(α)

[TOC]

Esittely

Trigonometriset syyt rinta ja kosini Ne on edustettuna säteen ympärysmitalla yksi (1), joka tunnetaan nimellä trigonometrinen ympyrä. Tällä ympyrällä on keskusta koordinaattien alkuperässä tai.

Kulmat mitataan X: n positiivisesta puoliakselista, esimerkiksi kulma α kuviossa 2 (katso myöhemmin). Vastoin kellon käsiä, jos kulma on positiivinen, ja käsien suuntaan, jos se on negatiivinen kulma.

Puoli -oikea alkuperän tai ja kulma α on piirretty, mikä sieppaa yksikköympyrän pisteessä P. Piste P projisoidaan ortogonaalisesti vaaka -akselilla x, joka antaa pisteeseen C. Samoin P projisoidaan kohtisuoraan pystysuoralla akselilla ja aiheuttaen pistettä S.

Sinulla on oikea OCP -kolmio C: ssä. 

Rinta ja kosiini

On muistettava, että trigonometrinen syy rinta Se on määritelty oikealla kolmiolla seuraavasti:

Kolmion kulman rinta on suhde tai suhde Cateton välillä vastustaa kolmion kulmaa ja hypotenusia.

Sovellettu kuvan 2 OCP -kolmioon olisi tällainen:

Sin (α) = cp / op

Mutta cp = OS ja OP = 1, niin että:

Synti (α) = OS

Mikä tarkoittaa, että Y -akselin projektiolla on arvo, joka on yhtä suuri kuin esitetyn kulman rinta. On huomattava, että kulman (+1) rinnan maksimiarvo tapahtuu, kun α = 90º ja minimi (-1), kun α = -90º tai α = 270º.

Voi palvella sinua: vektoritila: pohja ja mitta, aksioomit, ominaisuudet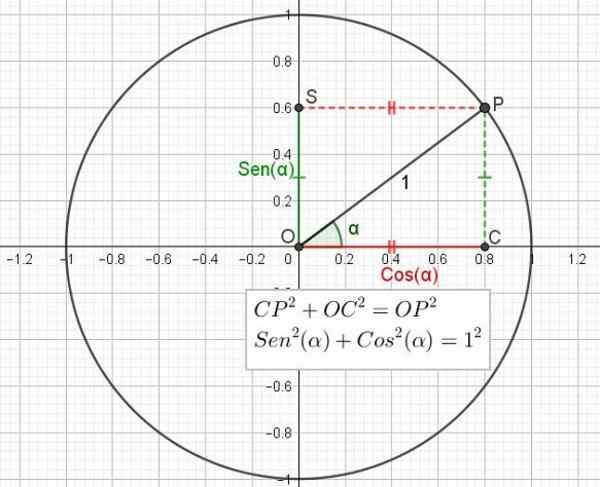Kuva 2. Trigonometrinen ympyrä, joka osoittaa Pythagoras -lauseen ja perustavanlaatuisen trigonometrisen identiteetin välisen suhteen. (Oma yksityiskohta)

Samoin kulman kosiini on suhde kulman vieressä olevan luokan ja kolmion hypotenuusin välillä.

Sovellettu kuvan 2 OCP -kolmioon olisi tällainen:

Cos (α) = OC / OP

Mutta op = 1, niin että:

Cos (α) = OC

Mikä tarkoittaa, että X -akselin OC -projektiolla on arvo, joka on yhtä suuri kuin esitetyn kulman rinta. On huomattava, että kosinin (+1) maksimiarvo tapahtuu, kun α = 0º tai α = 360º, kun taas kosinin minimiarvo on (-1), kun α = 180º.

Perus identiteetti

Suorakulmion OCP -kolmiolle sovelletaan Pythagoras -lause, joka toteaa, että luokkien neliön summa on yhtä suuri kuin hypotenusen neliö:

CP² + Oc² = OP²

Mutta on jo sanottu, että CP = OS = sin (α), että OC = cos (α) ja että OP = 1, joten edellinen lauseke voidaan kirjoittaa uudelleen kulman sinus- ja kosinusta riippuen:

Senttiä²(α) + cos²(α) = 1

Tangentti -akseli

Aivan kuten trigonometrisen ympyrän X -akseli on kosinin ja akselin ja rinnan akselin akseli, samalla tavalla on tangentin akseli (katso kuva 3), joka on juuri yksikön tangentti viiva Ympyrä pisteessä B -koordinaatissa (1, 0). 

Jos haluat tietää kulman tangentin arvon, kulma vedetään X: n positiivisesta puoliakselista, kulman leikkauskohta tangentin akselin kanssa määrittelee pisteen Q, OQ -segmentin pituus on kulman tangentti.

Voi palvella sinua: algebralliset johdannaiset

Tämä johtuu siitä, että määritelmän mukaan kulman α tangentti on päinvastainen Cateto QB viereisen cateto OB: n välillä. Toisin sanoen niin (α) = qb / ob = qb / 1 = qb.

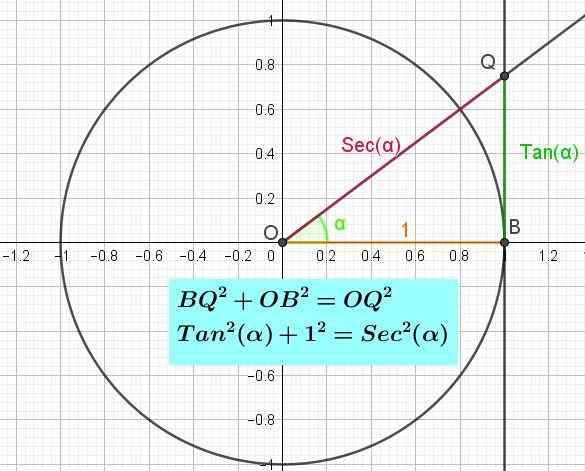Kuva 3. Trigonometrinen ympyrä, joka näyttää tangentin akselin ja tangentin pythagoran identiteetin. (Oma yksityiskohta)

Tangentin pythagoran identiteetti

Tangentin pythagoran identiteetti voidaan osoittaa, jos suorakulmiokolmio B: ssä (kuva 3) otetaan huomioon (kuva 3). Pythagoras -lauseen soveltaminen mainitulle kolmiolle, sinun on bq² + Ob² = OQ². Mutta on jo sanottu, että bq = tan (α), että OB = 1 ja että OQ = SEC (α), niin että oikean kolmion obq: n Pythagoras -tasa -arvon korvaaminen on:

Niin²(α) + 1 = s²(α).

Esimerkki

Varmista, täyttyykö Pythagorean -identiteetit Catetos AB = 4: n suorakulmiokolmiossa vai ei.

Ratkaisu: Luokat tunnetaan, on välttämätöntä määrittää hypotenuse, joka on:

Ac = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Kulmaa ∡BAC kutsutaan α, ∡bac = α. Nyt trigonometriset syyt määritetään:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = BC / AB = 3/4 

Cotan α = ab / bc = 4/3 

SEC α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Se alkaa trigonometrisellä identiteettillä:

Senttiä²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Päätelee, että se täyttyy.

- Seuraava Pythagoran identiteetti on tangentti:

Niin²(α) + 1 = s²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

Ja päätellään, että tangentin identiteetti varmistetaan.

- Samoin kotangentin:

Voi palvella sinua: Satunnaiset valinnat korvaavan tai ilman

1 + CTG²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Päätelmä on myös toteutunut, mikä on suorittanut tehtävän tarkistaa Pythagorean -identiteetit annetulle kolmiolle.

Ratkaisut

Testaa seuraavat identiteetit trigonometristen syiden ja pytagorisen identiteetin määritelmien perusteella.

Harjoitus 1

Todista mitä cos² x = (1 + sen x) (1 - sin x).

Ratkaisu: Oikea jäsen tunnistaa merkittävän tuotteen binomiaalin kertolaskusta sen konjugaatin avulla, joka, kuten tiedetään, on neliöiden ero:

Koos² x = 1² - Senttiä² x

Sitten termi, jolla on oikea oikealla puolella, kulkee vasemmalle puolelle muutettua merkkiä:

Koos² X + Sen² x = 1

Huomaa, että perustavanlaatuinen trigonometrinen identiteetti on saavutettu, joten päätellään, että annettu ilmaisu on identiteetti, ts. Se täyttyy minkä tahansa arvon x: n arvoon.

Harjoitus 2

Alkaen perusteellisesta trigonometrisestä identiteetistä ja trigonometristen syiden määritelmien käyttäminen Harvesterin pythagoran identiteetin osoittamiseksi.

Ratkaisu: Perus identiteetti on:

Senttiä²(x) + cos²(x) = 1

Molemmat jäsenet on jaettu senin kesken²(x) ja nimittäjä on jaettu ensimmäiseen jäseneen:

Senttiä²(x)/synti²(x) + cos²(x)/synti²(x) = 1/Sen²(x)

Sitä yksinkertaistetaan:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) on identiteetti (ei -pytthagorinen), joka varmistetaan trigonometristen syiden määritelmällä. Samalla tavalla se tapahtuu seuraavalla identiteettillä: 1/sin (x) = csc (x).

Lopuksi sinun täytyy:

1 + CTG²(x) = csc²(x)

Viitteet

1. Baldor J. (1973). Litteä geometria ja tila, jossa on johdanto trigonometriaan. Keski -Amerikan kulttuuri-. C.-Lla.
2. C. JA. -Lla. (2003). Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
3. Campos, f., Cerecedo, f. J -. (2014). Matematiikka 2. Patria -toimitusryhmä.
4. Iger. (S.F.-A. Matematiikka ensimmäisen lukukauden Tacaná. Iger.
5. Jr. Geometria. (2014). Monikulmio. Lulu Press, Inc.
6. Miller, Heeren ja Hornsby. (2006). Matematiikka: Perustelu ja sovellukset (kymmenes painos). Pearson -koulutus.
7. Patiño, m. (2006). Matematiikka 5. Toimitusohjelma.
8. Wikipedia. Trigonometrian identiteetit ja kaavat. Palautettu: on.Wikipedia.com