Konvergenssilinssin ominaisuudet, tyypit ja liikunta ratkaistu

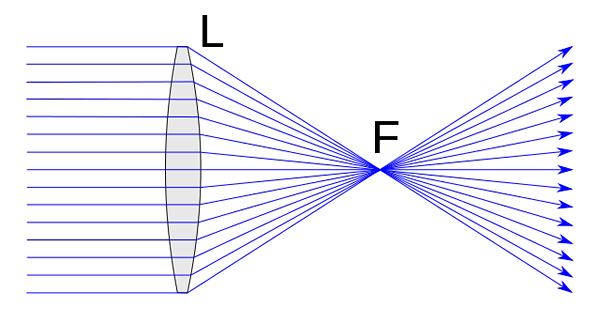
Se Konvergenssilinssit Ne ovat ne, jotka ovat paksumpia keskellä ja ohuemmassa osassaan reunoilla. Seurauksena on, että ne keskittyvät (konvergoivat) yhdessä pisteessä valonsäteet, jotka vaikuttavat heihin pääakselin suuntaisesti. Tätä kohtaa kutsutaan Focus- tai kuvan tarkennukseksi, ja sitä esitetään kirjaimella F. Konvergenssit tai positiiviset linssit muodostavat niin kutsutut objektien todelliset kuvat.

Tyypillinen konvergenssi linssiesimerkki on suurennuslasi. On kuitenkin yleistä löytää tämän tyyppisiä linssejä paljon monimutkaisemmista laitteista, kuten mikroskoopista tai kaukoputkista. Itse asiassa emäksinen yhdisteiden mikroskooppi on se, joka muodostuu kahdesta konvergenssista linssistä, joilla on pieni polttoväli. Näitä linssejä kutsutaan kohteeksi ja silmä.

Suurennuslasi, konvergenssi linssi. 

Konvergenssilinssejä käytetään optiikassa eri sovelluksiin. Siten niiden on osoitettu käsittelemään.

[TOC]

Ominaisuudet

Konvergenssi linssi. Chetvorno [CC0]

Konvergenssilinssillä on sarjan ominaisuudet, jotka määrittelevät ne. Joka tapauksessa ehkä tärkein on se, mitä olemme jo edenneet sen määritelmässään. Siten lähentyviä linssejä on ominaista ohjaamalla keskittymisen läpi kaikki säteet, jotka vaikuttavat niihin pääakselin suuntaiseen suuntaan.

Lisäksi vastavuoroisesti mikä tahansa painopiste läpäisevä tapaussäte tai taittuu linssin optisen akselin suuntaisesti.

Konvergenssilinssien elementit

Tutkimuksesi edessä on tärkeää tietää, mitkä elementit muodostavat linssit yleensä ja erityisesti konvergenssit.

Yleensä sitä kutsutaan linssin optiseksi keskukseksi pisteeseen, jolla jokainen sen läpi kulkeva säde ei koe poikkeamaa.

Pääakseli on linja, joka liittyy optiseen keskukseen ja pääpainopisteeseen, jonka olemme jo kommentoineet, jotka on esitetty kirjaimella F.

Voi palvella sinua: Ton: Muutokset, vastaavuudet ja harjoitukset ratkaistu

Sitä kutsutaan pääpainoksi pisteeseen, jossa kaikki säteet, jotka vaikuttavat linssiin pääakselin kanssa.

Optisen keskuksen ja tarkennuksen välistä etäisyyttä kutsutaan polttovälin etäisyydelle.

Kaarevuuskeskukset määritellään linssin luomien pallokeskuksiksi; Toisaalta objektiivien kaarevuusradioiden radiot, jotka aiheuttavat linssiä.

Ja lopuksi sitä kutsutaan optiseksi tasoksi linssin keskustasoon.

Kuvien muodostuminen konvergenssissa linsseissä

Kuvien muodostumisen yhteydessä konvergensseihin.

Jos säde vaikuttaa linssiin akselin suuntaisesti, nouseva säde lähenee tarkennuskuvaa. Käänteisesti, jos tapahtuva säde ylittää esineen keskittymisen, salama nousee akselin suuntaiseen suuntaan. Lopuksi, optisen keskuksen ylittävät säteet taiputetaan ilman poikkeamia.

Seurauksena on, että lähentävässä linssissä voit antaa seuraavat tilanteet:

- Että objekti sijaitsee suhteessa optiseen tasoon etäisyydellä, joka on yli kaksinkertainen polttovälin etäisyydellä. Tällöin esiintyvä kuva on todellinen, käänteinen ja pienempi kuin esine.

- Että objekti sijaitsee etäisyydellä optisesta tasosta, joka on yhtä suuri kuin kaksinkertainen polttoetäisyys. Kun tämä tapahtuu, saatu kuva on todellinen, käänteinen kuva ja samankokoinen kuin esine.

- Että objekti on etäisyydellä optisesta tasosta kerran ja kahdesti polttovälin etäisyydellä. Joten kuva on tuotettu todellinen, käänteinen ja suurempi kuin alkuperäinen objekti.

- Että objekti sijaitsee etäisyydellä optisesta tasosta, joka on alempi kuin polttoväli. Tällöin kuva on virtuaalinen, suora ja suurempi kuin objekti.

Voi palvella sinua: magneettinen sokki: yksiköt, kaavat, laskenta, esimerkit

Konvergenssilinssityypit

Konvergenssilinssejä on kolme erityyppistä.

Biconvex -linssit, kuten nimestä päätetään, koostuu kahdesta kuperasta pinnasta. Sillä välin planoconvexasilla on tasainen pinta ja toinen kupera. Ja lopuksi, koverokokoiset linssit muodostavat hiukan koveran pinnan ja toisen kuperan.

Ero erilaisissa linsseissä

Konvergenssi linssi. Fir0002 (keskustelu) (lataukset) [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Toisaalta erilaiset linssit eroavat konvergenssista siinä mielessä, että paksuus vähenee reunoista kohti keskustaa. Siten, toisin kuin konvergenssin kanssa tapahtui, tämän tyyppisissä linsseissä valonsäteet, jotka vaikuttavat pääakseliin rinnakkain. Tällä tavoin ne muodostavat niin kutsutut objektien virtuaaliset kuvat.

Optiikassa erilaiset tai negatiiviset linssit, kuten myös tunnetaan, käytetään pääasiassa likinäköisyyden korjaamiseen.

Gauss -ohuiden linssien yhtälöt ja lisääntynyt linssi

Yleensä tutkittujen linssien tyyppi on niitä, joita kutsutaan ohuiksi linsseiksi. Nämä määritellään sellaisiksi, joilla on pieni paksuus verrattuna niiden rajoittavien pintojen kaarevuuteen.

Tämän tyyppistä linssiä voidaan tutkia Gauss -yhtälön ja yhtälön kanssa, joka mahdollistaa linssin kasvun määrittämisen.

Gauss -yhtälö

Ohujen linssien Gauss -yhtälö aikoo ratkaista monien perusoptiikkaongelmien ratkaisemisen. Siksi sen suuri merkitys. Ilmaisusi on seuraava:

1/f = 1/p +1/Q

Missä 1/ F on ns. Linssin voimana ja F on polttoväli tai etäisyys optisesta keskustasta fokusan. Linssin tehon mittayksikkö on diopteri (D), joka on 1 d = 1 m^-1. Puolestaan ​​P ja Q ovat vastaavasti etäisyys, jolla objekti ja etäisyys, johon sen kuva havaitaan.

Se voi palvella sinua: Big Bang -teoria: Ominaisuudet, vaiheet, todisteet, ongelmat

Lisääntynyt linssi

Ohut linssin sivuttainen lisäys saadaan seuraavalla lausekkeella:

M = - q / p

Missä m on lisäys. Kasvun arvosta voidaan päätellä sarja seurauksia:

Kyllä | M | > 1, kuvan koko on suurempi kuin objekti

Kyllä | M | < 1, el tamaño de la imagen es menor que el del objeto

Jos m> 0, kuva on oikea ja samalla puolella objekti (virtuaalinen kuva)

Kyllä m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Liikuntaa

Runko sijaitsee metrin päässä konvergenssista linssistä, jonka polttoväli on 0, 5 metriä. Millainen kehon kuva on? Kuinka pitkälle löydät?

Meillä on seuraavat tiedot: p = 1 m; F = 0,5 m.

Korvaamme nämä arvot ohuiden linssien Gauss -yhtälössä:

1/f = 1/p +1/Q

Ja seuraava pysyy:

1/0,5 = 1 + 1/Q; 2 = 1 + 1/Q

Puhdistamme 1/q

1/Q = 1

Sitten puhdistaa Q ja hankkia:

Q = 1

Sieltä korvaamme linssin lisääntymisen yhtälössä:

M = -q / p = -1 / 1 = -1

Siksi kuva on todellinen, koska q> 0, käänteinen, koska m < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Viitteet

1. Valo (n.d -d.-A. Wikipediassa. Haettu tästä 18. maaliskuuta 2019.Wikipedia.org.
2. Lekner, John (1987). Heijastusteoria, sähkömagneettiset ja parisuhteet. Jousto.
3. Valo (n.d -d.-A. Wikipediassa. Haettu 20. maaliskuuta 2019,.Wikipedia.org.
4. Linssi (n.d -d.-A. Wikipediassa. Haettu tästä 17. maaliskuuta 2019.Wikipedia.org.
5. Linssi (optiikka). Wikipediassa. Haettu 19. maaliskuuta 2019,.Wikipedia.org.
6. ACTS, Eugene (2002). Optiikka (4. ed.-A. Addison Wesley.
7. Tupler, Paul Allen (1994). Fyysinen. Kolmas painos. Barcelona: Käännyin.