Ampère -kaava ja yhtälöiden laki, esittely, harjoitukset

Se Ampère -laki toteaa, että magneettisen induktiovektorin kierto B - Se on verrannollinen voimakkuuteen ja virtaan, joka virtaa samalla.

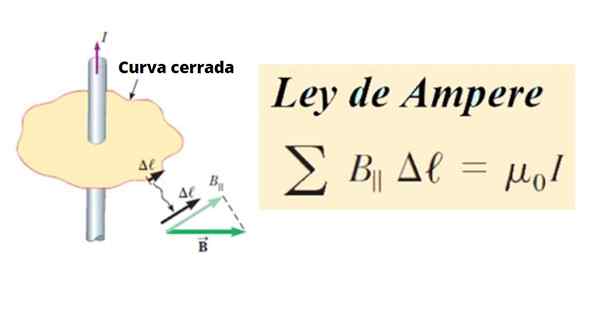
Vuorostaan ​​kierto B - Se on kaikkien tuotteiden summa tangentiaalisen komponentin B välillä_║ ja pienen segmentin pituus Δℓ suljetun käyrän C, Piirin ympärillä. Matemaattisesti se on kirjoitettu näin:

∑ b_║ .Δℓ ∝ Yllyttää

Kuvio 1. Määritelmä ampeerilaki. Lähde: Serway, R. Korkeakoulufysiikka.

Mielivaltaisena viivana tai käyränä se voidaan jakaa pieniin segmentteihin Δℓ, Ja nämä puolestaan ​​voivat olla äärettömiä, niin niitä kutsutaan Dℓ.

Tässä tapauksessa summasta tulee skalaarituotteen olennainen viiva vektorien välillä B - ja Ds. Tämä tuote sisältää B: n tangentiaalisen komponentin, joka on B cosθ, missä θ on vektorien välinen kulma:

Integraalin ylittävä pieni ympyrä tarkoittaa, että integraatio suoritetaan suljetulla tiellä C, joka tässä tapauksessa käsittää kuljettajan poikkileikkauksen läpi virtaavan virran.

Tasa -arvon määrittämiseksi tarvittava suhteellisuusvakio on μ_jompikumpi, Tyhjiöläpäisevyys. Tällä tavoin Ampèren laki on edelleen:

Ampèren laki kertoo meille, että linja olennainen ∫_C B - ∙ Ds Se on tarkalleen μ arvoinen_jompikumpiMinä, mutta se ei tarjoa meille yksityiskohtia siitä, kuinka magneettikenttä on suunnattu B - Käyrän C suhteen jokaisessa pisteessä tai siitä, miten integraali lasketaan. Se kertoo meille vain, että sen tulos on aina μ_jompikumpiYllyttää.

[TOC]

Ampèren lain osoittaminen

Ampèren laki varmennetaan kokeellisesti tarkistamaan erittäin pitkän läpimenoksen tuottaman magneettikentän. Ennen ongelman ratkaisemista on korostettava kaksi erityistä kiinnostavaa tapausta edellisestä yhtälöstä:

Se voi palvella sinua: valoisat elimet: ominaisuudet ja kuinka ne tuottavat oman valonsa

-Ensimmäinen on milloin B - ja Ds Ne ovat yhdensuuntaisia, mikä tarkoittaa sitä B - on tangentiaalinen C: lle. Sitten molempien vektoreiden välinen kulma on 0º ja skalaarituote on yksinkertaisesti suuruuksien tuote B -.ds.

-Toinen tapahtuu, jos B - ja Ds Ne ovat kohtisuorassa, jolloin skalaarituote on 0, koska vektorien välinen kulma on 90º, jonka kosiini on 0.

Toinen tärkeä yksityiskohta on käyrän C valinta, jolla kentän kierto arvioidaan. Ampèren laissa ei täsmennetä mitä se voi olla, mutta sen on käärittävä nykyinen jakauma. Se ei myöskään sano, kuinka käyrä matkustaa ja tälle on kaksi mahdollisuutta.

Ratkaisu on osoittaa merkkejä oikean peukalon säännön mukaisesti. Neljä sormea ​​ovat kaarevat siihen suuntaan, johon haluat integroida, yleensä tämä on sama kentällä B - kiertää. Jos nykyiset pisteet oikean peukalon suuntaan, merkki osoitetaan ja jos ei, merkki -.

Tämä pätee, kun jakauma on useiden virtojen kanssa, jotkut voivat olla positiivisia ja muita negatiivisia. Niiden algebrallinen summa on se, mitä aiomme asettaa Ampèren lakiin, joka yleensä nimitetään Kestämätön virta (Käyrälle C).

Strektilinan ja äärettömän langan magneettikenttä

Kuvio 2 esittää langan, joka kuljettaa virran ja ulos tasosta. Oikea peukalosääntö varmistaa sen B - Se kiertää vastakkaiseen suuntaan ja kuvaa ympärysmiiviä, kun punaiset nuolet osoittavat.

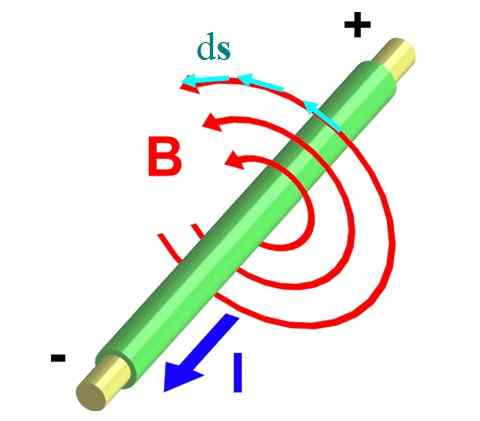Kuva 2.- Äärettömän langan magneettikenttä. Lähde: Wikimedia Commons.

Otetaan yksi heistä, jonka säde on r. Jaamme sen pieniksi differentiaalisegmenteiksi ds, edustaa siniset vektorit. Molemmat vektorit, B - ja Ds, Ne ovat yhdensuuntaisia ​​kehän jokaisessa pisteessä ja tällä tavalla integraali ∫_C B - ∙ Ds Se muuttuu:

Voi palvella sinua: Suoravirta

∫_C Bds

Tämä johtuu siitä, että kuten aiemmin totesimme, skalaarituote B - ∙ Ds  Se on vektoreiden suuruuksien tuote 0º kosinulla. Integraalin tulos tunnetaan Ampèren lain ansiosta, joten kirjoitamme:

∫_C BDS = μ_jompikumpiYllyttää

Koska kentän suuruus on vakio koko radan ajan, se jättää integraalin:

B ∫_C DS = μ_jompikumpiYllyttää

Integraali ∫_C DS edustaa kaikkien äärettömien pienten segmenttien summaa, jotka muodostavat radion ympärysmiipan r -, Vastaa sen pituutta, sen säteen tuote 2π:

B -.2πr = μ_jompikumpiYllyttää

Ja sieltä havaitaan, että B: n suuruus on:

B = μ_jompikumpiI / 2πr

On välttämätöntä korostaa, että vaikka valittu suuntaus (tai Amperian piiri) Ei pyöreä, integraalin tulos on edelleen μ_jompikumpiMinä, vaikka ∫_C B - ∙ Ds Se ei enää olisi b.2πr.

Siksi Ampèren lain hyödyllisyys magneettikentän määrittämisessä on jakaumien valitseminen korkealla symmetrialla siten, että integraali on helppo arvioida. Pyöreä ja suoraviivainen suuntaus täyttävät tämän vaatimuksen.

Ratkaisut

- Harjoitus 1

Harkitse käyriä A, B, C ja D esitetty kuvassa 3. He käärivät kolme virtaa, kaksi, jotka poistuvat tasosta, symboloivat yhdellä pisteellä ( . ), jonka voimakkuudet ovat 1 a ja 5 a, ja virta, joka tulee tasolle, joka on merkitty ristillä ja jonka suuruus on 2 a.

Etsi jokainen käyrä.

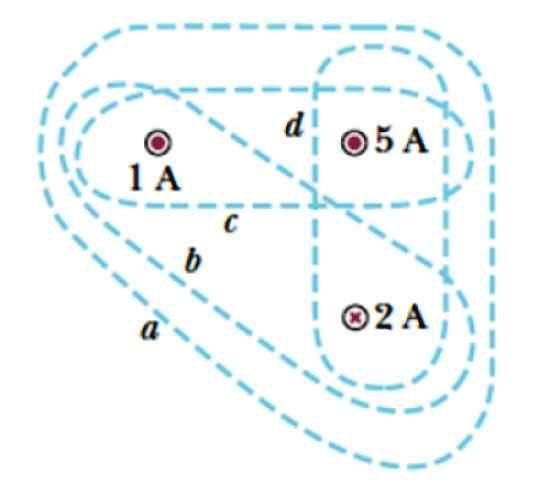Kuva 3. Useita käyriä Ampèren lain soveltamiseksi. Lähde: Serway, R. Korkeakoulufysiikka.

Ratkaisu

Paperille jättäville virroille on osoitettu merkki +. Tämän perusteella:

Se voi palvella sinua: pinnalliset aallot: ominaisuudet, tyypit ja esimerkit

Käyrä a

Suljetaan kolme virtaa, joten suljettu virta on + 1 A + 5 A - 2 A = 4 A.

Käyrä B

Vain 1 a y - 2 a: n virrat ovat tämän käyrän sisällä, joten suljettu virta on osoitteesta - 2 a.

Käyrä c

Sisältää lähtevät virrat 1 ja 5 a, joten suljettu virta on 6 a.

Käyrä d

Sisällä olevat virrat ovat +5 a ja - 2 a, sitten sulkevat verkkovirran 3 -.

- Harjoitus 2

Laske magneettikentän suuruus, joka on tuotettu erittäin pitkällä suoraviivaisella johdolla.

Ratkaisu

Ampèren lain mukaan lankakenttä antaa:

B = μ_jompikumpiI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 6. Sähkömagnetismi. Toimittanut Douglas Figueroa (USB).
2. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa.  Pearson.
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Nide 2.
4. Serway, R. 2009. Korkeakoulufysiikka. Cengage -oppiminen.
5. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Nide 2. Toimitus palautti.