Biot-Savart Law Formula, esittely, sovellukset, harjoitukset

Se Biot-Savart -laki muodostaa suhteen magneettikentän D välilläB -  Kohdassa P, tuotettu ohut lanka, joka kuljettaa virran I ja jonka differentiaalipituus on Ds. Tätä lakia käytetään nykyisten jakautumisten magneettikentän läpi Superpositioperiaate. 

Tämä tarkoittaa, että kokonaismagneettikentän laskemiseksi pisteessä P on lisättävä kaikki panokset, jotka jokainen differentiaaliosa Ds langan myötävaikuttaa. Ja tämä summa tehdään koko nykyisen jakauman kautta suoritetulla integraalilla.

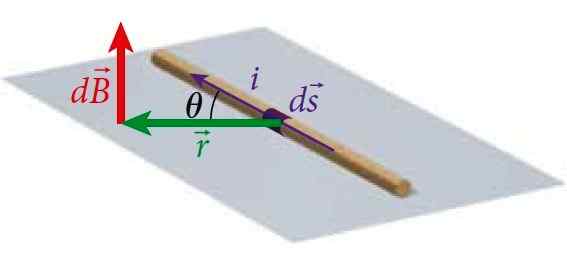
Kuvio 1. Lankasegmentti kuljettaa virran I, joka tuottaa magneettikentän pisteessä P tietyllä etäisyydellä langasta, joka on laskettu biot-savalalla. Lähde: Bauer, W. Fysiikka tekniikkaan ja tieteisiin.

Tällä tavalla voit laskea kentän, joka tuottaa johtoja eri geometrioiden virralla.

Biot-Savartin laki on nimetty kahden ranskalaisen fyysikon mukaan, jotka löysivät sen vuonna 1820: Jean Marie Biot (1774-1862) ja Felix Savart (1791-1841). Tämän saavuttamiseksi heidän oli tutkittava lukuisten virran jakaumien tuottaman magneettikentän voimakkuus ja muoto.

[TOC]

Kaava

Biot-Savart-lain matemaattinen ilmaisu on seuraava:

Se ylläpitää analogioita vastaavan sähkökentän laskemisen kanssa: Coulombin laki, vain että magneettikenttä DB - P on kohtisuorassa koneeseen, jossa lanka sijaitsee. Voimme nähdä tämän kuvassa 1.

Aikaisempi ilmaisu voidaan kirjoittaa myös seuraavasti:

Molemmissa ilmaisuissa, r - Se on sijaintivektori, joka on suunnattu ID -virran elementistäs siihen pisteeseen, että haluat laskea kentän.

Voi palvella sinua: lineaarisen vauhdin säilyttäminen: periaate, esimerkit, harjoitukset.

Omalta osaltaan, r - Ympyrä -aksentilla on yhtenäinen vektori, joka on suunnattu samaan suuntaan ja suuntaan, mutta moduulilla on yhtä suuri kuin 1. Vektori r - Se on esitetty seuraavasti:

Tästä syystä korvaamalla edellisessä yhtälössä -sellaisella, jolla on r³ Nimittäjässä- lauseke r saavutetaan heti² Nimittäjässä.

Edellä mainittujen vektorien lisäksi kaava sisältää vakiona μ_jompikumpi, puhelu Tyhjiöläpäisevyys ja Kenen arvo on:

μ_jompikumpi = 4π x10^-7 T.m/ a.

Jos haluamme laskea magneettikenttävektorin, on tarpeen integroida kaikki nykyinen jakauma, jota varten tarvitsemme sen geometriaa koskevat tiedot:

Vektorituote ja oikeanpuoleinen sääntö

Biot-Savart-laki sisältää vektorituotteen ID-vektorien välilläs ja r -. Vektorituotteen tulos kahden vektorin välillä on myös vektori.

Tässä tapauksessa ID -vektorituotimoduulis x r - IS: (IDS) ⋅R⋅senθ, missä θ on tunnuksen välinen kulmas ja r -, Kuten kuvassa 1 esitetään.

Tällä tavalla kentän D suuruusB - Se on annettu:

Suunta ja merkitys voidaan määrittää oikean käden sääntöllä, joka on esitetty tässä kuvassa:

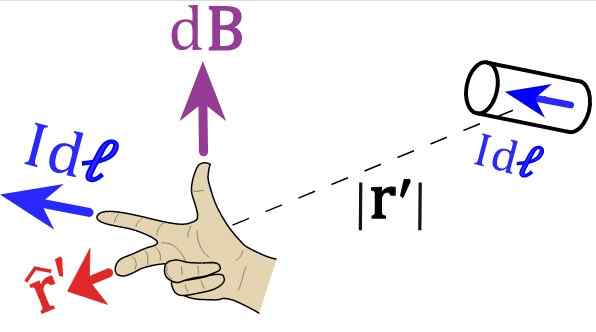Kuva 2. Biot-Savart-lain oikean käden sääntö. Lähde: Wikimedia Commons.

Kutsumme lukijan asettamaan oikean kätensä kuvioiden 1 ja 2 vektorien seurauksena. Kuvalle 1 etusormen on osoitettava vasemmalle tunnuksen jälkeens tai idlens, Keskisormen kohdat vektorin mukaan r - yhtenäinen.

Ja lopulta peukalo on suunnattu ja tämä on magneettikentän suunta.

Voi palvella sinua: ellipsoid: ominaisuudet ja esimerkit

Biot-Savart-lain osoittaminen

Biot-Savart-laki on erittäin kokeellinen, mikä tarkoittaa, että sen formulaatio tulee monista havainnoista nykyisten johtojen tuottaman magneettikentän käyttäytymisestä.

Biot- ja Savart -havainnot

Nämä olivat ranskalaisten tutkijoiden havainnot magneettikentästä DB --

-D: n suuruusB - on käänteisesti verrannollinen r -².

-Se on myös suoraan verrannollinen nykyisen elementin suuruuteen, jota kutsutaan idiksis Ja myös Sen θ: lle, missä θ on vektorien d välinen kulmas ja r -.

-d -dB - on kohtisuorassa molemmille tunnuksilles -virran suunta r -.

-Monipuolinen DB - on radioympyrän tangentiaalinen r - langankestävä. Toisin sanoen nykyisen segmentin tuottama kenttä B koostuu samankeskisistä ympärysmielistä hedelmättömään.

-Merkitys, jossa se pyörii B - Se annetaan oikean peukalon sääntö: oikea peukalo on osoitettu virran suuntaan ja jäljellä olevat neljä sormea ​​käpristyy langan ympärille kentän kiertoaineen jälkeen.

Kaikki nämä havainnot yhdistetään aiemmin kuvatun lain matemaattisessa ilmaisussa.

Biot-Savart Law -hakemukset

Kun nykyisellä jakaumalla on korkea symmetria, integraali voidaan helposti ratkaista, katsotaanpa joitain tapauksia:

Suorasunoinen ja ohut lanka

Strektiliininen lanka, jonka pituus L kuljettaa virran I, kuten kuvassa esiintyvä.

Se kuvaa tarvittavaa geometriaa kentän laskemiseksi. Tämä on kohtisuorassa paperiarkkiin nähden, lähtevä tasolle, jos virta virtaa vasemmalta oikealle ja saapuva muuten (tarkista se oikean käden sääntöllä).

Voi palvella sinua: paramagnetismi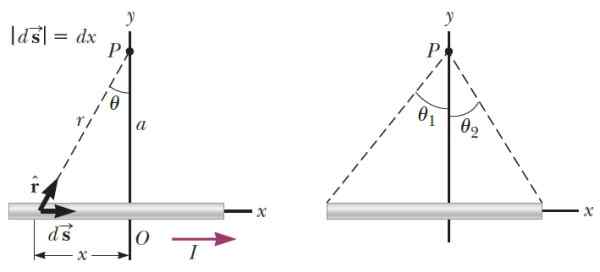Kuva 3.- Vasemmalla puolella geometria, joka on tarpeen magneettikentän laskemiseksi, joka tuottaa ohuen vaijeregmentin pisteessä P. Oikealle kulmat, jotka määrittävät p: n sijainnin suhteessa segmentin päihin. Lähde: Serway, R. Fysiikka tieteen ja tekniikan fysiikka.

Olla k -k -  Yksikkövektori suuntaan kohtisuorassa olevaan suuntaan integroitumisprosessin suorittamisen jälkeen magneettikenttä, jonka lanka tuottaa P: ssä, on:

Pyöreä spira

Radio pyöreä silmukka -lla Se kuljettaa virran kuvan osoittamalla tavalla ja tuottaa magneettikentän DB - -tummanvihreässä- kohdassa P aksiaaliakselilla, etäisyydellä x keskustasta.

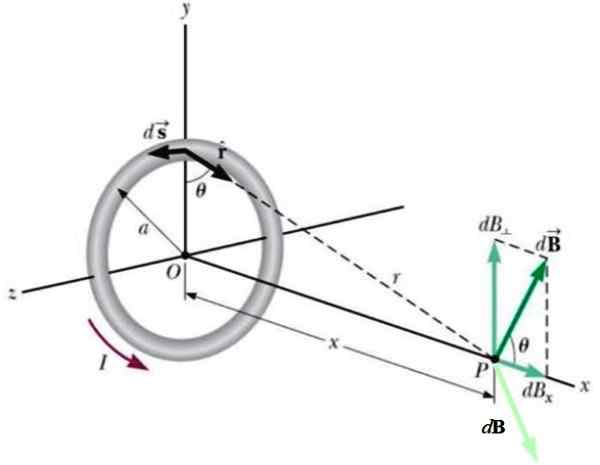Kuva 4.- Geometria ympyräpintaisen spaasin tuottaman kentän laskemiseksi pisteessä P aksiaaliakselilla. Lähde: Wikimedia Commons.

Toinen vastakkaisella puolella sijaitseva virta tuottaa uuden panoksen DB - (vaaleanvihreä), siten, että sen pystysuuntainen komponentti peruutetaan ensimmäisellä.

Tuloksena on, että nettomagneettikenttä on vaakasuora, joten se on integroitu vain näihin komponentteihin, mikä johtaa:

Liikuntaa

On erittäin pitkä lanka, joka kuljettaa 2 virran virtaukseen kuvan osoittamalla tavalla. Laske magneettikentän suuruus 5 cm: n säteittäisellä etäisyydellä langasta.

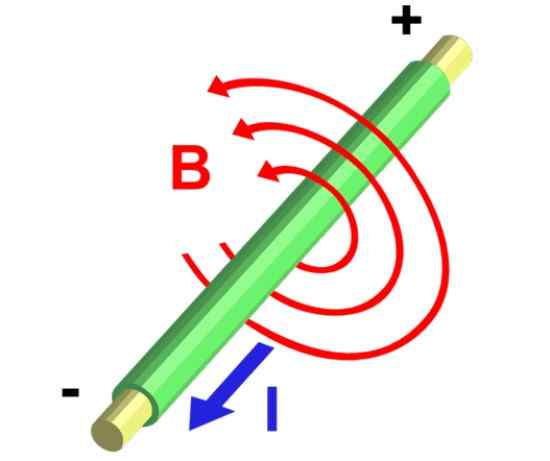Kuva 5.- Virta kuljettaa suoratoistoisen vaijeregmentin magneettikenttälinjat. Lähde: Wikimedia Commons.

Ratkaisu

Koska se on erittäin pitkä lanka, voimme ottaa ilmaisun suoraviivaisen segmentin suhteen ja tehdä θ₁= 0º ja θ₂ = 180º rajakulmissa. Tämä riittää langan pituuteen äärettömyyden säilyttämiseksi.

Tällä tavalla meillä on kenttä:

Se yksinkertaistaa:

Nyt korvaamme lauseen arvot:

I = 2 a

R = 5 x10^-2 m

μ_jompikumpi= 4π x10^-7 T.m/ a

Suunta ja tunne B - Ne on esitetty kuvassa 5, missä arkki jättää suunnan k -k -.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 6. Sähkömagnetismi. Toimittanut Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Resnick, r. 1999. Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
6. Serway, R., Jewett, J. 2008. Fysiikka tieteen ja tekniikan fysiikka. Nide 2. Seitsemäs. Ed. Cengage -oppiminen.