Coulomb Law Selitys, kaava ja yksiköt, harjoitukset, kokeet

Se Coulomb -laki Fyysinen laki säätelee sähköisesti ladattujen esineiden vuorovaikutusta. Ranskalainen tutkija Charles Augustin de Coulomb (1736-1806) totesi sen kokeiden tulosten ansiosta vääntötasapainon kautta.

Vuonna 1785 Coulomb kokenut lukemattomia aikoja pienillä sähköisesti varautuneilla palloilla, esimerkiksi tuomalla tai pois kaksi palloa, muuttaen sen kuorman suuruutta ja myös sen merkkiä. Aina katsomassa ja huolellisesti jokaisen vastauksen rekisteröin.

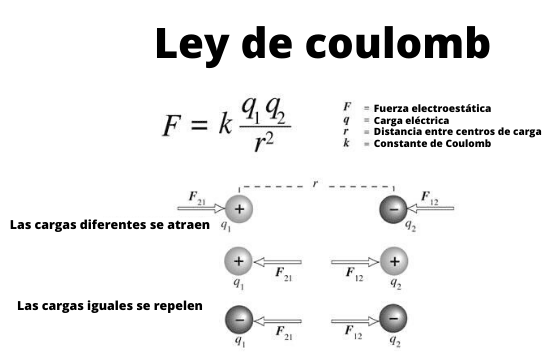
Kuvio 1. Kaavio, joka osoittaa tiettyjen sähkömaksujen vuorovaikutuksen Coulombin lain kautta.

Näitä pieniä palloja voidaan pitää erityiset kuormat, eli esineet, joiden mitat ovat merkityksettömiä. Ja ne täyttyvät, kuten muinaisten kreikkalaisten ajasta lähtien tunnetaan, että saman merkin kuormat hylätään ja erilaisten merkin kuormat houkuttelevat.

Kuva 2. Sotilasinsinööri Charles Coulomb (1736-1806) pidetään Ranskan tärkeimpänä fyysikkona. Lähde: Wikipedia Commons.

Tätä silmällä pitäen Charles Coulomb löysi seuraavan:

-Kahden spesifisen varauksen välinen vetovoima tai torjuminen on suoraan verrannollinen kuormien suuruustuotteeseen.

-Tämä voima on aina suunnattu kuormaan liittyvää linjaa pitkin.

-Lopuksi voiman suuruus on käänteisesti verrannollinen sen etäisyyden neliöön, joka erottaa kuormat.

[TOC]

Coulomb -lain kaava ja yksiköt

Näiden havaintojen ansiosta Coulomb päätteli, että voiman suuruus F Kahden erityismaksun välillä Q -₁ ja Q -₂, erotti etäisyyden r -, Se annetaan matemaattisesti seuraavasti:

Koska voima on vektorien suuruus, sen ilmaisemiseksi yksikkövektori on täysin määritelty r - Kuormitukseen liittyvän linjan suuntaan (yksikkövektorin suuruus on yhtä suuri kuin 1).

Lisäksi edellisen lausekkeen välttämätöntä suhteellisuusvakion tasa -arvoksi kutsutaan k_ja tai yksinkertaisesti k: sähköstaattinen vakio jompikumpi Coulomb vakiona.

Lopuksi perustetaan Coulombin täsmällisiä kuormituksia koskeva laki: Annetaan:

Voima, kuten aina kansainvälisessä yksikköjärjestelmässä, tulee Newton (N). Maksujen osalta yksikköä kutsutaan coulombiksi (c) Charles Coulombin kunniaksi ja lopulta etäisyys r tulee metreinä (M).

Tarkkailemalla tarkkaan edellistä yhtälöä, on selvää, että sähköstaattisella vakiona on oltava n: n yksiköt.m² / C², Newtonsin saamiseksi seurauksena. Vakion arvo määritettiin kokeellisesti seuraavasti:

Voi palvella sinua: Vapaat vektorit: Ominaisuudet, esimerkit, harjoitukset

k -k -_ja = 8.89 x 10 ⁹ N.m² / C² ≈ 9 x 10 ⁹ N.m² / C²

Kuvio 1 kuvaa kahden sähköisen varauksen välistä vuorovaikutusta: kun ne ovat sama merkki, ne ovat hylättyjä, muuten ne houkuttelevat.

Huomaa, että Coulombin laki sopii Newtonin kolmanteen lakiin tai toiminta- ja reaktioihin, siten suuruudet F₁ ja F₂ Ne ovat samoja, osoite on sama, mutta aistit ovat vastakkaisia.

Kuinka soveltaa Coulombin lakia

Sähkömaksujen välisten vuorovaikutusten ratkaisemiseksi seuraava on otettava huomioon:

- Yhtälöä käytetään yksinomaan tiettyjen kuormitusten, ts. Jos ladatuilla objekteilla on mitattavissa olevat mitat, on tarpeen jakaa ne hyvin pieniin kuormiin ja lisätä sitten kunkin kuorman vaikutukset, joille vaaditaan kattava laskelma.

- Sähkövoima on vektorin suuruus. Jos vuorovaikutusta on enemmän kuin kaksi, kuorman q nettovoima_Yllyttää Se annetaan superpositioperiaatteella:

F_Netto = F_I1 + F_I2 + F_i3 + F_i4 +… = ∑ F_ij

Missä alaindeksi J - Vale 1, 2, 3, 4 ... ja edustaa kutakin jäljellä olevaa kuormaa.

- Sen on aina oltava yhdenmukainen yksiköiden kanssa. Yleisin on työskenteleminen sähköstaattisen vakion kanssa yksiköissä, jos sinun on varmistettava, että kuormat ovat Coulombissa ja etäisyydet metreinä.

- Lopuksi yhtälöä käytetään, kun kuormat ovat staattisessa saldossa.

Ratkaisut

- Harjoitus 1

Seuraavassa kuvassa on kaksi erityistä kuormaa +Q ja +2Q. Kolmas täsmällinen kuorma --q asetetaan p: lle. Tätä kuormaa pyydetään löytämään sähkövoima muiden läsnäolon vuoksi.

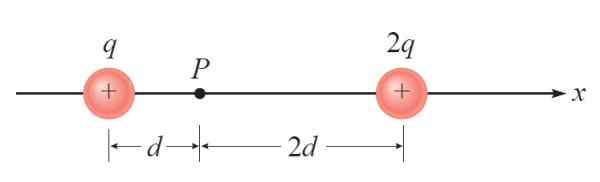Kuva 3. Vuoden kaavio ratkaistu 1. Lähde: Giambattista, a. Fysiikka.

Ratkaisu

Ensimmäinen asia on perustaa sopiva referenssijärjestelmä, joka tässä tapauksessa on vaakasuora akseli tai x -akseli. Tämän järjestelmän alkuperä voi olla missä tahansa, mutta mukavuudella se sijoitetaan P: hen, kuten kuvassa 4a esitetään:

Voi palvella sinua: Bethelgeuse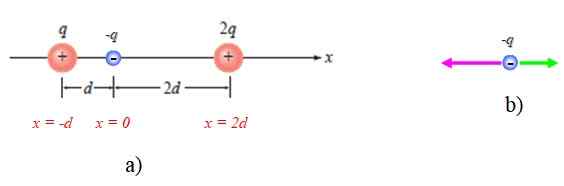Kuva 4. Vuoden järjestelmä ratkaistu 1. Lähde: Giambattista, a. Fysiikka.

Näytetään myös joukkojen kaavio, kun otetaan huomioon, että se houkuttelee kahta muuta (kuva 4b).

Soitetaan F₁ Voimaan, joka käyttää kuormaa, joka kuormituksessa -Q: lla ne on suunnattu X -akselia pitkin ja negatiivisen merkityksen pisteet, siksi:

Yksikkövektori x -akselin suuntaan on x Ympyrä -aksentti yhtälössä. Tämä on yleinen merkintä yksikkövektorille. Vähemmän merkkiä ilmestyy, koska voima F₁ pisteitä akselin negatiivisessa merkityksessä.

Analoginen lasketaan F₂-

Huomaa, että F₂ Se on puolet F₁, Vaikka kuorma on kaksinkertainen. Nettovoiman löytämiseksi ne lisätään vihdoin vektorisesti F₁ ja F₂-

F_Netto = (-K + K/2).(Q² /D²) (x) N = - (k/2).(Q² /D²) (x) N

- Harjoitus 2

Kaksi polystyreenipalloa, joilla on yhtä suuri massa m = 9.0 x 10^-8 KG: llä on sama positiivinen kuorma Q ja suspendoituu silkkikierällä pituus L = 0,98 m. Pallot erotetaan d = 2 cm: n etäisyys. Laske.

Ratkaisu

Lausunnon tilanne on kuvattu kuvassa 5a.

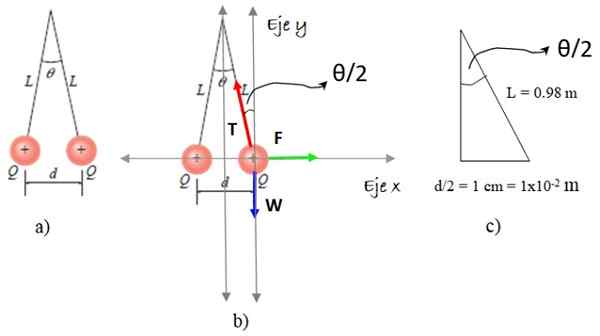Kuva 5. Harjoituksen 2 ratkaisemiseksi järjestelmät. Lähde: Giambattista, a. Fysiikka /f. Zapata.

Valitsimme yhden pallot ja siihen piirrämme eristetyn kehon kaavion, joka sisältää kolme voimaa: paino: W -, Köyden jännitys T ja sähköstaattinen torjuminen F, kuten kuvassa 5b näkyy. Ja nyt vaiheet:

Vaihe 1

Θ/2: n arvo lasketaan kuvan 5C kolmiolla:

θ/2 = Arcsen (1 x 10^-2/0.98) = 0.585º

Vaihe 2

Sitten sinun on sovellettava Newtonin toista lakia ja otettava 0, koska maksut ovat staattisessa saldossa. On tärkeää korostaa tätä jännitystä T Se on kalteva ja siinä on kaksi komponenttia:

∑f_x = -T.sin θ + f = 0

∑f_ja = T.cos θ - w = 0

Vaihe 3

Poistamme viimeisen yhtälön jännityksen suuruuden:

Se voi palvella sinua: Dynamiikka: Historia, mitä tutkimuksia, lakeja ja teorioita

T = w/ cos θ = mg/ cos θ

Vaihe 4

Tämä arvo korvataan ensimmäisessä yhtälössä F: n suuruuden löytämiseksi:

F = t sin θ = mg (sin θ / cos θ) = mg. Tg θ

Vaihe 5

Kuten f = k q² /D², Se tyhjentää K:

Korvaamalla lauseen tarjoamat numeeriset arvot, se saadaan:

Q = 2 × 10^-yksitoista C.

Kokeet

Coulombin lain tarkistaminen on yksinkertaista vääntötasapainon avulla, joka on samanlainen kuin hänen laboratoriossaan käytetty.

On kaksi pientä Saúcon palloa, joista yksi, yhden tasapainon keskellä, ripustetaan langasta. Koe koostuu koskettaa Saúco -palloja, jotka on ladattu toisella metallipalloilla, jotka on ladattu kuormalla q.

Kuva 6. Coulombin vääntötasapaino.

Välittömästi kuorma jakautuu tasaisesti kahden Saúco -pallon välillä, mutta sitten, samoin kuin saman merkin kuormat, ne hylkäävät. Voima, joka aiheuttaa langan vääntö langasta ja siirtyy välittömästi pois kiinteästä palloista, toimii keskeytettyyn palloon.

Sitten näemme, että se vaihtelee muutaman kerran, kunnes tasapaino saavuttaa. Sitten sitä pitävän palkin tai langan vääntö tasapainottaa sähköstaattinen torjuntavoima.

Jos pallot olivat alun perin 0, nyt matkapuhelin on kääntynyt kulmaan θ. Tasapainon ympärillä on tutkinnon suorittanut nauha asteina tämän kulman mittaamiseksi. Kun aiemmin määritetään vääntövakio, niin Saúco -pallojen hankkiman kuorman arvon ja arvon arvon ja arvon arvo on helposti laskettu.

Viitteet

1. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Sähköstaatiikka. Toimittanut Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysiikka. Toinen painos. McGraw Hill.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Resnick, r. 1999. Fyysinen. Osa. 2. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Nide 2.