Faradayn kaavalaki, yksiköt, kokeet, liikunta,

Se Faradayn laki Sähkömagnetismissa se osoittaa, että muuttuva magneettikentän virtaus pystyy indusoimaan sähkövirta suljetussa piirissä.

Vuonna 1831 englantilainen fyysikko Michael Faraday kokenut liikkuvia kuljettajia magneettikentän sisällä ja myös vaihtelevat magneettikentät, jotka ylittivät kiinteät ohjaimet.

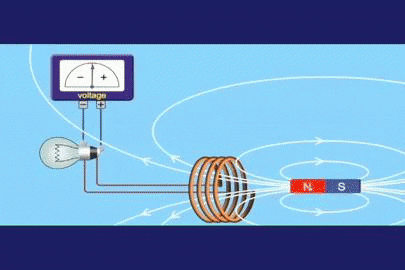Kuvio 1. Faradayn induktiokoe

Faraday tajusi, että jos hän vaihtelee magneettikentän virtausta ajoissa, hän pystyi luomaan jännitteen verrannollisesti mainittuun variaatioon. Jos ε on indusoitu elektromotorinen jännite tai voima (indusoitu FEM) ja φ on magneettikentän virtaus, matemaattisessa muodossa se voidaan ilmaista:

| ε | = Δφ/ΔT

Missä symboli δ osoittaa määrän vaihtelun ja FEM: n palkit osoittavat tämän absoluuttisen arvon. Koska se on suljettu piiri, virta voi kiertää yhteen tai toiseen.

Magneettinen flux, jonka magneettikentällä on pinnan läpi, voi vaihdella eri tavoin, esimerkiksi:

-Bar -magneetin siirtäminen pyöreän spiraalin läpi.

-Silmukan ylittävän magneettikentän voimakkuuden lisääminen tai vähentäminen.

-Pellon jättäminen korjattu, mutta jollakin mekanismilla muuttaa silmukan aluetta.

-Yllä olevien menetelmien yhdistäminen.

Kuva 2. Englantilainen fyysikko Michael Faraday (1791-1867).

[TOC]

Kaavat ja yksiköt

Oletetaan B -.

Magneettikentän virtaus φ on skalaarinen määrä, joka viittaa alueen a ylittävien kenttälinjojen määrään. Kuviossa 1 ovat valkoiset viivat, jotka jättävät magneetin pohjoisnavan ja palaavat etelään.

Voi palvella sinua: Brayton Cycle: Prosessi, tehokkuus, sovellukset, harjoitukset

Pellon voimakkuus on verrannollinen linjojen lukumäärään alueyksikköä kohti, joten voimme nähdä, että pylväissä se on erittäin voimakas. Mutta meillä voi olla erittäin intensiivinen kenttä, joka ei tuota virtausta silmukassa, jonka voimme saavuttaa muuttamalla tämän (tai magneetin) suuntausta.

Suuntakerroin huomioon ottamiseksi magneettikentän virtaus määritellään skalaarituotteeksi B - ja n, olemus n Normaali yksikkövektori spaasin pintaan ja se osoittaa sen suuntauksen:

Φ = B -Ollan A = BA.cosθ

Missä θ on kulma B - ja n. Jos esimerkiksi B - ja n Ne ovat kohtisuorassa, magneettikentän virtaus on tyhjä, koska siinä tapauksessa kenttä on tangentti spaasitasolle eikä voi ylittää sen pintaa.

Sen sijaan B - ja n Ne ovat yhdensuuntaisia, se tarkoittaa, että kenttä on kohtisuorassa Spira -tasoon nähden ja viivat kulkevat sen läpi maksimiin.

F: n kansainvälinen järjestelmäyksikkö on Weber (W), missä 1 W = 1 T.m² (lukee "Tesla neliömetriä kohti").

Lenzin laki 

Kuviossa 1 voidaan nähdä, että jännitteen napaisuus muuttuu magneetin liikkuessa. Polaarisuus vahvistetaan Lenzin lailla, jonka mukaan indusoidun jännitteen on vastustettava sitä tuottavaa variaatiota.

Jos esimerkiksi magneetin tuottama magneettinen vuoto kasvaa, kuljettaja vahvistaa virran, joka kiertää luomalla oman virtauksensa, joka vastustaa tätä kasvua.

Jos päinvastoin, magneetin aiheuttama virtaus vähenee, indusoitu virta kiertää siten, että sen oma virtaus torjuu mainitun laskun.

Voi palvella sinua: lämpömittakaavat

Tämän ilmiön huomioon ottamiseksi Faradayn lakiin asetetaan negatiivinen merkki, eikä absoluuttisten arvopalkkien asettaminen enää välttämätöntä:

ε = -δφ/ΔT

Tämä on Faraday-Lenzin laki. Jos virtauksen vaihtelu on äärettömää, deltat korvataan eroilla:

ε = -dφ/dt

Aikaisempi yhtälö on voimassa silmukassa. Mutta jos meillä on kehruu kela, tulos on paljon parempi, koska FEM kertoo N kertaa:

ε = - n (dφ/dt)

Faraday -kokeet

Virran tuottamiseksi, joka valaisee hehkulampun, magneetin ja spiraalin välillä on oltava suhteellinen liike. Tämä on yksi tapa, jolla virtaus voi vaihdella, koska tällä tavalla silmukan ylittävän kentän voimakkuus muuttuu.

Tällä hetkellä magneettiliike lakkaa, polttimo sammuu, vaikka magneetti jätetään edelleen spaasiin. Virran kiertämiseen lamppuun tarvitaan, että kenttävirta vaihtelee.

Kun magneettikenttä vaihtelee ajan myötä, voimme ilmaista sen seuraavasti:

B - = B - (T).

Pidä spaasin alue vakiona ja jättämällä se kiinnitettynä vakiokulmaan, joka kuvan tapauksessa on 0º, sitten:

 Kuvion 1 (cos 0º = 1) silmukka:

Muuttuva pinta -ala

Jos pystyt vaihtamaan spaase -aluetta jättäen sen suunnan kiinnittämisen ja asettamalla sen vakion kentän keskelle, indusoitu fem annetaan:

Yksi tapa saavuttaa tämä on laittaa palkki, joka liukuu johtavalle kiskolle tietyllä nopeudella, kuten seuraavassa kuvassa esitetään.

Voi palvella sinua: ío (satelliitti) Kuva 3. Liukutuottaja. Lähde: Serway, R. Fysiikka tieteen ja tekniikan fysiikka.

Pylväs ja kisko sekä lamppu tai kuljettajajohdolla kytketty vastus muodostavat suljetun piirin suorakaiteen muotoisen spaasin muodossa.

Kun liu'uta palkkia, pituus x Kasvu tai vähenee, ja sen mukana silmukan pinta -ala muuttuu, mikä riittää muuttuvan virtauksen luomiseen.

Magneettisen vuon vaihtelu kiertolla

Kuten aiemmin sanoimme, jos kulma B - Ja silmukan normaali on vaihdettu, kenttävirta muuttuu seuraajan mukaan:

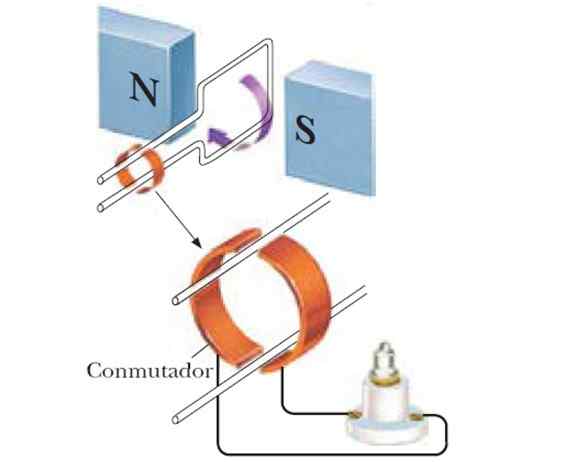Kuva 4. Jos silmukka kierretään magneetin napojen keskuudessa, saadaan sinimuotoinen generaattori. Lähde: f. Zapata.

Sinusoidinen generaattori saadaan siten, ja jos käytetään yhtä määrää keloja, indusoitu FEM on suurempi:

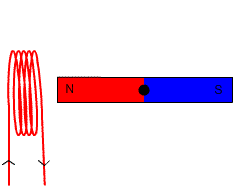Kuva 5. Tässä generaattorissa magneettia pyöritetään kelan virran indusoimiseksi. Lähde: Wikimedia Commons.

Liikuntaa

Pyöreä käämi n kierroksista ja radiosta r kääntyy kulmallisesti ω magneettikentän keskelle B -arvon B. Löydä lauseke kelaan maksimalle indusoidulle FEM: lle.

Ratkaisu

Kiertoa aiheuttamaa fem -lauseketta käytetään, kun kela on n kierroksia, tietäen, että:

-Kela -alue on a = πr²

-Kulma θ vaihtelee riippuen ajasta θ = ωt

On tärkeää ottaa huomioon, että θ = ωt korvataan ensin Faradayn laissa ja sitten Se on johdettu ajasta:

ε = -nba (cos θ) '= -nb (πr²-A.[cos (ωt)] '= nbω (πr²) Sen (ωt)

Koska enimmäis FEM: tä pyydetään, tämä tapahtuu aina kun sen ωt = 1, niin lopulta:

ε_max = NBω (πr²-A

Viitteet

1. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Osa 6. Sähkömagnetismi. Toimittanut Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysiikka. Toinen painos. McGraw Hill.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed. Prentice Hall.
4. Resnick, r. 1999. Fyysinen. Osa. 2. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Nide 2.