Hooke Law -kaavat, esimerkit, hakemukset, harjoitukset

Se Hooken laki huomauttaa, että elastisen esineen kokemat muodonmuutokset ovat suoraan verrannollinen siihen kohdistuvaan voimaan. Suhteellisuusvakio riippuu esineen luonteesta, sen geometriasta ja materiaalista, jolla se on valmistettu.

Kaikilla materiaaleilla on joustavia ominaisuuksia suuremmassa tai pienemmässä määrin, joten ne noudattavat Hooken lakia aina kun ne palaavat alkuperäisiin mittoihinsa, kun voima lakkaa. Joustavat jouset ja ikenet ovat hyviä esimerkkejä esineistä, jotka noudattavat Hooken lakia, mutta samoin teräs cabillas, jotka ovat osa siltaa.

Kuvio 1. Hooken laki keväällä

Esimerkiksi jousen tai telakan pitämiseksi sen venytettynä tai pakattuna on välttämätöntä käyttää voima, jonka suuruus on f. Hooken lain mukaan kevät kokee X -muodonmuutoksen:

F ∝ x

Suhteellisuusvakio, jota kutsutaan kevääksi jousen jäykkyys, Siksi se on nimellä k,:

F = k⋅x

Kansainvälisen järjestelmän yksiköissä voima tulee Newton (N) ja muodonmuutokset metreinä (M). Siksi kevään vakiossa on N/M -yksiköt. Keväänvakio edustaa voimaa, jota on käytettävä sen muodonmuutokseen 1 m pituudeltaan.

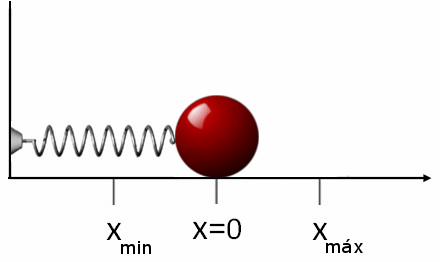Kuva 2. Kun jousi venytetään, esineeseen kohdistettu voima on päinvastoin. Sama tapahtuu, jos jousi kutistuu, tässä tapauksessa se ajaa esinettä päinvastaisessa merkityksessä. Lähde: Wikimedia Commons.

Jos jousen venyttämisen tai puristamisen jälkeen se vapautetaan, se liikkuu vastakkaiseen suuntaan kuin käytetty voima. Tämä tarkoittaa, että jos venytämme sitä, se on pakattu ja päinvastoin. Siksi Force F_{R -} että Kevätharjoitukset On:

F_{R -} = -k⋅x

Negatiivinen merkki osoittaa, mitä sanotaan: että voima vastustaa siirtymistä, joten tämä voima tunnetaan nimellä Palauttava voima.

[TOC]

Kaava ja yhtälöt

Robert Hooke (1635-1703) löysi voiman ja siirtymän välisen suhteen keväällä, huomattava englantilainen fyysikko ja joka tunnetaan kilpailustaan ​​Isaac Newtonin kanssa. Hooke oli monipuolinen tutkija, joka menestyi menestyksekkäästi tieteen eri aloilla: mekaniikka, biologia, tähtitiede ja arkkitehtuuri.

Kuva 3. Englantilainen fyysikko Robert Hooke, joka ei tunne aikan muotokuvia. Tämä on taiteilija Rita Gererin vuonna 2004 tekemä jälleenrakennus kuvauksien avulla, jotka tapasivat tutkijan tavanneet. Lähde: Wikimedia Commons. Rita Greer / Fal.

Hooke tajusi, että jos laituriin kohdistuva voima ei ole kovin suuri, laituri on suhteellisesti muodonmuutos pakottamiseksi, ja kun sanottu voima katoaa, jousella on jälleen luonnollinen pituus.

Voi palvella sinua: Maan magnetosfääri: Ominaisuudet, rakenne, kaasut

Tällä tavoin Hooken laki graafisesti on suoran linjan muoto, jonka kaltevuus on jousivakio. Seuraava kuva näyttää jouselle kohdistetun voiman venyttääksesi sitä - tai puristaa sitä - X -asennosta riippuen. Huomaa, että voima ei riipu jousen luonnollisesta pituudesta, vaan sen siirtymisestä.

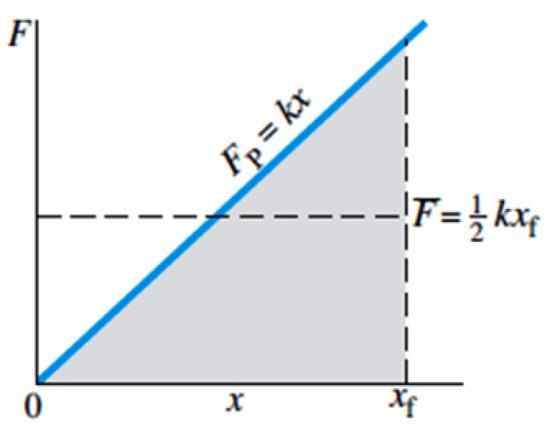Kuva 4. Tarvittavan voiman suuruus F jousi venyttämiseen tai puristamiseen X -muodonmuutoksesta riippuen. Lähde: Giancoli, D. Fysiikka sovelluksilla.

Keskimääräinen voima on osoitettu kaaviossa F baarilla ja vastaa ½ kx_F, missä x_F on kevään viimeinen sijainti.

Sekä keväällä kohdistuva voima että hänelle sidottu esineeseen kohdistuva voima ovat muuttuvia voimia. Mitä enemmän haluat venyttää tai puristaa kevään, sitä enemmän voimaa sinun on käytettävä saavuttamaan sen.

Työ tehdään jousen venyttämiseksi tai puristamiseksi

Kun sovelletaan voimaa, joka muodostaa jousen, keväällä tallennettu työ tehdään ja sitä voidaan käyttää myöhemmin.

Mekaaninen työ määritellään alueeksi F voimakaavion alla sijainnista x riippuen. Laskea työ w, jonka muuttuva voima F (x) tekee objektia siirtäessäsi asennosta x₁ sijoittaa x₂ Määritelty integraali on laskettava:

Työn tapauksessa, joka tarvitaan jousen saattamiseksi tasapainoasennosta asentoon x_F Se on hyvin yksinkertainen, koska laskettava alue on kuvan 4 harmaan varjostetun kolmion alue, jonka kaava on tiedossa:

Kolmion alue = ½ pohja. korkeus

Siksi tarvittava työ on:

W = ½ x_F . (KX_F) = ½ k (x_F-A²

Ja jos haluat laskea tarvittavan työn, jotta saadaan kevää asennosta x asentoon x_F, Se vastaa kuvassa 5 naarmuuntuneen trapetsin alueen laskemista:

W = ½ k (x_F-A² - ½ k x²

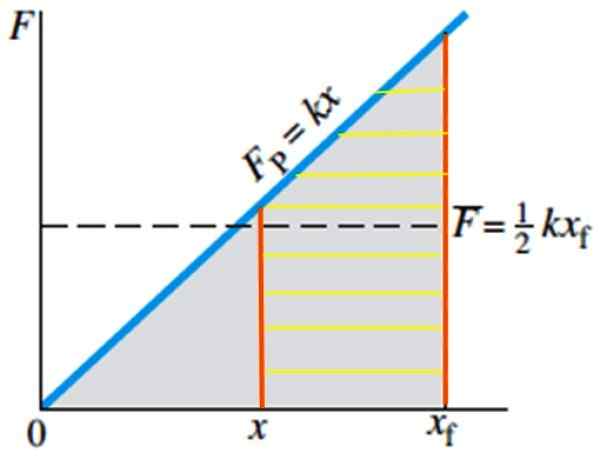Kuva 5. Työt, jotka tehdään jousen venyttämiseksi asemasta X XF -asentoon, joka vastaa Rayadan aluetta. Lähde: Giancoli, D. Fysiikka sovelluksilla.

Esimerkkejä lähteistä

Niiden sovelluksen mukaan jouset voivat olla lieriömäisiä, kartiomaisia, kierteitä, pyöreällä poikkileikkauksella (yleisin), neliö- tai suorakulmainen osa.

Voi palvella sinua: sähköjohtimet

Laajasti käytetty luokittelu on sen tyypin mukaan, johon ne altistetaan: on vääntö, taivutus, puristus- ja laajennusjouset. Jälkimmäisiä käytetään laajasti ja työskentelee myös jännityksen ja puristuksen kannalta.

Puristusjousi

Esimerkki pakkausjousesta on se, mitä käytetään nimeltään lelussa Pogo jompikumpi Saltoín Palo. Nämä jouset säilyttävät melko potentiaalisen energian pakattuna ja vapautuessaan asteittain palaamalla tasapainoasentoon. Tällä tavoin palautukset eivät ole liian äkillisiä.

Kuva 6. Pogo tai Saltoín -tikku perustuu puristusjouseen. Lähde: Wikimedia Commons.

Laajennus- ja vääntöjouset

Sprampien jousi on jatkojousien tyyppi ja ne on valmistettu hyvin ryömitetyillä käännöksillä, kaksi koukkua päissä. He kykenevät säilyttämään tarpeeksi potentiaalienergiaa, jonka he myöhemmin vapautuvat, kun joku nousee ja alkaa hypätä kankaalle, jolla on myös oma joustava vaste, kuten kaikki materiaalit.

Vääntöjouset ovat hyvin yleisiä, koska ne palvelevat vaatteiden kiinnittimiä. Päällisten koukkujen sijasta ne taipuvat kulmassa vastustamaan voimia, joilla on taipumus käyttää vääntöä.

Kuva 7. Jouset ovat osa lukemattomia mekanismeja, kuten nämä vaatteet pinsetit. Lähde: PxFuel.

Materiaalit valmistusjousille

Sopivimpia materiaaleja jousien valmistukseen ovat ne, joilla on a Lopullinen vastustuskyky (Lopullinen vastus), ts. He tukevat suurta vaivaa ennen rikkoutumista. On myös kätevää, että materiaalilla on korkea rypistymispiste, joten se ei menetä joustavia ominaisuuksiaan pienillä ponnisteluilla.

Teollisuuden käyttöjouset valmistetaan seoksilla, jotka sisältävät terästä, jossa on korkea hiili-, kupari-, nikkeli- ja pronssipitoisuus.

Hooken lakahakemukset

Koska jousilla on potentiaalienergian säilyttämistä venyessään tai puristuessaan, he kykenevät tekemään työtä siirtämällä esimerkiksi mekanismeja.

Tällä tavoin jousilla on monia sovelluksia pienistä ja päivittäisistä esineistä, autojen kautta, kaikenlaisiin koneisiin. Jouset palvelevat:

-Iskuvärähtely.

-Valmistaminen sisäänvedettävät mekanismit: kynä, roikkuvat pinsettit, hiuskoukut.

-Tehdä kevät- tai dynamometrit

Ja ne ovat myös osa:

Voi palvella sinua: suljettu sähköpiiri

-Kellot.

-Trampoliinit.

-Lukot.

-Lelut.

-Aseet.

-Neulamittarit, esimerkiksi galvanometri, jota käytetään virtojen, jännitteiden ja vastusten mittaamiseen.

Ratkaisut

- Harjoitus 1

Voimakkuus 5 kohdistetaan.0 n keväällä, mikä on 3 venytystä.5 cm sen luonnollisesta pituudesta.

a) kuinka paljon venytetään, kun sovellettu voima on 7 n?

b) Löydä kohdistetun voiman tekemä työ venyttääksesi jouseen 3.5 cm sen luonnollisesta pituudesta.

Liittää jhk

Tietäen, että jousi on venytys 3.5 cm 5: n avulla 5.0 N Voimme laskea vakioasi:

k = f / x = 5.0 N / 3.5 cm = 1.43 N / cm.

Kun 7 N: n voima kohdistetaan, saadaan seuraava venytys:

x = f / k = 7.0 N / 1.43 N/M = 4.9 cm

Ratkaisu b

Tarvittava työ jousen muodonmuutokselle annetaan:

W = ½ kx² = 0.5 x 1.43 N / cm x (3.5 cm)² = 8.76 n . CM = 8.76 n . 1 x10 ^-2 M = 0.0876 J.

- Harjoitus 2

Kevää halveksittavaa taikinaa ja 10 cm pitkä roikkuu tuesta. Jos ripustetaan 2 kg: n massa, jousi on venytetty, kunnes se saavuttaa 15 cm. Laskea:

a) jousivakio

b) jousikoko, kun 3 kg: n massa on ripustettu.

Liittää jhk

Jousen venytys on x = 15 - 10 cm = 5 cm

Koska järjestelmä on staattisessa tasapainossa, jousen aiheuttama voima, kun venytys on suunnattu pystysuoraan ylöspäin, painon kompensoimiseksi, joka on suunnattu alas, sitten:

F_{R -} = W → kx = mg

K = 2 x 9.8 N / 5 x10 ^-2 M = 392 N/M

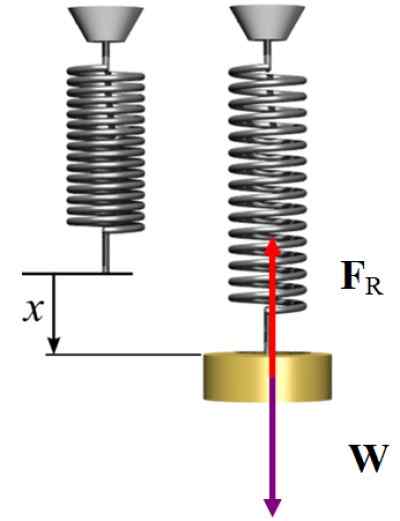Vapaa kehon kaavio liikunnasta ratkaistu 2. Lähde: Wikimedia Commons/F. Zapata.

Ratkaisu b

Kun 3 kg paino on suspendoitu, uusi voima on w = 3 x 9.8 n = 29.4 n

Tässä tapauksessa venytys on:

x = mg /k = 29. 4 N / 392 N / M = 0.075 m = 7.5 cm

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Luovat mekanismit blogi. Neljä erityyppistä jousia. Toipunut: creativeMechanismit.com.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 2. Dynaaminen. Toimittanut Douglas Figueroa (USB).
4. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed. Prentice Hall.
5. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa.  Pearson.