Sandwich Law Selitys ja harjoitukset

Se Voileipälaki tai tortilla on menetelmä, jonka avulla voidaan toimia fraktioilla; Erityisesti sen avulla voit jakaa fraktioita. Toisin sanoen tämän lain kautta voit tehdä rationaalisia lukuja jakoja. Sandwichin laki on hyödyllinen ja yksinkertainen työkalu muistaa.

Tätä artikkelia pidetään vain rationaalisten lukujen jakautumisen tapauksessa, jotka eivät ole molemmat kokonaisia ​​lukuja. Nämä rationaaliset luvut tunnetaan myös murto- tai rikkoutuneina lukuina.

Selitys

Oletetaan. Sandwich -laki koostuu tämän jaon ilmaisemisesta seuraavasti:

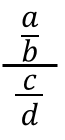
Tämä laki osoittaa, että tulos saadaan kertomalla yläpäässä sijaitseva luku (tässä tapauksessa luku "A") alaosan lukumäärällä (tässä tapauksessa "D") ja jakamalla tämä kertolasku tuotteen välillä Keskimääräiset numerot (tässä tapauksessa "B" ja "C"). Siten edellinen jako on yhtä suuri kuin × D/B × C.

Se voidaan havaita ilmaista edellistä jakautumista, että keskiviiva on pidempi kuin murto -luvut. On myös arvostettu, että se on samanlainen kuin voileipä, koska tapas ovat murto -lukuja, jotka haluat jakaa.

Tätä jakotekniikkaa tunnetaan myös nimellä kaksois C, koska suurta “C” voidaan käyttää äärimmäisten lukujen ja pienemmän “C” tunnistamiseen keskipitkien numeroiden tuotteen tunnistamiseksi:

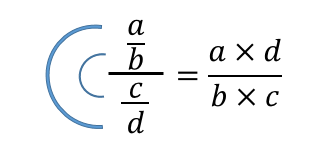
Kuva

Murto- tai rationaaliset numerot ovat m/n -muodon lukuja, joissa "m" ja "n" ovat kokonaisia ​​lukuja. Rationaalisen luvun m/n kerrottava käänteinen käännös koostuu toisesta rationaalisesta lukumäärästä, joka kertomalla se M/N: llä johtaa numeroon yksi (1).

Tätä moninkertaista käänteistä merkitään (m/n)^-1 Ja se on yhtä suuri kuin n/m, koska m/n × n/m = m × n/n × m = 1. Merkityksellä sinun on myös (m/n)^-1= 1/(m/n).

Sandwich -lain matemaattinen perustelu, samoin kuin muut olemassa olevat tekniikat jakamaan fraktioita, on siinä, että jakamalla kaksi rationaalista numeroa A/B ja C/D, taustalla, mitä tehdään, on A/B: n kertolasku c/d. Tämä on:

A/b ÷ c/d = a/b × 1/(c/d) = a/b × (c/d)^-1= A/B × D/C = A × D/B × C, kuten aiemmin on saatu.

Jotta ei voida työskennellä enemmän, jotain, joka on otettava huomioon ennen voileivän lain käyttämistä, on, että molemmat fraktiot ovat mahdollisimman yksinkertaistettuja, koska on tapauksia, joissa ei ole tarpeen käyttää lakia.

Esimerkiksi 8/2 ÷ 16/4 = 4 ÷ 4 = 1. Voilein lakia olisi voitu käyttää, saada sama tulos yksinkertaistamisen jälkeen.

Toinen tärkeä asia, joka on otettava huomioon, on, että tätä lakia voidaan käyttää myös, kun kokonaisluku vaatii murto -lukumäärää. Tässä tapauksessa 1 on sijoitettava kokonaisluvun alle ja jatkettava voileivän lakia kuten aiemmin. Tämä johtuu siitä, että mikä tahansa kokonaisluku K täyttää sen k = k/1.

Harjoitukset

Alla on sarja jako, jossa voileivän lakia käytetään:

• 2 ÷ (7/3) = (2/1) ÷ (7/3) = (2 × 3)/(1 × 7) = 6/7.
• 2/4 ÷ 5/6 = 1/2 ÷ 5/6 = 1 × 6/2 × 5 = 6/10 = 3/5.

Tässä tapauksessa fraktiot 2/4 ja 6/10 yksinkertaistettiin jakamalla 2 ylös ja alas. Tämä on klassinen menetelmä, jolla yksinkertaistetaan fraktioita, jotka koostuvat osoittajan yhteisten jakajien löytämisestä ja nimittäjästä (jos sellaista) että sekä yhteisen jakajan välillä, kunnes saadaan irrontamaton fraktio (jossa ei ole yhteisiä jakajia).

• (xy+y)/z ÷ (x+1)/z²= (xy+y) z²/z (x+1) = (x+1) yz²/z (x+1) = yz.

Viitteet

1. Almaguer, G. (2002). Matematiikka 1. Toimituslimusa.
2. Álvarez, J., Jácome, J., López, J., Cruz, E. d -d., & Tetumo, J. (2007). Matematiikka, tukielementit. Yksinäinen. J -. Tabascon autonominen.
3. Takuita, b. (1839). Aritmeettisen periaatteet. Painanut Ignacio Täytetty.
4. Barker, l. (2011). Matematiikan tasoitetut tekstit: numero ja toiminnot. Opettajan luomat materiaalit.
5. Barrios, a. -Lla. (2001). Matematiikka 2nd. Toimitusohjelma.
6. Eguiluz, m. Lens. (2000). Fraktiot: päänsärky? Uudet kirjat.