Estä algebraelementit, esimerkit, harjoitukset ratkaistu

Hän Lohkoalgebra Se viittaa joukkoon, jotka suoritetaan lohkojen kautta. Nämä ja jotkut muut elementit edustavat kaavamaisesti järjestelmää ja visualisoimaan helposti vastauksesi tiettyyn merkintöön.

Yleensä järjestelmä sisältää erilaisia ​​sähköisiä, elektronisia ja sähkömekaanisia elementtejä, ja jokainen niistä, niiden toiminnassa ja asennossa järjestelmässä, samoin kuin tapa, jolla ne liittyvät toisiinsa.

Kuvio 1.

Yllä olevassa kuvassa on hyvin yksinkertainen järjestelmä, joka koostuu tulosignaalista X (S), joka siirtyy lohkoon siirtofunktiolla G (S), joka muuttaa sitä ja tuottaa tulosteen y (s).

On kätevää edustaa signaaleja ja heidän matkaa järjestelmän läpi nuolien kautta, jotka tulevat ja jättävät jokaisen lohkon. Yleensä signaalin virtaus on suunnattu vasemmalta oikealle.

Tällaisen järjestelmän etuna on visuaalinen apu, jonka se tarjoaa järjestelmän ymmärtämiselle, vaikka se ei ole sama fyysinen esitys. Itse asiassa lohkokaavio ei ole ainutlaatuinen, koska näkökulman mukaan jopa useita saman järjestelmän kaavioita voidaan piirtää.

Voi myös tapahtua, että samaa kaaviota käytetään useisiin järjestelmiin, jotka eivät välttämättä liity toisiinsa, mikäli sen käyttäytyminen kuvaa oikein. On olemassa erilaisia ​​järjestelmiä, joiden vaste on samanlainen monissa näkökohdissa, esimerkiksi LC-piiri (induktorikanava) ja massaresortin järjestelmä.

[TOC]

Mikä on lohkokaavio?

Järjestelmät ovat yleensä monimutkaisempia kuin kuvion 1, mutta lohkoalgebra tarjoaa sarjan yksinkertaisia ​​sääntöjä järjestelmäjärjestelmän manipuloimiseksi ja sen yksinkertaisimmaksi versioksi.

Kuten alussa selitetään, kaavio käyttää lohkoja, nuolia ja ympyröitä kunkin järjestelmän komponentin ja sen läpi kulkevien signaalien virtauksen välisen suhteen luomiseksi.

Block -algebra mahdollistaa kahden tai useamman signaalin vertaamisen summan, vähentämisen ja niiden kertomisen kautta sekä analysoida jokaisen komponentin panos järjestelmään.

Tämän ansiosta on mahdollista vähentää koko järjestelmä yhdeksi tulosignaaliksi, ainutlaatuinen siirtotoiminto, joka kuvaa kokonaan järjestelmän toimintaa ja vastaavaa lähtöä.

Se voi palvella sinua: Astroclymics: Historia, mitä tutkimuksia, sivukonttoreita

Estokaavion elementit

Lohkokaavion elementit ovat seuraavat:

Signaali

Signaalit ovat hyvin monipuolisia, esimerkiksi on yleistä, että se on sähkövirta tai jännite, mutta se voi olla kirkas, ääni ja paljon muuta. Tärkeää on, että se sisältää tietoa tietystä järjestelmästä.

Signaali merkitään isolla kirjaimella, jos se on muuttujan funktio s Laplace -muunnoksesta: x (s) (katso kuva 1) tai pienillä kirjaimilla, jos se perustuu aikaan t, kuten x (t).

Lohkokaaviossa tulosignaalia edustaa nuoli, joka on suunnattu lohkoon, kun taas lähtösignaali, joka on merkitty y (s) tai (t), on merkitty lähtevällä nuolella.

Sekä syöttö- että lähtösignaali ovat ainutlaatuisia ja osoite, jossa tietovirrat määritetään nuolen suunnan perusteella. Ja algebra on sama jommallakummalle kahdelle muuttujalle.

Kortteli

Lohkoa edustaa neliö tai suorakulmio (katso kuva 1), ja sitä voidaan käyttää toimintojen suorittamiseen tai siirtofunktion toteuttamiseen, jota yleensä merkitään Call -kirjaimella G. Tämä toiminto on matemaattinen malli, jolla järjestelmän tarjoama vastaus kuvataan ennen pääsysignaalia.

Siirtofunktio voidaan ilmaista ajankohtana t kuten g (t) tai muuttuja s kuten g (s).

Kun tulosignaali X (S) saapuu lohkoon, se kerrotaan siirtofunktiolla ja muuttuu lähtösignaaliksi y (s). Matemaattisesti se ilmaistaan ​​seuraavasti:

Ja (s) = x (s).G (s)

Samoin siirtofunktio on suhde lähtösignaalin Laplace -muunnoksen ja tulosignaalin Laplace -muunnon välillä, edellyttäen, että järjestelmän alkuolosuhteet ovat NULL:

G (s) = y (s) / x (s)

Summaus

Summaa tai kesää, symboloi ympyrä, jolla on risti. Sitä käytetään yhdistämään summat ja vähennysten mukaan kaksi tai useampia signaaleja. Signaalia symboloivan nuolen lopussa merkki + sijoitetaan suoraan, jos tämä signaali lisätään tai merkki - jos vähennetään.

Seuraavassa kuvassa on esimerkki kesän toiminnasta: Sinulla on tulosignaali X, johon signaaleja A ja B lisätään, saadaan seurauksena poistuminen ja joka algebrallisesti vastaa:

Voi palvella sinua: Pystysuora laukaus: Kaavat, yhtälöt, esimerkit

Y = x+a+b

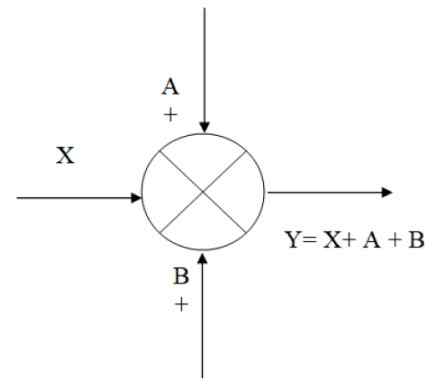Kuva 2. Esimerkki täytäntöönpanosta. Lähde: f. Zapata.

Haara

Sitä kutsutaan myös Haaroittumispiste. Siinä lohkosta tulee signaali jakautuu muihin lohkoihin tai putoon. Sitä edustaa signaalin nuolelle asetettu kohta ja siitä tulee toinen nuoli, joka ohjaa signaalin toista osaa kohti.

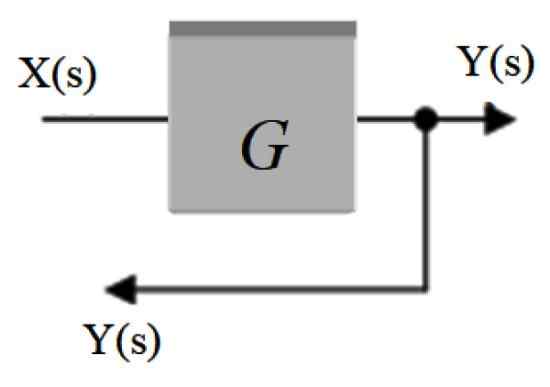Kuva 3. Haara. Lähde: f. Zapata.

Esimerkkejä lohkoalgebran lohkoista

Kuten aiemmin selitetään, ajatuksena on ilmaista järjestelmä lohkokaavion kautta ja vähentää sitä sitä kuvaavan siirtofunktion löytämiseksi. Seuraavat ovat lohkoalgebran säännöt kaavioiden yksinkertaistamiseksi:

Kaskadilohkot

Kun sinulla on signaali, joka kulkee peräkkäin G -lohkojen läpi₁, G₂, G₃..., se pelkistetään ainutlaatuiseksi lohkoksi, jonka siirtofunktio on G: n tuote₁, G₂, G₃..

Seuraavassa esimerkissä signaali X (S) tulee ensimmäiseen lohkoon ja sen poistumiseen on:

JA₁(s) = x (s).G₁(S)

Kuva 4. Kaksi lohkoa vesiputouksessa. Lähde: f. Zapata.

Vuorostaan ​​ja₁(s) kirjoita G -lohko₂(S), jonka lähtö on:

JA₂(s) = x (s).G₁(S). G₂(S)

Menettely on voimassa n kaskadilohkoissa:

JA_n (s) = x (s). G₁(S).G₂(S) ... g_n(S)

Lohkot rinnakkain

Vasemmassa kaaviossa X (S) -signaali Bifurca syöttää G -lohkot₁(S) ja g₂(S):

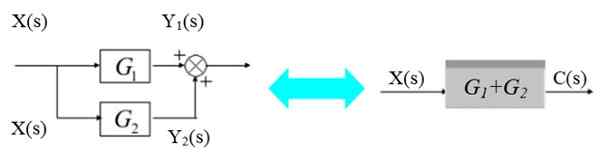Kuva 5. Kaksi lohkoa rinnakkain. Lähde: f. Zapata.

Vastaavat lähtösignaalit ovat:

JA₁(s) = x (s).G₁(S)

JA₂(s) = x (s).G₂(S)

Nämä signaalit lisätään:

C (s) = y₁(s) +₂(s) = x (s).[G₁(s) + g₂(s)]

Kuten oikeassa oikeassa kaaviossa esitetään.

Siirrä tarkistaja vasemmalle

Kesä voi siirtyä lohkon vasemmalle seuraavasti:

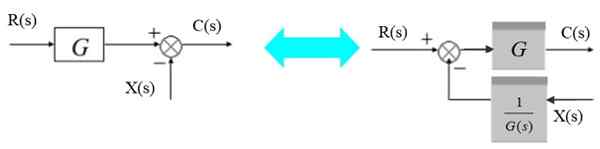Kuva 6. Siirrä lisäosa lohkon vasemmalle puolelle. Lähde: f. Zapata.

Vasemmalla lähtösignaali on:

C (s) = r (s). G (s) - x (s)

Vastaavasti oikealle:

C (s) = [r (s) - x (s)/g (s)]]]].G (s)

Siirrä oikealle oikealle

Kesä voi siirtyä lohkon oikealle puolelle näin:

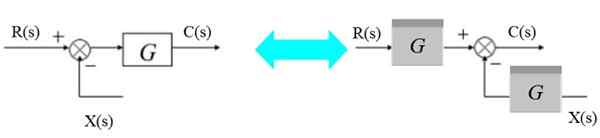Kuva 7. Siirrä tontti lohkon oikealla puolella. Lähde: f. Zapata.

Vasemmalla puolella sinulla on: [r (s) - x (s)].G (s) = c (s)

Voi palvella sinua: Archimedes Periaate: Kaava, esittely, sovellukset

Ja oikealla:

R (s). G (s) - x (s).G (s) = c (s)

Siirrä haaroittumispiste vasemmalta oikealle

Hajotuspisteen syrjäyttämiseksi lohkon vasemmalta oikealle puolelle riittää huomaamaan, että lähtö C (S) oikealle on tuote X (s).G (s). Kun haluat tulla uudelleen x (s), se kerrotaan g (s): n käänteellä.

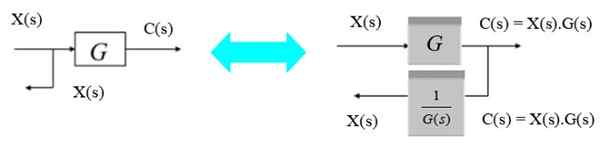Kuva 8. Siirrä haarapiste vasemmalta oikealle. Lähde: f. Zapata.

Siirrä haaroittumispiste oikealta vasemmalle

Vaihtoehtoisesti haaroittumispiste voi siirtyä oikealta vasemmalle seuraavasti:

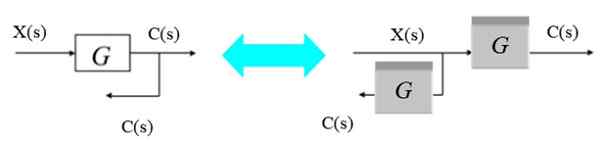Kuva 9. Siirrä haarapiste oikealta vasemmalle. Lähde: f. Zapata.

Koska haaroittumisen tulos haluaa saada C (s), uusi lohko G (S) on yksinkertaisesti välissä alkuperäisen lohkon vasemmalla puolella olevassa haaroittumispisteessä.

Järjestelmä palautteella

Seuraavassa järjestelmässä lähtösignaali C (S) syötetään vasemmalla olevan alistuvan kautta:

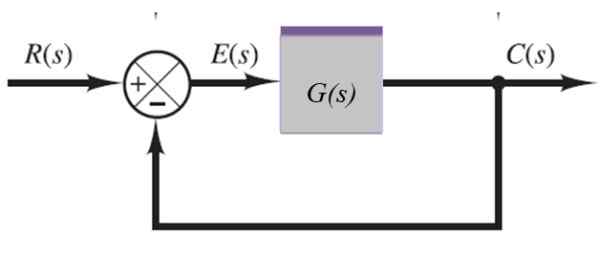Kuva 10. Järjestelmä palautteella. Lähde: f. Zapata.

C (s) = e (s).G (s)

Mutta:

E (s) = r (s) -c (s)

Tämän lausekkeen korvaaminen edellisessä yhtälössä on: c (s) = [r (s) -c (s)]]]].G (s), josta C (s) voidaan puhdistaa:

C (s) + c (s).G (s) = r (s).G (s) → C (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Tai vuorotellen:

C (s) / r (s) = g (s) / [1 + g (s)]]]

Graafisesti sen yksinkertaistamisen jälkeen on:

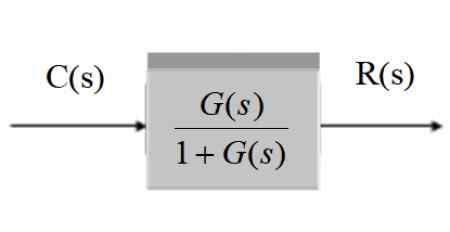Kuva 11. Järjestelmän yksinkertaistaminen palautteella. Lähde: f. Zapata.

Järjestelmä palautteella ja muuntajalla

Anturi koostuu siirtofunktiosta h (s):

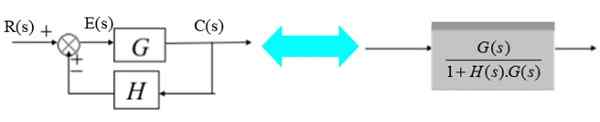Kuva 12. Järjestelmä palautteella ja muuntajalla. Lähde: f. Zapata.

Oikeassa kaaviossa lähtösignaali C (s) on:

C (s) = e (s). G (s) kanssa e (s) = r (s) - c (s).H (s)

Niin:

C (s) = [r (s) - c (s). H (s)]. G (s)

C (s) [1+ H).G (s)] = r (s).G (s)

Siksi C (s) voidaan puhdistaa:

C (s) = g (s).R (s) / [1+ h (s).G (s)]

Ja siirtotoiminto on:

G (s) / [1+ H (s).G (s)]

Kuten yksinkertaistetussa oikeassa kaaviossa esitetään.

Ratkaisut

Harjoitus 1

Etsi seuraavan järjestelmän siirtotoiminto:

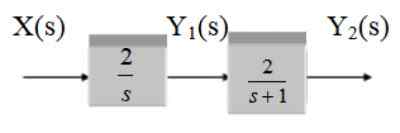Kuva 13. Kaksi lohkojärjestelmää vesiputouksessa. Lähde: f. Zapata.

Ratkaisu

Se on kaksi kaskadilohkoa, joten siirtofunktio on funktioiden g tuote g₁ ja g₂.

Sinun täytyy:

G₁ = 2/s

G₂ = 2 /(S+1)

Siksi haluttu siirtofunktio on:

G (s) = 4 / [S (S+1)]

Harjoitus 2

Vähennä seuraavaa järjestelmää:

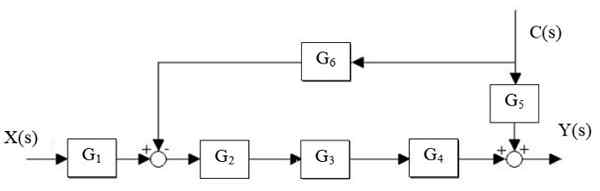Kuva 14. Järjestelmän yksinkertaistaminen. Lähde: f. Zapata.

Ratkaisu

Ensinnäkin G -kaskadi vähenee₂, G₃ ja g_4, Ja rinnakkainen G on erotettu₅ ja g₆-

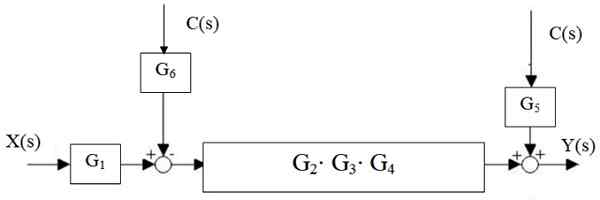Kuva 15. Vesiputousvähennys. Lähde: f. Zapata.

Sitten G -lohkon vasemmalla puolella oleva tarkastaja₂ ⋅G₃ ⋅ g₄ Hän liikkuu oikealle:

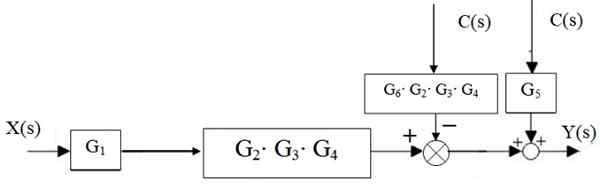Kuva 16. Järjestelmänvalvojan siirto. Lähde: f. Zapata.

Oikean kesät pelkistetään yhdeksi, samoin kuin kaskadilohkot:

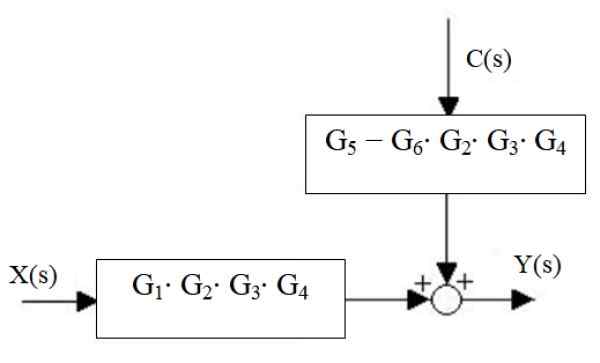Kuva 17. Uuden vesiputouksen ja oikean kesän vähentäminen. Lähde: f. Zapata.

Lopuksi järjestelmän lähtö on:

Ja (s) = x (s) ⋅g₁⋅ g₂ ⋅G₃ ⋅ g₄ + C (s) ⋅ [g₅ - G₆ ⋅ g₂ ⋅G₃ ⋅ g₄-

Viitteet

1. Alaydi, J. Järjestelmän lohkokaavion hallinta. Palautettu: sivustolta.iugaza.Edu.$.
2. Bolton, W. 2006. Valvontatekniikka. Toinen. Painos. Alfa -omega.
3. Cwalinsky, J. Johdatus järjestelmäsaltoalgebralle. Toipunut: cedEngineering.com.
4. Dademuchconnection. Lohkokaavio. Toipunut: Dademuch.com.
5. Ogata, k. 2010. Moderni valvontatekniikka. Viides. Painos. Pearson.