Fermat -raja koostuu ja harjoitukset ratkaistiin

Hän Fermat -raja Se on numeerinen menetelmä, jota käytetään linjan kaltevuuden arvon saavuttamiseen, joka on tangentti sen alueen tietylle funktiolle. Sitä käytetään myös funktion kriittisten pisteiden saamiseksi. Hänen ilmaisunsa on määritelty seuraavasti:

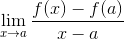
On selvää, että Fermat ei tiennyt johdannaisen perusteita, mutta hänen tutkimuksensa edisti matemaatikkojen ryhmää tiedustelemaan tangenttilinjoja ja heidän sovelluksiaan laskelmassa.

[TOC]

Mikä on Fermatin raja?

Se koostuu 2 pisteestä.

Kun lähestyt muuttujaa “A” -arvoon, pistepari on velvollinen tapaamaan. Tällä tavalla aiemmin kuivausviivasta tulee tangentti pisteeseen (a; f (a)).

Jakoarvo (x - A), kun arvioidaan kohdassa “A”, heittää tyypin K rajojen määrittelemättömyyden nollan (k/0) välillä (k/0). Missä nämä määrittelemät voidaan rikkoa erilaisten tekijätekniikoiden avulla.

Eniten käytettyjä toimintatekniikoita ovat:

-Neliöero (a² - b -² ) = (a + b) (a - b); Elementin olemassaolo (A-B) tarkoittaa suuressa osassa tapauksia, jotka tekijä, joka yksinkertaistaa ekspressiota (X-A) Fermat-rajasuhteessa.

- Neliön valmistuminen (kirves² + bx); Suorituksen jälkeen saadaan Newton Binomial, jossa yksi sen kahdesta tekijästä yksinkertaistetaan lausekkeella (x - a), rikkoen määrittelemättömyyden.

- Konjugaatti (a + b) / (a ​​+ b); Kerro ja jaa ekspressio jonkin tekijän konjugaatin avulla voi olla suurta apua määrittelemättömyyden katkaisemiseksi.

- Yhteinen tekijä; Monissa tapauksissa Fermat F (x) - F (a) -kertoimen osoitinta tekijään (x - a) tarvittava tekijä (x - a) tarpeen mukaan. Tätä varten havaitaan huolellisesti, mitkä elementit toistetaan jokaisessa ekspression tekijässä.

Voi palvella sinua: kuinka monta kymmenesosaa on yksikössä?

Fermat -raja -sovellus maksimiin ja minimiin

Jopa silloin, kun Fermatin raja ei eroa maksimin ja minimin välillä.

Perustiedot funktioiden graafisesta teoriasta tämän lauseen kanssa voittamisessa voi olla riittävä määrittämään maksimiarvot ja minimiarvot toimintojen välillä. Itse asiassa käännepisteet voidaan määritellä Fermatin lauseen ylimääräisen keskimääräisen arvon lauseella.

Kuutio vertaus

Ferman merkittävin paradoksi tuli tutkiessaan kuutiomaista vertausta. Koska hänen huomionsa oli suunnattu tietyn pisteen funktion tangenttiviivoihin, hän kohtasi mainitun tangenttiviivan määrittelemisen ongelman funktion nykyisessä käännekohdassa.

Näytti mahdotonta määrittää tangenttiviivaa pisteeseen. Siten alkaa kysely, joka aiheuttaisi differentiaalilaskennan. Sitten määritellään tärkeät matematiikan eksponentit.

Maximus ja minimaalinen

Funktion maksimin ja vähimmäismäärä oli haaste klassiselle matematiikoille, joissa näiden määritelmä on yksiselitteinen ja käytännöllinen menetelmä.

Fermat loi menetelmän, joka perustuu pienten differentiaalisten arvojen toimintaan, jotka tekijäprosessien jälkeen poistetaan antamalla tien eniten ja minimaaliseen arvoon.

Tämä muuttuja on arvioitava alkuperäisessä ekspressiossa mainitun pisteen koordinaatin määrittämiseksi, jotka yhdessä analyyttisten kriteerien kanssa määritellään ekspression maksimiarvolla tai minimillä.

Menetelmä

Menetelmässään Fermat käyttää Villan kirjaimellista symbolismia, joka koostui pääomakirjeiden yksinoikeudesta: vokaalit, tuntemattomat ja tunnettujen määrien konsonantit.

Voi palvella sinua: Rinnakkaispiped

Radikaalien arvojen tapauksessa Fermat toteutti tietyn prosessin, jota käytettäisiin myöhemmin määrittelemättömyysrajojen tekijöissä äärettömyys.

Tämä prosessi koostuu kunkin lausekkeen jakamisesta käytetyllä differentiaalisella arvolla. Fermat käyttivät E -kirjainta, jossa E: n suurimman voiman välisen jakautumisen jälkeen kriittisestä kohdasta tulee selvää.

Historia

Ferman raja on itse asiassa yksi vähiten tunnetuista panoksista matemaatikkojen pitkässä luettelossa. Hänen opintonsa olivat ensisijaisista lukumääristä, jotta voidaan luoda pohjimmiltaan laskenta.

Fermat puolestaan ​​tunnettiin epäkeskeisyydestään hypoteeseihinsa. Se oli yleistä eräänlaiselle haasteelle muille tuolloin matemaatikoille, kun hänellä oli jo ratkaisu tai esittely.

Sillä oli laaja valikoima riitoja ja liittoja tuolloin erilaisten matemaatikkojen kanssa, jotka rakastivat tai vihaavat työskentelyä hänen kanssaan.

Hänen viimeinen lauseensa oli tärkein vastuussa hänen maailmankuuluvuudestaan, jossa hän sanoi, että yleistys Pythagoras -lause Minkä tahansa "N" -asteen osalta se oli mahdotonta. Sanottiin olevan pätevä esittely siitä, mutta kuoli ennen sen julkistamista.

Tämän mielenosoituksen piti odottaa noin 350 vuotta. Vuonna 1995 Matemaatikot Andrew Wiles ja Richard Taylor päättivät Fermatin jättämän ahdistuksen osoittaen, että hän oli oikeassa hänen viimeisen lauseensa pätevässä osoituksessa.

Harjoitukset

Harjoitus 1

Määritä viivan kaltevuus tangentti käyrään f (x) = x² Vaiheessa (4, 16)

Korvaaminen fermatin rajan ilmaisussa:

Voi palvella sinua: täydellinen neliömäinen trinomial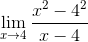

Sitten neliömäisten vähimmäismäärien käyttäjä on tekijä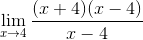

Tekijöitä yksinkertaistetaan (x - 4)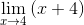

Arvioitaessasi sinulla on

M = 4 + 4 = 8

Harjoitus 2

Määritä lausekkeen kriittinen piste f (x) = x² + 4x käyttämällä Fermat -rajaa

Tässä tapauksessa koordinaattia ei ole, joten x -arvo korvataan yleisellä muodolla X_{0 -}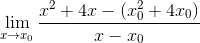

Suoritetaan strateginen ryhmittely, joka pyrkii ryhmittelemään X-X-ikätoverit_{0 -}

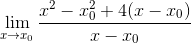
Neliöt kehitetään

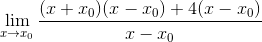
Yleinen tekijä X-X havaitaan_{0 ja se on uutettu}

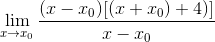
Ilmaisua voidaan jo yksinkertaistaa ja määrittelemätön on rikki

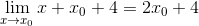
Vähimmäispisteissä tiedetään, että tangenttiviivan kaltevuus on yhtä suuri kuin nolla. Tällä tavoin voimme sovittaa nolla löydetyn lausekkeen ja tyhjentää x -arvon_{0 -}    

2 x_{0 -} + 4 = 0

X_{0 -} = -4/2 = -2

Puuttuvan koordinaatin saamiseksi sinun on arvioitava vain alkuperäisen toiminnon kohta

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Kriittinen kohta on P (-2, -4).

Viitteet

1. Todellinen analyysi. Historiallinen lähestymistapa Sauhl Stahl, John Wiley & Sons, 5. elokuuta. 1999.
2. Pierren matemaattinen ura Fermat, 1601-1665: toinen painos. Michael Sean Mahoney. Princeton University Press, 5. kesäkuuta. 2018
3. Fermatista Minkowskiin: Luennot lukujen teoriasta ja sen historiallisesta kehityksestä. W -. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Fermatin viimeinen lause: geneettinen johdanto algebralliseen lukuteoriaan. Harold M. Edwards. Springer Science & Business Media, 14. tammikuuta. 2000
5. FERMAT -päivät 85: Optimointia koskeva matematiikka. J -.-B -. Hiriart-Uruty Elsevier, 1. tammikuuta. 1986