Kohtisuora linjan ominaisuudet, esimerkit, harjoitukset

Eräs kohtisuora Se muodostaa 90º kulman toiseen viivaan, käyrään tai pintaan. Huomaa, että kun kaksi riviä ovat kohtisuorassa ja samalla tasolla, kun ne on leikattu, ne muodostavat neljä identtistä kulmaa, jokainen 90º.

Jos yksi kulmista ei ole 90º, sanotaan, että linjat ovat vinoja. Kohtisuorat viivat ovat usein suunnittelussa, arkkitehtuurissa ja rakentamisessa, esimerkiksi seuraavan kuvan putkiverkko.

Kuvio 1. Suora -putki ja lukuisat kohtisuorat viivat. Kuinka monta 90º kulmaa voidaan laskea tässä kuvassa? Lähde: Piqsels.

Kohtisuorien viivojen suunta voi olla monipuolinen, kuten alla esitetyt:

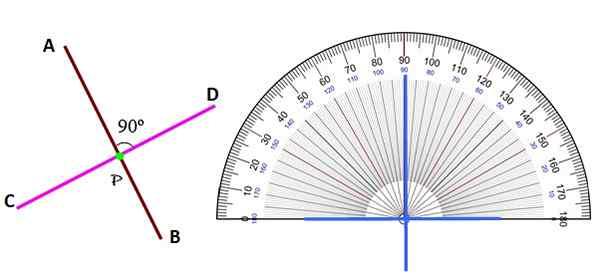
Kuva 2. Kohtisuora viivat tasossa. Lähde: f. Zapata.

Kohdasta riippumatta kohtisuorat viivat tunnistetaan tunnistamalla niiden välinen kulma 90º: ksi kuljettimen avulla.

Huomaa, että toisin kuin tason yhdensuuntaiset viivat, jotka eivät ole koskaan leikkaa, kohtisuorassa tehdään aina pisteessä P, nimeltään jalka yhden linjan toisesta. Siksi myös kaksi kohtisuoraa viivaa on Secantes.

Mikä tahansa linja on ääretön kohtisuorassa siihen, koska vain siirtämällä AB -segmentti vasemmalle tai oikealle CD -segmenttiin, meillä on uusi kohtisuorassa toisen jalan kanssa.

Kuitenkin kohtisuoraa, joka kulkee vain segmentin keskipisteen läpi puolustaja mainitun segmentin.

[TOC]

Esimerkkejä kohtisuorista viivoista

Kohtisuorat viivat ovat usein kaupunkimaisemassa. Seuraavassa kuvassa (kuva 3) vain muutama monista kohtisuorista viivoista, joita arvostetaan tämän rakennuksen yksinkertaisella julkisivulla ja sen elementeillä, kuten ovet, kanavat, vaiheet ja paljon muuta: lisää:

Voi palvella sinua: Fourier Diskreet Transformated: Ominaisuudet, sovellukset, esimerkit Kuva 3. Tällaisen yhteisen rakennuksen julkisivulla on paljon kohtisuoria linjoja. Lähde: Richard Kang Flickrin kautta.

Hyvä asia on, että kolme riviä kohtisuorassa toisiinsa auttavat meitä luomaan pisteiden ja esineiden sijainnin avaruudessa. Ovat koordinaattiakselit tunnistettu X -akseli, Akseli y ja Z -akseli, Selvästi näkyvissä suorakulmaisen huoneen kulmassa, kuten seuraavat:

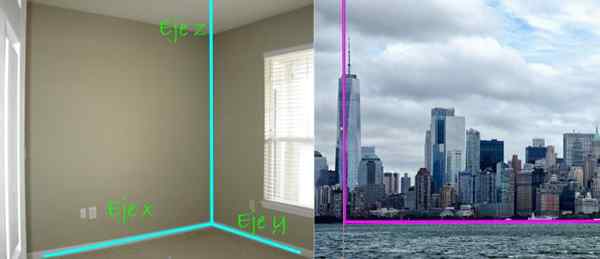Kuva 4. Cartesian Axis -järjestelmä koostuu kolmesta viivasta kohtisuorassa toisiinsa nähden, jokaisella on etusija -avaruussuunta avaruudessa. Vasen kuvahyvitykset: Treybunn 2 kautta Flickr. Oikea kuva; Needpix.

Panoraamanäkymässä kaupungista, oikealla puolella, luisakerrosten ja maan väliset kohtisuorat varoitetaan. Ensimmäinen sanoisi, että se löytyy koko Z -akseli, Vaikka maa on taso, joka tässä tapauksessa on taso Xy.

Jos maa muodostaa tason Xy, Pilvenpiirtäjä on myös kohtisuorassa mihin tahansa kadulle tai kadulle, mikä takaa sen vakauden, koska kalteva rakenne on epävakaa.

Ja kaduilla, missä tahansa suorakaiteen muotoisia kulmia, on kohtisuora viivoja. Monilla tavoilla ja kaduilla on kohtisuora asettelu, edellyttäen, että maa- ja maantieteelliset onnettomuudet sallivat sen.

Käytetään viivojen, segmenttien tai vektorien välisen kohtisuorisuuden ilmaisemiseksi, symbolia ⊥. Esimerkiksi, jos linja l₁ on kohtisuorassa linjaan L₂, me kirjoitimme:

Lens₁ ⊥ L₂

Lisää esimerkkejä kohtisuorista viivoista

- Suunnittelussa kohtisuorat viivat ovat hyvin läsnä, koska monet yleiset esineet perustuvat neliöihin ja suorakulmioihin. Näille kvadrilateriaaleille on tunnusomaista 90º sisäkulma, koska niiden sivut ovat kaksi tai kaksi yhdensuuntaista:

Se voi palvella sinua: Yleinen Parabola -yhtälö (esimerkit ja harjoitukset)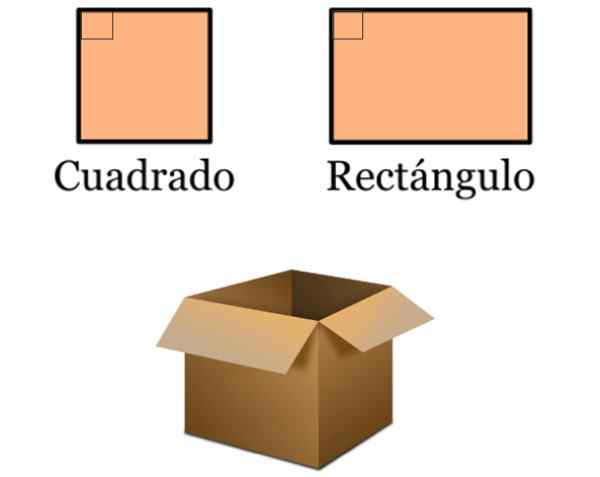 Kuva 5. Neliöt ja suorakulmiot ovat osa lukuisia malleja, kuten tämän yksinkertaisen pahvilaatikko tavaroiden säilyttämiseksi. Lähde: f. Zapata.

- Tuomioistuimet, joissa harjoitetaan erilaisia ​​urheilulajeja. Nämä puolestaan ​​sisältävät kohtisuorat viivat.

- Kaksi segmenttiä, jotka muodostavat suorakulmion kolmion, ovat kohtisuorassa toisiinsa. Näitä kutsutaan luokat, Vaikka jäljellä oleva linja kutsutaan hypotenuusa.

- Sähkökenttävektorilinjat ovat kohtisuorassa sähköstaattisen tasapainon pintaan nähden.

- Katautuneelle kuljettajalle laitteet ja laitteet ovat aina kohtisuorassa sähkökentän laitteisiin.

- Putkijärjestelmissä tai kanavissa, joita käytetään erilaisten nesteiden, kuten kaasun, kuljettamiseen, jotka ilmestyvät kuvassa 1, on yleistä, että kyynärpäät ovat suorassa kulmassa. Siksi ne muodostavat kohtisuorat viivat, kuten kattilahuoneessa:

Kuva 6. Putket kattilahuoneessa. Lähde: Wikimedia Commons. Roger mclassus/cc by-s (http: // creativecommons.Org/lisenssit/by-SA/3.0/)

Harjoitukset

- Harjoitus 1

Piirrä kaksi kohtisuoraa viivaa säännön ja kompassin mukaan.

Ratkaisu

Näiden vaiheiden noudattaminen on hyvin helppoa:

-Ensimmäinen rivi on piirretty, nimeltään AB (musta).

-AB -merkinnän p: n yläpuolella (tai alhaisempi) yläpuolella, missä kohtisuorassa on. Jos P on juuri AB: n puolet yläpuolella (tai alle), kohtisuorassa on AB -segmentin puolustaja.

-Kun kompassi on keskittynyt P: hen, piirretään ympyrä, joka leikkaa AB: n kahdessa pisteessä, kutsutaan 'ja b' (punainen).

Voi palvella sinua: Ystävälliset tai ystävälliset numerot: Esimerkkejä ja kuinka löytää ne

-A'P: n kompassi avataan, se keskittyy 'ja piirretään ympyrä, joka kulkee P (vihreän) läpi.

-Toista edellinen vaihe, mutta avaa nyt kompassin B'P -segmentin pituus (vihreä). Molemmat kehäkaarit leikataan pisteessä Q alapuolella p ja tietysti jälkimmäisessä.

-Pisteet P ja Q yhdistetään sääntöyn ja kohtisuora viiva (sininen) on jo valmis.

-Lopuksi kaikki apurakenteet on poistettava huolellisesti, jättäen vain kohtisuoraan.

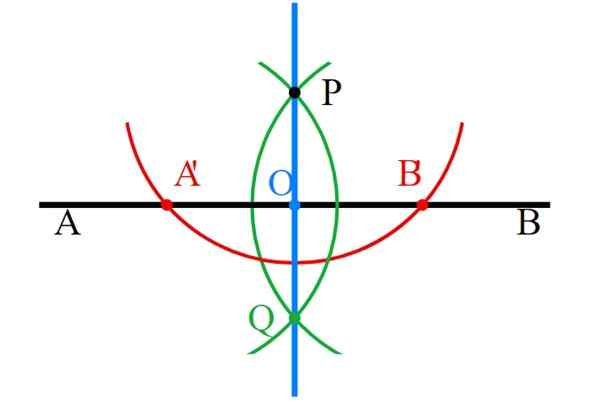Kuva 6. Siirtymäviivat säännön ja compassin kanssa. Lähde: Wikimedia Commons.

- Harjoitus 2

Kaksi riviä l₁ ja minä₂ Ne ovat kohtisuorassa, jos heidän vastaavat rinteet m₁ ja m₂ He täyttävät tämän suhteen:

m₁ = -1/m₂

Kun otetaan huomioon viiva y = 5x - 2, etsi sille kohtisuora viiva ja läpäise pisteen (-1, 3).

Ratkaisu

-Ensinnäkin on kohtisuoran viivan m kaltevuus_⊥, Kuten lausunnossa todetaan. Alkuperäisen viivan kaltevuus on M = 5, "x" mukana oleva kerroin. Niin:

m_⊥= -1/5

-Sitten kohtisuoran viivan yhtälö on rakennettu ja_⊥, Aikaisemmin löydetyn arvon korvaaminen:

ja_⊥= -1/5x + b

-Sitten määritetään B: n arvo lausunnon (-1,3) annetun pisteen avulla, koska kohtisuoran viivan on läpäistävä sen läpi:

y = 3

x = -1

Korvaus:

3 = -1/5 (-1) + B

B: n arvo tyhjennetään:

B = 3- (1/5) = 14/5

-Lopuksi lopullinen yhtälö on rakennettu:

ja_⊥= -1/5x + 14/5

Viitteet

1. Baldor, a. 2004. Litteä ja avaruusgeometria. Kulttuurijulkaisut.
2. Clemens, S. 2001. Geometria sovellusten ja ongelmanratkaisun kanssa. Addison Wesley.
3. Matematiikka on hauskaa. Kohtisuoraviivat. Toipunut: Mathisfun.com.
4. Monterey Institute. Kohtisuoraviivat. Toipunut: Montereyinstitute.org.
5. Wikipedia. Kohtisuoraviivat. Palautettu: on.Wikipedia.org.