Diskreetti matematiikka

Mitkä ovat erillinen matematiikka?

Se diskreetti matematiikka vastaa matematiikan aluetta, joka vastaa luonnollisten lukujen joukon tutkimisesta; eli rajalliset ja äärettömät kirjanpidonumerot, joissa elementit voidaan laskea erikseen, yksi kerrallaan.

Nämä sarjat tunnetaan erillisinä sarjoina; Esimerkki näistä sarjoista on kokonaisia ​​numeroita, kuvaajia tai loogisia lausekkeita, ja niitä sovelletaan eri tieteen aloilla, pääasiassa tietotekniikassa tai tietojenkäsittelyssä.

Kuvaus

Diskreetti matematiikassa prosessit ovat lukutasoisia, ne perustuvat koko numeroihin. Tämä tarkoittaa, että desimaalilukuja ei käytetä, joten lähestymistapaa tai rajoja, kuten muilla alueilla, ei myöskään käytetä. Esimerkiksi tuntematon voi olla yhtä suuri kuin 5 tai 6, mutta ei koskaan 4,99 tai 5.9.

Toisaalta, graafisessa esityksessä muuttujat ovat erillisiä ja ne annetaan äärellisestä pistejoukosta, jotka lasketaan yksi kerrallaan, kuten kuvassa havaitaan:

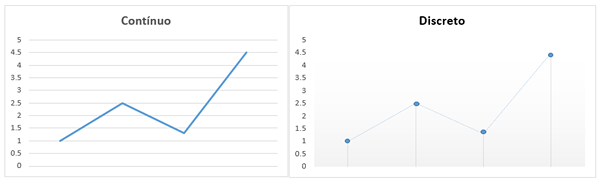
Diskreetti matematiikka syntyy tarpeen saada tarkka tutkimus, joka voidaan yhdistää ja todistaa sen soveltamiseksi eri alueilla.

Mitä on erillinen matematiikka?

Diskreetistä matematiikkaa käytetään useilla alueilla. Tärkeimpien joukossa ovat seuraavat:

Yhdistelmä-

Tutki äärellisiä sarjoja, joissa elementit voidaan tilata tai yhdistää ja palauttaa.

Erillinen jakeluteoria

Tutkimustapahtumia, joita esiintyy tiloissa, joissa näytteet voivat olla kirjanpitoa, joissa jatkuvia jakaumia käytetään diskreettien jakaumien lähestymiseen tai päinvastoin.

Tietoteoria

Se viittaa tietokoodaukseen, jota käytetään tietojen suunnitteluun ja lähettämiseen sekä tallentamiseen, kuten vastaaviin signaaleihin.

Voi palvella sinua: Trachtenberg -menetelmä: Mikä se on, esimerkkejä

Laskenta

Matematiikan avulla ongelmat ratkaistaan ​​algoritmeilla, samoin kuin mitä voidaan laskea ja sen tekemiseen tarvittava aika (monimutkaisuus).

Diskreetti matematiikan merkitys tällä alueella on lisääntynyt viime vuosikymmeninä, etenkin ohjelmoinnin kehittämisessä ja Softwares.

Sala

Se perustuu hienovaraiseen matematiikkaan turvallisuusrakenteiden tai salausmenetelmien luomiseksi. Esimerkki tästä sovelluksesta on salasanoja, jotka lähettävät erillisiä bittejä, jotka sisältävät tietoja.

Tutkimuksen kautta kokonaislukujen ja alaryhmien (numeroiden teoria) ominaisuudet voidaan luoda tai tuhota.

Logiikka

Käytetään erillisiä rakenteita, jotka yleensä muodostavat äärellisen sarjan lauseiden osoittamiseksi tai esimerkiksi ohjelmiston tarkistamiseksi.

Kaavioteoria

Se mahdollistaa loogisten ongelmien resoluution käyttämällä solmuja ja viivoja, jotka muodostavat kuvaajan tyypin, kuten seuraavassa kuvassa on esitetty:

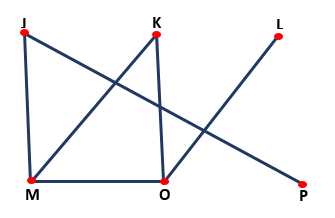Algebra

Se on alue, joka on läheisesti sidoksissa hienovaraiseen matematiikkaan, koska algebralliset ilmaisut ovat hienovaraisia. Tämän elektronisten piirien, prosessorien, ohjelmoinnin (Boolen algebran) ja tietokantojen (relaatioalgebra) kautta kehitetään (relaatioalgebra).

Geometria

Tutki geometristen objektien, kuten tason päällysteen, yhdistelmäominaisuuksia. Toisaalta laskennallinen geometria mahdollistaa geometristen ongelmien kehittämisen soveltamalla algoritmeja.

Asettaa teoria

Diskreettisen matematiikan joukossa (äärellinen ja ääretön tuntematon) ovat päätavoite. George Cantor julkaisi sarjan teorian, joka osoitti, että kaikki äärettömät sarjat ovat samankokoisia.

Sarja on joukko elementtejä (numerot, asiat, eläimet ja ihmiset, jotka ovat hyvin määriteltyjä; toisin sanoen on suhde, jonka mukaan kukin elementti kuuluu joukkoon, ja se ilmaistaan ​​esimerkiksi ∈ A.

Voi palvella sinua: tasa -arvon ominaisuudet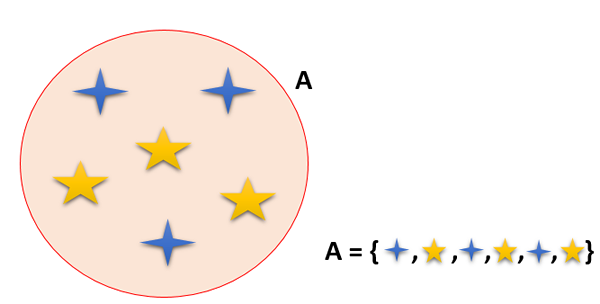

Matematiikassa on erilaisia ​​sarjoja, jotka ryhmittelevät tiettyjä numeroita niiden ominaisuuksien mukaan. Siten heillä on esimerkiksi:

- Luonnollisten lukujen sarja n = 0, 1, 2, 3, 4, 5, 6,… +∞.

- Kokonaislukujen sarja e = -∞…, -3, -2, -1, 0, 1, 2, 3,… +∞.

- Rationaalisten numeroiden alajoukko Q* = -∞…, - ¼, - ½, 0, ¼, ½,… ∞.

- REAL -lukujen sarja r = -∞…, -½, -1, 0, ½, 1,… ∞.

Sarjat on nimetty aakkoskirjeillä, isoilla kirjaimilla; Vaikka elementit on nimetty pienissä kirjaimissa, avaimet () ja erotettu pilkuilla (,). Niitä on yleensä esitetty kaavioissa, kuten Venn ja Caroll, sekä laskennallisesti.

Perusoperaatioiden, kuten unionin, risteyksen, komplementin, eron ja kartesiantuotteen, kanssa, sarjoja ja niiden elementtejä hallitaan kuulumisuhteen perusteella.

Sarjoja on monenlaisia, tutkittuja erillisissä matematiikassa ovat seuraavat:

Rajallinen sarja

Se on rajallinen määrä elementtejä ja joka vastaa luonnollista lukua. Siten esimerkiksi a = 1, 2, 3,4 on äärellinen sarja, jossa on 4 elementtiä.

Ääretön kirjanpitojoukko

Se on yksi, jossa on vastaavuus joukon elementtien ja luonnollisten lukujen välillä; Eli elementistä kaikki sarjan elementit voidaan luetella peräkkäin.

Tällä tavoin jokainen elementti vastaa luonnollisten lukujen jokaista elementtiä. Esimerkiksi:

Koko kokonaisluku z = … -2, -1, 0, 1, 2… voidaan luetella nimellä z = 0, 1, -1, 2, -2…. Tällä tavoin on mahdollista tehdä yksi -yksi -vastaavuus z: n ja luonnollisten lukujen välisten elementtien välillä, kuten seuraavassa kuvassa voidaan nähdä:

Voi palvella sinua: lähestymistapojen laskeminen erottelujen avulla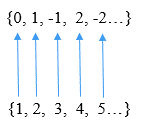

Harkinnanvara

Se on menetelmä, jota käytetään jatkuvien ongelmien ratkaisemiseen (mallit ja yhtälöt), jotka on muunnettava erillisiksi ongelmiksi, joissa ratkaisu tunnetaan lähestymistavan jatkuvan ongelman ratkaisuun.

Muuten havaitseminen yrittää saada rajallisen määrän äärettömiä pisteitä; Tällä tavoin jatkuva yksikkö muutetaan yksittäisiksi yksiköiksi.

Yleensä tätä menetelmää käytetään numeerisessa analyysissä, kuten differentiaaliyhtälön liuoksessa, funktion kautta, jota edustaa rajallinen määrä tietoja sen alueella, vaikka tämä on jatkuvaa.

Toinen esimerkki diskreisoinnista on sen käyttö digitaalisen signaalin analogisen muuntamiseen, kun jatkuvat signaaliyksiköt muunnetaan yksittäisiksi yksiköiksi (ne diskreisoidaan) ja sitten koodataan ja kvantifioidaan digitaalisen signaalin saamiseksi, jotta saadaan aikaan digitaalinen signaali.

Viitteet

1. Grimaldi, r. P. (1997). Erillinen ja yhdistelmä matematiikka. Toimitus Addison Wesley Iberoamericana.
2. Ferrando, V. Gregori. (tuhatyhdeksänsataayhdeksänkymmentäviisi). Diskreetti matematiikka. Palautus.
3. Jech, t. (2011). Asettaa teoria. Stanfordin filosofian tietosanakirja.
4. José Francisco Villalpando Becerra, a. G. (2014). Erillinen matematiikka: sovellukset ja harjoitukset. Patria -toimitusryhmä.
5. Landau, r. (2005). Laskenta, ensimmäiseen tieteelliseen kurssiin.
6. Merayo, f. G. (2005). Diskreetti matematiikka. Thomson -toimitus.
7. Rosen, k. H. (2003). Erillinen matematiikka ja sen sovellukset. McGraw-Hill-toimitus.
8. Schneider, D. G. (tuhatyhdeksänsataayhdeksänkymmentäviisi). Looginen lähestymistapa erilliseen matematiikkaan.