Käänteinen matriisilaskelma ja harjoitus ratkaistu

Se Käänteinen matriisi Tietyn matriisin mukaan matriisi kerrottuna alkuperäisillä tuloksilla identiteettimatriisiin. Käänteinen matriisi on hyödyllinen lineaaristen yhtälöiden järjestelmien ratkaisemisessa, joten sen laskemisen tärkeys on tärkeää.

Matriisit ovat erittäin hyödyllisiä fysiikassa, tekniikassa ja matematiikassa, koska ne ovat kompakti työkalu monimutkaisten ongelmien ratkaisemiseksi. Matriisien hyödyllisyys paranee, kun ne ovat kääntäviä ja myös niiden käänteinen.

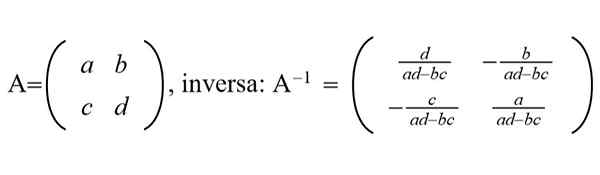Kuvio 1. Yleinen 2 × 2 -matriisi ja sen käänteinen matriisi on esitetty. (Valmistaja Ricardo Pérez)

Graafisessa prosessointikentässä Big Data, tiedon louhinta, koneoppiminen ja muut käytetään tehokkaita ja nopeita algoritmeja NXN -matriisien käänteisen matriisin arvioimiseksi N: n erittäin suurella, tuhansien tai miljoonien järjestyksessä.

Käänteisen matriisin käytön havainnollistamiseksi lineaaristen yhtälöiden järjestelmän hallinnassa aloitamme kaikkien yksinkertaisimmalla tapauksella: 1 × 1 matriisit.

Yksinkertaisin tapaus: Yhden muuttujan lineaarinen yhtälö otetaan huomioon: 2 x = 10.

Ajatuksena on löytää x: n arvo, mutta se on "matrixly". 

Matriisi M = (2), joka kertoo vektorista (x), on 1 × 1 -matriisi, joka johtaa vektoriin (10):

M (x) = (10)

M -matriisin käänteinen merkitsee M: llä^-1.

Yleinen tapa kirjoittaa tämä "lineaarinen järjestelmä" on:

M x = b, missä x on vektori (x) ja b on vektori (10).

Määritelmän mukaan käänteinen matriisi on yksi kerrottuna alkuperäisellä matriisilla identiteettimatriisi I:

M^-1 M = i

Matrix m^-1 Se on matriisi (½), eli m^-1 = (½) koska m^-1 M = (½) (2) = (1) = i

Voi palvella sinua: 90 jakajaa: Mitkä ovat ja selitys

Löydä tuntematon vektori x = (x) korotetussa yhtälössä molemmat jäsenet kerrotaan käänteisen matriisin avulla:

M^-1 M (x) = m^-1 (10)

(½) (2) (x) = (½) (10)

(½ 2) (x) = (½ 10)

(1) (x) = (5)

(x) = (5)

Kahden vektorin tasa -arvo on saavutettu, jotka ovat samat vain silloin, kun niiden vastaavat elementit ovat yhtä suuret, eli x = 5.

Matriisin käänteisen laskenta

Se, mikä motivoi käänteisen matriisin laskemista, on löytää universaali menetelmä lineaaristen järjestelmien, kuten seuraavan 2 × 2 -järjestelmän, ratkaisemiseksi:

x - 2 y = 3

-x + y = -2

Edellisessä osassa tutkittujen tapausten 1 × 1 vaiheiden seurauksena kirjoitamme yhtälöjärjestelmän matriisilla:

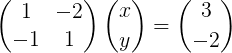Kuva 2. Lineaarinen järjestelmä matriisimuodossa.

Huomaa, että tämä järjestelmä on kirjoitettu kompakti vektorimerkinnällä seuraavasti:

M x = b

missä

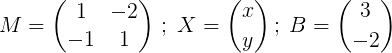
Seuraava vaihe on löytää m.

Menetelmä 1: Gaussin eliminaation kautta

Gaussin eliminointimenetelmää sovelletaan. Joka koostuu alkeisoperaatioiden tekemisestä matriisin riveissä, nämä operaatiot ovat:

- Kerro rivi ei -nollinnumerolla.

- Lisää tai vähennä toinen rivi tai toisen rivin monikerros.

- Vaihtaa rivejä.

Tavoitteena on näiden operaatioiden kautta alkuperäisen matriisin muuntaminen identiteettimatriisiksi. 

Kuten tämä on tehty. Kun useiden R -rivien operaatioiden jälkeen, se muuttuu yhtenäiseksi matriisiksi, silloin se, joka oli alun perin yhtenäinen, muuttuu M: n käänteiseen matriisiin, ts. M, M^-1.

Voi palvella sinua: seuraus (geometria)

1- Aloitamme prosessin kirjoittamalla Matrix M ja sen vieressä yksikkömatriisi:

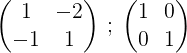
2- Lisäämme kaksi riviä ja tulos laitetaan toiseen riviin, tällä tavalla saamme nollan toisen rivin ensimmäisessä elementissä:

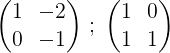
3- Kerrota toinen rivi -1: llä saadaksesi 0 ja 1 toisesta rivistä:

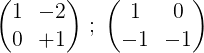
4- Ensimmäinen rivi kerrotaan ½: ½:

5- Toinen ja ensimmäinen lisää ja tulos asetetaan eturiviin:

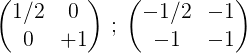
6- Prosessin lopettamiseksi ensimmäinen rivi 2 kerrottuna saadaan ensimmäisessä identiteettimatriisissa ja toisessa alkuperäisen matriisin m käänteinen matriisi:

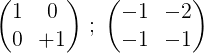
Tarkoittaen:

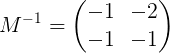
Järjestelmäratkaisu

Kun käänteinen matriisi on saatu, yhtälöjärjestelmä ratkaistaan ​​soveltamalla käänteistä matriisia kompaktin vektoriyhtälön molemmille jäsenille:

M^-1M x = m^-1B -

X = m^-1B -

Se pysyy nimenomaisesti näin:

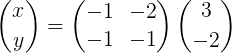
Sitten matriisin kertolasku tehdään vektorin x saamiseksi:

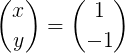
Menetelmä 2: Liitteenä matriisi

Tässä toisessa menetelmässä käänteinen matriisi lasketaan alkuperäisen matriisin kiinnittyneen matriisin perusteella -Lla.

Oletetaan, että matriisi on antanut:

minne_{minä, j} Se on rivin elementti Yllyttää ja pylväs J - matriisin -Lla.

Matriisin kiinnitys -Lla Sitä kutsutaan Adj (a) Ja sen elementit ovat:

ILMOITUS_{minä, j} = (-1)^(I+J) ¦ai, jdy

missä Ai, j Se on komplementaarinen pieni matriisi, joka saadaan poistamalla rivi I ja sarake J alkuperäisestä matriisista -Lla. Palkit ¦ ¦ osoittavat, että determinantti on laskettu, eli ¦ai, jdy Se on komplementaarisen vähäisen matriisin määräävä tekijä.

Voi palvella sinua: homologiset puolet

Käänteinen matriisikaava

Kaava käänteisen matriisin löytämiseksi alkuperäisen matriisin kiinnitetyn matriisin perusteella on seuraava:

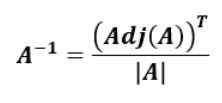
Eli käänteinen matriisi -Lla, -Lla^-1, on kiinnittymisen siirtäminen -Lla jaettu determinantilla -Lla.

Siirretty -Lla^Tmatriisin -Lla Se on se, joka saadaan vaihtamalla sarakkeiden rivejä, ts. Ensimmäisestä rivistä tulee ensimmäinen sarake ja toinen rivi toiseen sarakkeeseen ja niin edelleen, kunnes alkuperäisen matriisin N -rivit.

Liikuntaa

Ole matriisi seuraavaan:

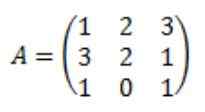
Jokainen A: adj (a): n kiinnitetyn matriisin elementti on laskettu

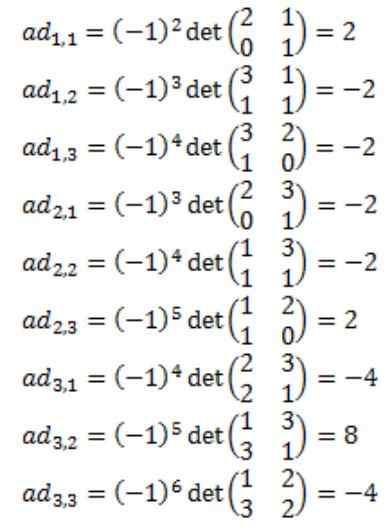
Tuloksena, että A, adj (a): n kiinnittynyt matriisi on seuraava:

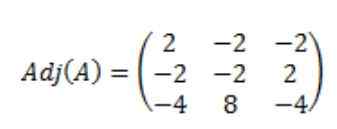
Sitten matriisin A, det (a) -sovelluksen determinantti lasketaan:

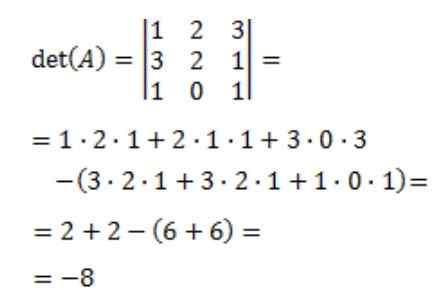
Lopuksi saadaan käänteinen matriisi:

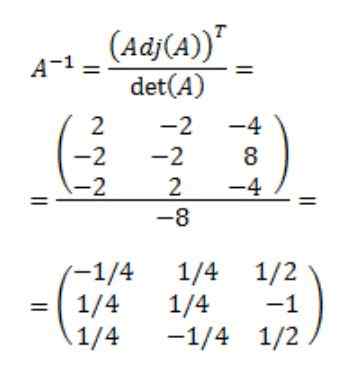
Viitteet

1. Anthony Nicolaides (1994) determinantit ja matriisit. Pass -julkaisu.
2. AWOL ASEN (2013) Tutkimus 3 x 3: n determinanttien laskennasta
3. Casteleiro Villalba m. (2004) Johdanto lineaariseen algebraan. ESIC -toimitus.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Matematiikka: Opiskelijan selviytymisopas. Cambridge University Press.
6. Richard J. Brown (2012) 30 sekunnin matematiikka: 50 mielenterveysteoriaa matematiikassa. Ivy Press Limited.
7. Matriisi. Lap Lambert Academic Publishing.