Amorfisten lukujen likimääräinen mittaus esimerkki ja liikunta

Se Likimääräinen mittaus Amorfisista hahmoista koostuu sarjasta menetelmiä, joita käytetään geometristen lukujen alueen tai kehän määrittämiseen, jotka eivät ole kolmioita, neliöitä, ympyröitä jne. Jotkut ovat laajennettavissa kolmeen dimensioiseen lukuun.

Pohjimmiltaan mittaus koostuu verkotuksen tekemisestä säännöllisesti, kuten suorakulmiot, neliöt tai trapetsoidit, jotka peittävät suunnilleen pinnan. Näillä menetelmillä saadun alueen lähestymistavan tarkkuus kasvaa reticulate -hienovaraisuuden tai tiheyden myötä.

Kuvio 1. Amorfisten hahmojen muotoisia kiviä. Lähde: PxFuel.

Kuviot 1 ja 2 esittävät erilaisia ​​amorfisia lukuja. Alueen laskemiseksi retikulate, joka koostuu 2 x 2 neliöstä, jotka puolestaan ​​jaotellaan kaksikymmentä viiteen neliöön 2/5 x 2/5.

Pää neliöiden ja sekundaaristen neliöiden lisääminen Amorfisen hahmon likimääräinen alue saadaan.

Kuva 2. Virheellinen, jotta voidaan laskea yhden amorfisen luvun pinta -ala likimääräisesti. Lähde: f. Zapata

[TOC]

Käyrän alla oleva alue

Kahden raja -arvon välillä on usein tarpeen laskea alue käyrän alla. Tässä tapauksessa neliömäisen retikulaatin sijasta suorakaiteen muotoiset raidat voidaan jäljittää suunnilleen mainitun käyrän alla olevasta alueesta.

Kaikkien suorakulmaisten raidojen summaa kutsutaan Riemannin summa tai summa. Kuvio 3 näyttää välin "a, a, b], jolla haluat määrittää suunnilleen käyrän alla olevan alueen.

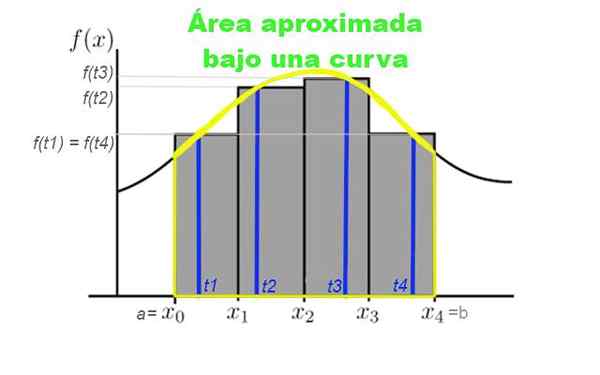Kuva 3. Väliaika [a, b] neljään alaluokkaan, jotka yleensä otetaan samasta leveydestä. Suorakulmioiden korkeus määritetään subintervalsiin kuuluvan TK: n käyrän arvon perusteella. Lähde: f. Zapata.

Oletetaan. Tätä varten tehdään N -elementtien osio:

Voi palvella sinua: 60 jakajaa

Osio = x0 = a, x1, x2, ..., xn = b.

Sitten likimääräinen alue, jonka y = f (x) on antanut aikavälillä [a, b], saavutetaan seuraavalla summalla:

S = ∑_{K = 1}ⁿ f (t_{k -k -}) (x_{k -k -} - x_K-1-A

Missä t_{k -k -} on välillä x_K-1 ja x_{k -k -}: x_K-1 ≤ t_{k -k -} ≤ x_{k -k -} .

Kuvio 3 esittää käyrän y = f (x): n riemannin summan [x0, x4]. Tässä tapauksessa tehtiin neljän subintervaalin jakautuminen ja summa edustaa harmaiden suorakulmioiden kokonaispinta -alaa. 

Tämä summa edustaa lähestymistapaa käyrän F abstantin alla olevalle alueelle Abscissas X = x0 ja x = x4: n välillä.

Lähestymistapa käyrän alla olevaan alueelle paranee siinä määrin kuin luku n osioista on suurempi, ja siinä on taipumus olla täsmälleen käyrän alla oleva alue, kun numero n osioilla on taipumus äärettömyyteen. 

Jos käyrä edustaa analyyttinen funktio, arvot F (T_{k -k -}) Ne lasketaan arvioimalla mainitun toiminnon arvoissa t_{k -k -}. Mutta jos käyrällä ei ole analyyttistä lauseketta, seuraavat mahdollisuudet ovat edelleen:

1. Lähestyä käyrää funktion avulla, esimerkiksi polynomi.
2. Ota pisteiden Cartesian koordinaatit, joissa käyrä sieppataan linjojen kanssa x = t_{k -k -}.

Säännöllisiä aikavälejä

TK -arvon valinnasta välein riippuen [x_{k -k -}, x_K-1], summa voi yliarvioida tai aliarvioida funktion käyrän alla olevan alueen tarkan arvon y = f (x). Suosituin asia on ottaa TK -piste, jolla puuttuva alue on suunnilleen yhtä suuri kuin jäljellä oleva alue, vaikka tällaista valintaa ei aina ole mahdollista tehdä.  

Voi palvella sinua: moninkertainen käänteinen: Selitys, esimerkit, ratkaisut harjoitukset

Ota TK lopussa

Käytännöllisin asia on sitten käyttää säännöllisiä väliajoja laajoista Δx = (b - a)/n, missä a ja b ovat abskissan minimi- ja maksimiarvoja, kun taas n on alajakojen lukumäärä.

Tällöin käyrän alla oleva alue lähestyy:

Pinta-ala = f (a+Δx)+f (a+2δx)+…+f [a+(n-1] Δx+f (b)*Δx

Edellisessä lausekkeessa TK otettiin alaryhmän oikeaan päähän.

Ota TK vasempaan päähän

Toinen käytännöllinen mahdollisuus on ottaa TK -arvo vasempaan päähän, jolloin alue, joka lähentää aluetta, ilmaistaan ​​seuraavasti:

Pinta-ala = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)*Δx

Tk keskusarvona

Jos TK valitaan Δx -leveyden tavanomaisen alaryhmän keskeiseksi arvoksi, käyrän alla oleva alue, joka lähestyy käyrän alla olevaa aluetta, on:

Pinta-ala = [f (a+Δx/2)+f (A+3AX/2)+…+F (B- Δx/2)]*Δx

Mikä tahansa näistä lausekkeista on taipumus tarkkaan, kun alajakojen lukumäärä on mielivaltaisesti suuri, toisin sanoen, että ΔX: llä on taipumus nolla, mutta tässä tapauksessa summan ehtojen lukumäärä on erittäin suuri seurauksena laskennallisilla kustannuksilla. 

Esimerkki

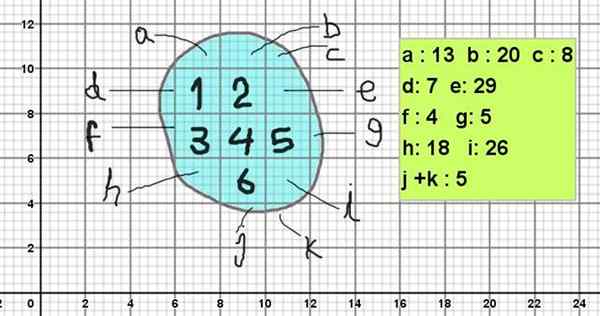
Kuvio 2 esittää amorfisen hahmon, jonka muoto on samanlainen kuin kuvan 1 kivet. Pinta -alan laskemiseksi se asetetaan retikulatelle, jossa päärakennukset ovat 2 x 2 yksikköä neliöön (esimerkiksi ne voivat olla 2 cm²).

Ja koska jokainen neliö on jaettu 5 x 5 -jakoihin, jokaisen alajaon pinta -ala on 0,4 x 0,4 neliöyksikköä (0,16 cm²).

Kuvion kuva lasketaan seuraavasti:

Voi palvella sinua: Yleinen tekijä: Esimerkkejä ja harjoituksia

Pinta -ala = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

Tarkoittaen:

Pinta -ala = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Liikuntaa

Laske suunnilleen funktion f (x) = x -käyrän alla oleva alue² Vetos a = -2 jopa b = +2. Tätä varten kirjoita summa, joka koskee säännöllisiä väliaikaisia ​​osioita [a, b] ja ota sitten matemaattinen raja tapaukselle, että osioiden lukumäärä yleensä äärettömyys. 

Ratkaisu

Ensinnäkin osioväli määritellään 

Δx = (b - a)/n. 

Sitten funktiota f (x) vastaavan oikean summa on tällainen:

A = -2 ja B =+2 korvataan siten, että aikaväli tai vaihe on Δx = 4/n. Tässä tapauksessa funktion f (x) = x summa² On:

 Neliöbinomi on kehitetty: 

[-2 +(4i/n)]² = 4 - 16 i /n + (4 /n)² Yllyttää²

Ja sitten se korvataan summana:

Yhteenvetojen erottaminen ja vakiomäärien ottaminen kunkin summan yleisenä tekijänä saadaan:

 Ensimmäinen summasta, toinen on:

Ja kolmas on:

Korvaaminen summan ilmaisussa:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Kun valitset suuren arvon N: lle, sinulla on hyvä lähestymistapa käyrän alla olevaan alueeseen. Tässä tapauksessa on kuitenkin mahdollista saavuttaa tarkka arvo, joka ottaa matemaattisen rajan, kun N: llä on taipumus äärettömyyteen:

Alue = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²-

Alue = 16 - (64/2)+ (64/3) = 16/3 = 5,333.

Viitteet

1. Casteleiro, J. M. 2002. Kattava laskelma (kuvitettu painos). Madrid: ESIC -toimitus.
2. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.
3. Purcell, E. 2007. Laskenta analyyttisellä geometrialla. 9NA. Painos. Pearson -koulutus.
4. Yksikaani. Integraalin käsitteen historia. Palautettu: arkistosta.Yksikaani.On
5. Uis. Riemann sumut. Toipunut: matematiikka.Uis.Edu.yhteistyö
6. Wikipedia. Alue. Palautettu: on.Wikipedia.com