Vaihtelevuusmittaukset

Kuvio 1.- Tunnetuimmat vaihtelumittaukset. Lähde: f. Zapata.

Mitkä ovat vaihtelevuusmittaukset?

Se Vaihtelevuusmittaukset, Kutsutaan myös dispersiomittareiksi, ne ovat tilastollisia indikaattoreita, jotka osoittavat, kuinka lähellä tai etäisyyttä niiden aritmeettisen keskiarvon tiedot löytyvät. Jos tiedot ovat lähellä keskiarvoa, jakauma on keskittynyt, ja jos ne ovat kaukana, se on sitten dispergoitu jakauma.

Tunnetuimpia on monia vaihtelevuusmittauksia: ovat:

• Etäisyys
• Keskimääräinen poikkeama
• Varianssi
• Keskihajonta

Nämä toimenpiteet täydentävät keskeisiä taipumusmittauksia ja ovat välttämättömiä saatujen tietojen jakautumisen ymmärtämiseksi ja poimia mahdollisimman paljon tietoa.

Etäisyys

Alue tai reitti mittaa tietojoukon amplitudin. Sen arvon määrittämiseksi havaitaan korkeimman arvon x välinen ero_max ja vähiten x -arvo_mini-

R = x_max - x_mini

Jos tiedot eivät ole löysät, vaan ryhmitelty aikavälillä, niin alue lasketaan viimeisen aikavälin ylärajan ja ensimmäisen aikavälin alarajan välillä eroavuudella.

Kun alue on pieni arvo, se tarkoittaa, että kaikki tiedot ovat melko lähellä toisiaan, mutta suuri alue osoittaa, että vaihtelua on paljon. On selvää, että datan ylärajan ja alarajan lisäksi alueella ei oteta huomioon niiden välillä, joten sitä ei ole suositeltavaa käyttää, kun datanumero on suuri.

Se on kuitenkin välitön toimenpide laskemiseen ja siinä on samat datayksiköt, joten se on helppo tulkita.

Esimerkki sijoituksesta

Seuraavaksi luettelo on saatavana viikonloppuna merkittyjen tavoitteiden lukumäärän kanssa yhdeksän maan jalkapalloliigoissa:

Voi palvella sinua: mitkä ovat 30? (Selitys)

40, 32, 35, 36, 37, 31, 37, 29, 39

Se on tietojoukko ryhmittelemättä. Alueen löytämiseksi he jatkavat tilaamaan ne vähiten suurimmaksi:

29, 31, 32, 35, 36, 37, 37, 39, 40

Korkein arvo, jolla on korkein arvo, on 40 tavoitetta ja alhaisin arvo on 29 tavoitetta, joten alue on:

R = 40–29 = 11 maalia.

Voidaan katsoa, ​​että alue on pieni verrattuna minimiarvotietoihin, mikä on 29 tavoitetta, joten voidaan olettaa, että datalla ei ole suurta vaihtelua.

Keskimääräinen poikkeama

Tämä variaatiomitta lasketaan poikkeamien absoluuttisten arvojen keskiarvon kautta keskiarvoon nähden. Merkitsee keskimääräistä poikkeamaa d_M, Ryhmittelemättömissä tiedoissa keskimääräinen poikkeama lasketaan seuraavalla kaavalla:

Missä n on käytettävissä olevien tietojen lukumäärä, x_Yllyttää Se edustaa kutakin tietoa ja x̄ on keskiarvo, joka määritetään lisäämällä kaikki tiedot ja jakamalla välillä n:

Keskimääräinen poikkeama antaa keskimäärin tietää, kuinka monta yksikköä data poikkeaa aritmeettisesta keskiarvosta, ja sillä on se etu, että sillä on samat yksiköt kuin tietojen kanssa, joiden kanssa se toimii.

Keskimmäinen poikkeamaesimerkki

Alueen tietojen mukaan merkittyjen tavoitteiden lukumäärä on:

40, 32, 35, 36, 37, 31, 37, 29, 39

Jos haluat löytää keskipitkän D -poikkeaman_M Näistä tiedoista on ensin laskettava x̄ aritmeettinen keskiarvo:

Ja nyt, kun X̄: n arvo on tiedossa, jatkamme keskimääräisen poikkeaman löytämistä_M-

= 2.99 ≈ 3 maalia

Siksi voidaan sanoa, että data siirtyy keskimäärin noin kolmeen keskimääräiseen tavoitteeseen, jotka ovat 35 tavoitetta, ja kuten huomautettiin, se on paljon tarkempi mitta kuin alue.

Voi palvella sinua: Hyperbola

Varianssi

Keskimääräinen poikkeama on paljon ohuempi variaatiomitta kuin alue, mutta kunkin datan ja keskiarvon välisten erojen absoluuttisen arvon kautta laskettuna se ei tarjoa suurempaa monipuolisuutta algebrallisesta näkökulmasta.

Siksi varianssi on edullinen, mikä vastaa kunkin datan kvadraattisen eron keskiarvoa keskiarvolla ja lasketaan kaavalla:

Tässä ilmaisussa S² tarkoittaa varianssia ja kuten aina x_Yllyttää edustaa kutakin tietoa, x̄ on keskiarvo ja n kokonaistiedot.

Kun työskentelet näytteen kanssa populaation sijasta, on suositeltavaa laskea varianssi näin:

Ero edellisen kaavan kanssa on, että nimittäjässä on n - 1 N: n sijasta. Se tapahtuu, että jakamalla n näytteen varianssi aliarvioi sen populaation varianssin, josta se uutettiin, mutta ei silloin, kun se on jaettu n -1: llä. Joissakin teksteissä, jotka lausekkeet näkyvät nimellä kvasi-variza.

Joka tapauksessa varianssille on ominaista olla aina positiivinen määrä, mutta on kvadraattisten erojen keskiarvo, on tärkeää huomata, että sillä ei ole samoja yksiköitä kuin data.

Esimerkki varianssista

Esimerkkien ja keskimääräisen poikkeaman tietojen varianssin laskemiseksi vastaavat arvot korvataan ja osoitettu summa. Tässä tapauksessa se on valittu jakamaan N-1: n välillä:

= 13.86

Keskihajonta

Varianssissa ei ole samaa yksikköä kuin tutkittavan muuttujan, esimerkiksi jos tiedot tulevat mittarina, varianssi johtaa neliömetreihin. Tai tavoitteiden esimerkissä, jotka olisivat maaliin, jolla ei ole mitään järkeä.

Voi palvella sinua: mitkä ovat vertauksen elementit? (Osat)

Siksi keskihajonta on määritelty, kutsutaan myös tyypillinen poikkeama, Kuten varianssin neliöjuuri:

S = √s²

Tällä tavalla tietojen variaatiomitta saadaan samoissa yksiköissä kuin nämä, ja mitä alhaisempi S: n arvo, sitä enemmän ryhmiteltyjä tietoja on keskiarvo.

Sekä varianssi että standardipoikkeama ovat variaatiomittauksia, jotka valitaan, kun aritmeettinen keskiarvo on keskeisen taipumuksen mitta, joka kuvaa parhaiten datan käyttäytymistä.

Ja se on, että keskihajonnalla on tärkeä ominaisuus, joka tunnetaan nimellä Chebyshevin lause: Ainakin 75% havainnoista on määritelty aikavälillä x̄ ± 2 s. Toisin sanoen 75% tiedoista on korkeintaan 2 s: n etäisyydellä keskimäärin.

Samoin vähintään 89% arvoista on 3 sekunnin etäisyydellä keskiarvosta, prosenttiosuus, jota voidaan laajentaa, edellyttäen, että monia tietoja on saatavana ja nämä seuraavat normaalia jakaumaa.

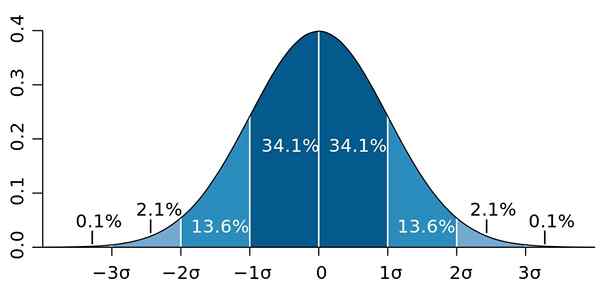
Kuva 2.- Jos tiedot seuraavat normaalia jakaumaa, 95.4 heistä on kaksi keskihajontaa keskiarvon molemmilla puolilla. Lähde: Wikimedia Commons.

Esimerkki keskihajonnasta

Edellisissä esimerkeissä esitettyjen tietojen keskihajonta on:

S = √s² = √13.86 = 3.7 ≈ 4 maalia