Jakelu F -ominaisuudet ja harjoitukset ratkaistu

Se Jakelu f o Fisher-Snedecor -jakauma on sitä, mitä käytetään kahden eri tai riippumattoman populaation varianssien vertaamiseen, joista kukin seuraa normaalia jakaumaa.

Jakelu, joka seuraa yhden normaalin populaation näytteiden varianssia, on Ji-neliöjakauma (Χ²) asteen n-1, jos jokaisessa sarjan näytteessä on n elementit.

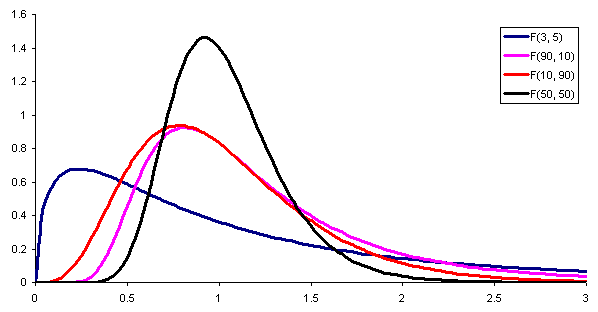
Kuvio 1. Tässä on jakauman F todennäköisyystiheys, joka on vastaavasti parametrien (tai vapausasteiden) yhdistelmiä vastaavasti. Lähde: Wikimedia Commons.

Kahden eri populaation varianssien vertaamiseksi on välttämätöntä määritellä a tilastollinen, toisin sanoen apuun satunnaismuuttuja, joka sallii selvittää, onko molemmilla populaatioilla sama varianssi vai ei.

Tämä apumuuttuja voi olla suoraan kunkin populaation näytteen varianssien osoitus, jolloin mainittu osamäärä on lähellä yksikköä, on todistettu, että molemmilla populaatioilla on samanlaisia ​​variansseja.

[TOC]

Tilastollinen F ja sen teoreettinen jakauma

Ronald Fisherin (1890 - 1962) ehdottama satunnaismuuttuja f tai tilastollinen f on sitä, jota käytetään useammin kahden populaation varianssien vertaamiseen ja se määritellään seuraavasti:

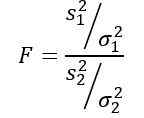
S -² Näytteen varianssi ja σ² Väestövarianssi. Kummankin väestöryhmän erottamiseksi käytetään vastaavasti tilauksia 1 ja 2.

On tiedossa, että Ji-neliöjakauma (N-1) vapausasteiden kanssa on se, joka seuraa jäljempänä määriteltyä apu- (tai tilastollista) muuttujaa:

X² = (N-1) s² / σ².

Siksi tilastot seuraavat seuraavan kaavan antamaa teoreettista jakaumaa:

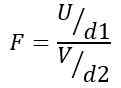
Olemus TAI Ji-neliöjakauma D1 = n1 - 1 väestönvapauden asteet 1 ja V Ji-neliöjakauma D2 = n2 - 1 väestönvapauden asteet 2.

Voi palvella sinua: Vector Algebra

Tällä tavalla määritelty suhde on uusi todennäköisyysjakauma, joka tunnetaan nimellä Jakelu f kanssa D1 Laskurin vapausasteet ja D2 nimittäjän vapausasteet.

Keskimääräinen, muoti ja jakeluvarianssi f

Puoli

Keskimääräinen jakauma F lasketaan seuraavasti:

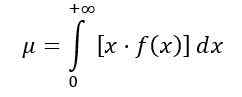
F (x) jakautumisen F todennäköisyystiheys, joka on esitetty kuvassa 1 useille parametrien yhdistelmille tai vapausasteille.

Voit kirjoittaa todennäköisyystiheyden F (x) γ -funktion riippuen (gammafunktio):

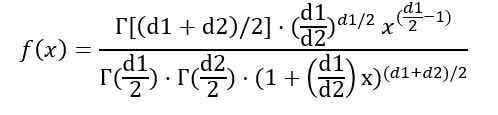
Kun aiemmin ilmoitettu integraali, päätellään, että jakauman F keskiarvo vapausasteilla (D1, D2) on: IS: IS:

μ = d2 / (d2 - 2) d2> 2: lla

Missä se osoittaa, että keskiarvo ei ole uteliaasti riippuvaisia ​​osoittajan vapausasteista D1.

Muoti

Toisaalta muoti riippuu D1: stä ja D2: sta, ja sen annetaan:

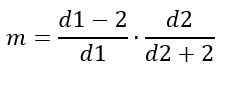
D1> 2.

Jakauman varianssi f

Varianssi σ² jakauman F lasketaan integraalista:

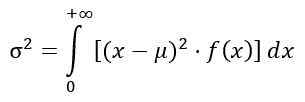
Saada:

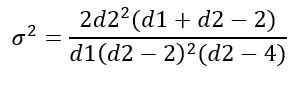
Jakelun hallinta f

Kuten muutkin jatkuvat todennäköisyysjakaumat, joihin liittyy monimutkaisia ​​toimintoja, jakelu F -hallinta tapahtuu taulukoiden tai ohjelmistojen avulla.

Jakelupöydät f

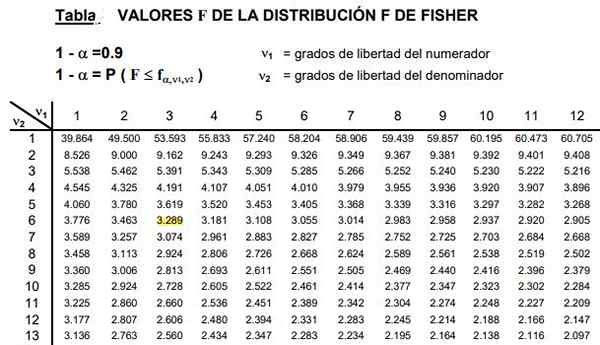Kuva 2. Osa F -jakelupöydästä on esitetty, jotka ovat yleensä erittäin laajoja, koska on olemassa laaja yhdistelmä mahdollisia vapausasteita D1 ja D2.

Taulukot sisältävät kaksi parametria tai jakautumisvapauden astetta f, sarake osoittaa numeraattorin vapauden asteen ja rivin nimittäjän vapausaste.

Voi palvella sinua: kolmion eriarvoisuus: esittely, esimerkit, ratkaisut harjoitukset

Kuvio 2 esittää osan F -jakautustaulukosta a: n tapauksessa merkitsevyystaso 10%, eli α = 0,1. F: n arvo korostetaan, kun D1 = 3 ja D2 = 6 kanssa luottamustaso 1- α = 0,9, joka on 90%.

Ohjelmisto jakeluun f

Jakelua hallitsevassa ohjelmistossa on suuri valikoima, laskentataulukoista Excel jopa erikoistuneet paketit, kuten Minitab, SPSS ja R - Jotta tunnetuimpia.

On huomattava, että geometria ja matematiikkaohjelmisto Geogebra Siinä on tilastollinen työkalu, joka sisältää pääjakaumat, mukaan lukien jakelu F. Kuvio 3 esittää jakauman F tapaukselle D1 = 3 ja D2 = 6 luottamustaso 90%.

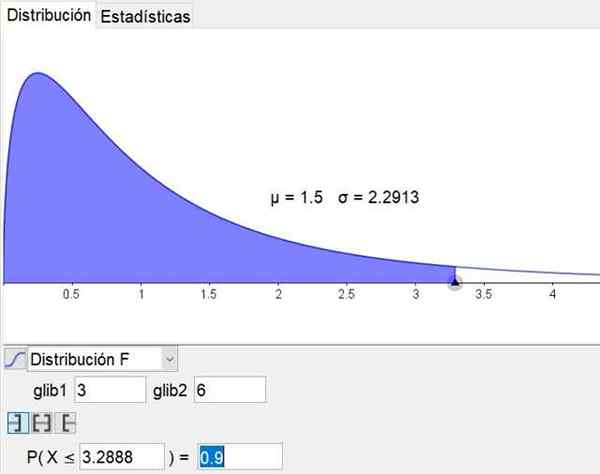Kuva 3. Jakauma F esitetään tapauksen D1 = 3 ja D2 = 6 90%: n luotettavuustasolla, joka saadaan geogebra -tilastollisen työkalun kautta. Lähde: Geogebra.org

Ratkaisut

Harjoitus 1

Harkitse kahta näytettä populaatioista, joilla on sama populaation varianssi. Jos näyte 1 on koko N1 = 5 ja näyte 2 on koko n2 = 10, määritä teoreettinen todennäköisyys, että sen vastaavien varianssien suhde on pienempi tai yhtä suuri kuin 2.

Ratkaisu

On muistettava, että tilastot F määritellään seuraavasti:

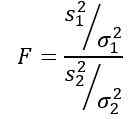
Mutta meille kerrotaan, että väestönvarianssit ovat samat, joten tätä harjoitusta varten sitä sovelletaan:

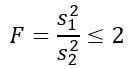
Koska haluat tietää teoreettisen todennäköisyyden, että tämä näytteen varianssien suhde on pienempi tai yhtä suuri kuin 2, meidän on tiedettävä jakautumisen F välillä 0 - 2, jotka voidaan saada taulukolla tai ohjelmistoilla. Tätä varten on otettava huomioon, että vaaditulla jakaumalla F on D1 = N1 - 1 = 5 - 1 = 4 ja D2 = N2 - 1 = 10 - 1 = 9, toisin sanoen jakauma F vapausasteissa (4, 9).

Se voi palvella sinua: Virusarja: Esimerkkejä ja harjoituksia

Käyttämällä tilastollista työkalua Geogebra Määritettiin, että tämä alue on 0.82, joten päätellään, että todennäköisyys, että näytteen varianssien suhde on pienempi tai yhtä suuri kuin 2 on 82%.

Harjoittele 2

On olemassa kaksi ohutta arkin valmistusprosessia. Paksuuden vaihtelun on oltava niin paljon kuin mahdollista. 21 näytettä jokaisesta prosessista otetaan. Prosessinäytteen standardipoikkeama on 1,96 mikronia, kun taas prosessin B keskihajonta on 2,13 mikronia. Millä prosessista on pienempi vaihtelu? Käytä 5%: n hylkäämistasoa.

Ratkaisu

Tiedot ovat seuraavat: sb = 2,13 nb = 21; SA = 1,96 NA = 21: llä. Tämä tarkoittaa, että sinun on työskenneltävä (20, 20) vapausasteen F: n kanssa F.

Nollahypoteesi tarkoittaa, että molempien prosessien populaation varianssi on identtinen, ts. Σa^2 / σb^2 = 1. Vaihtoehtoinen hypoteesi merkitsisi erilaisia ​​populaation variaatioita.

Sitten, identtisten populaation varianssien olettaen, tilasto f laskettuna seuraavasti: fc = (sb/sa)^2 on määritelty.

Koska hylkääminen on otettu a = 0,05, sitten α/2 = 0,025

Jakelu F (0.025; 20,20) = 0,406, kun taas F (0.975; 20,20) = 2,46.

Siksi nollahypoteesi on totta, jos F -laskettu on: 0,406≤fc≤2,46. Muuten nollahypoteesi hylätään.

Kuten fc = (2,13/1,96)^2 = 1,18 on päätelty, että FC -tilastot ovat nollahypoteesin hyväksymisalueella, jonka varmuus on 95%. Toisin sanoen 95%: n varmuudella molemmilla valmistusprosesseilla on sama populaation varianssi.

Viitteet

1. F Testi itsenäisyys. Toipunut: Saylordotorg.Github.Io.
2. Med -aalto. Terveystieteisiin sovelletut tilastot: Testi F. Toipunut: Medwave.Cl.
3. Todennäköisyydet ja tilastot. Jakelu f. Haettu: Todennäköisyys-.com.
4. Triola, m. 2012. Perustilastot. 11. päivä. Painos. Addison Wesley.
5. Yksinäinen. Jakelu f. Toipunut: Neuvonta.Cuautitlan2.Yksinäinen.MX.
6. Wikipedia. Jakelu f. Palautettu: on.Wikipedia.com