Vähiten neliöt

Mikä on vähimmäisruutujen menetelmä?

Menetelmä Vähiten neliöt Se on yksi tärkeimmistä sovelluksista toimintojen lähestymisessä. Ajatuksena on löytää käyrä sellainen. Toiminto voi olla viiva, neliömäinen käyrä, kuutio, jne.

Menetelmän tarkoituksena on minimoida ordinaattien erojen neliöiden summa (komponentti Y) valitun toiminnon tuottamien pisteiden ja tietojoukkoon kuuluvien pisteiden välillä.

Vähimmäismenetelmä

Ennen menetelmän antamista meidän on ensin oltava selkeä siitä, mitä "se on paremmin lähestymässä". Oletetaan, että viivaa etsitään y = b+mx, joka edustaa parhaiten joukko N ​​-pisteitä, nimittäin (x1, y1), (x2, y2)…, (xn, yn).

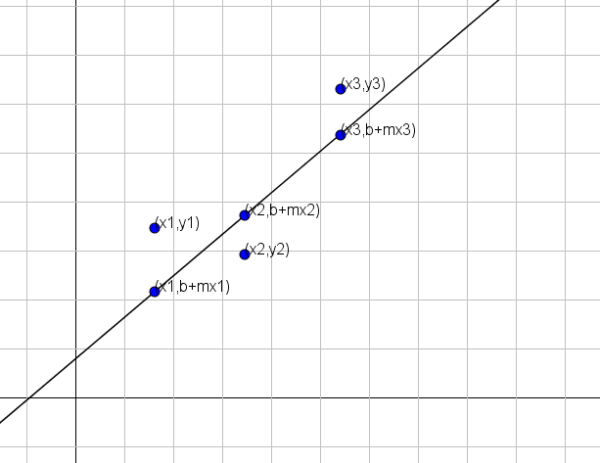
Kuten edellisessä kuvassa esitetään, jos muuttujat x ja y liittyivät linjalla y = b+mx, niin x = x1: lle vastaava Y: n arvo olisi B+MX1. Tämä arvo on kuitenkin erilainen kuin y: n todellinen arvo, joka on y = y1.

Muista, että tasossa kahden pisteen välinen etäisyys annetaan seuraavalla kaavalla:

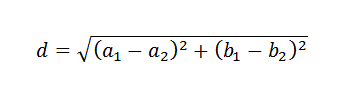
Tätä silmällä pitäen, jotta voidaan määrittää, kuinka linja Y = B+MX, joka parhaiten lähestyy annettuja tietoja, kuulostaa loogiselta käyttää kriteerinä linjan valinta, joka minimoi pisteiden välisten etäisyyksien summan Ja linja.

Koska pisteiden (x1, y1) ja (x1, b+mx1) välinen etäisyys on Y1- (B+MX1), ongelmamme pelkistetään lukujen M ja B löytämiseen siten, että seuraava summa on minimaalinen:

Voi palvella sinua: vihreä lause, esittely, sovellukset ja harjoitukset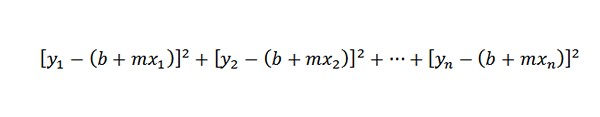

Tätä ehtoa täyttävä viiva tunnetaan "lähestymistapa vähimmäisruutujen linjaan pisteisiin (x1, y1), (x2, y2), ..., (xn, yn)".

Kun ongelma on saatu, on jäljellä vain menetelmä lähestymistavan löytämiseksi vähimmäisruutuilla. Jos pisteet (x1, y1), (x2, y2), ..., (xn, yn) ovat kaikki linjalla y = mx+b, meidän on oltava kolineaalinen ja:

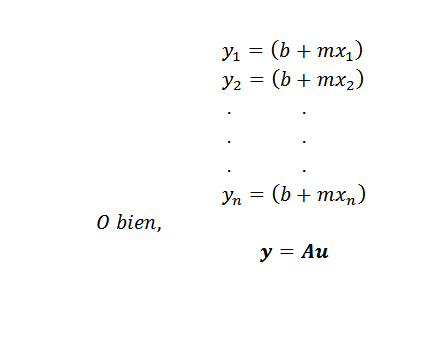
Tässä ilmaisussa:

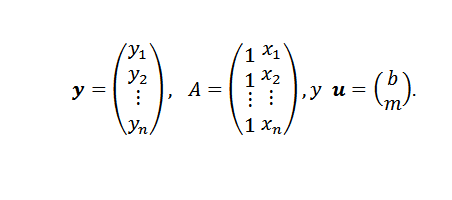
Lopuksi, jos pisteet eivät ole kolineaalisia, niin y-au = 0 ja ongelma voi johtaa vektorin löytämiseen tai siten, että euklidinen standardi on minimaalinen.

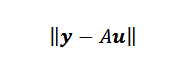
Minimoivan vektorin löytäminen tai ei niin vaikeaa kuin voisit ajatella. Koska A on NX2 ja U -matriisi on 2 × 1 -matriisi, meillä on, että auvektori on vektori R: ssäⁿ ja kuuluu A: n kuvaan, joka on R: n alatilaⁿ Ulottuvuudella enintään kaksi.

Oletetaan, että n = 3 osoittaa, mikä on menettely, jota on noudatettava. Jos n = 3, A -kuva on taso tai linja, joka kulkee alkuperän läpi.

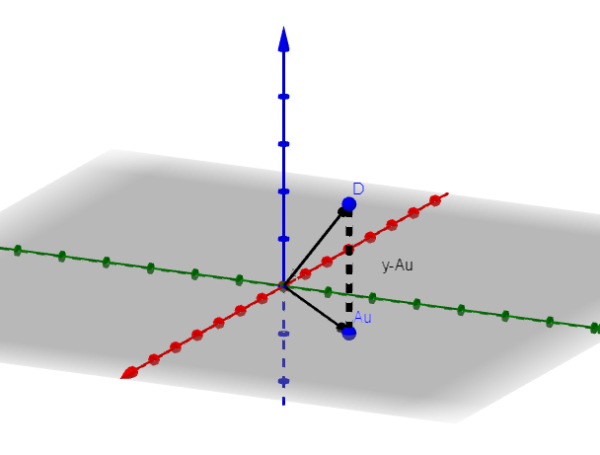
Olkoon V minimoi vektori. Kuvassa havaitsemme, että y-au on minimoitu, kun se on ortogonaalinen a. Eli jos V on minimoiva vektori, niin tapahtuu:

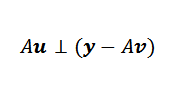
Sitten voimme ilmaista yllä mainitun:

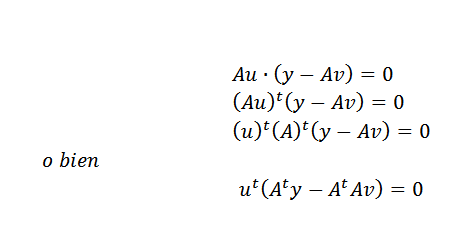
Tämä voi tapahtua vain, jos:

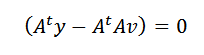
Lopuksi, puhdistaminen V, meidän on:

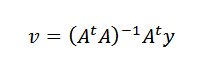
Tämä on mahdollista tehdä siitä lähtien^tA on käännettävä aina, kun N -pisteet, koska tiedot eivät ole kolineaalisia.

Nyt, jos etsimme linjaa, haluamme löytää vertauksen (jonka ilmaisu olisi muodoltaan y = a+bx+cx²) Että se oli parempi likiarvo datapisteille, menettely kuvataan alla.

Voi palvella sinua: kokonaiset numerot

Jos datapisteet olisivat siinä vertauksessa, sen olisi pitänyt:

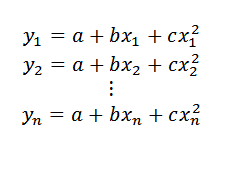
Sitten:

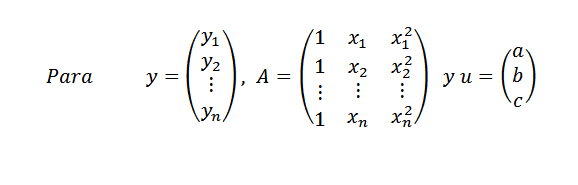
Samoin voimme kirjoittaa y = au. Jos kaikki kohdat eivät ole vertauksessa, meillä on, että y-au on erilainen nollasta millään vektorilla u ja ongelmamme on jälleen: etsi vektori U R3: sta siten, että sen normi || y-au || olla niin paljon kuin mahdollista.

Edellisen toimenpiteen toistaminen, pääsemme vektoriin haluttuun, on:

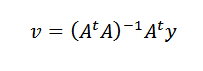
Ratkaisut

Harjoitus 1

Löydä pisteitä parhaiten sopiva linja (1,4), (-2,5), (3, -1) ja (4.1).

Ratkaisu

Meidän täytyy:

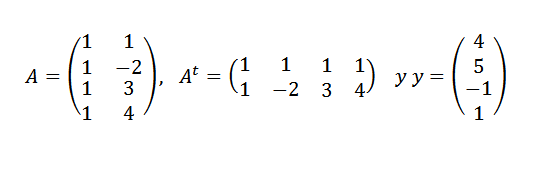
Sitten:

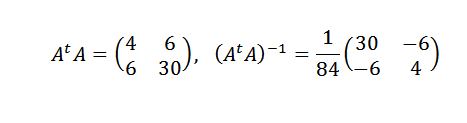
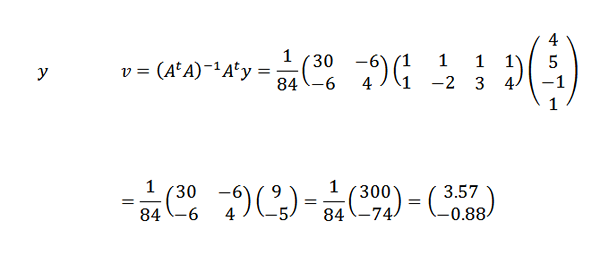
Siksi päättelemme, että pisteitä parhaiten sopivan linjan antaa:

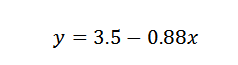
Harjoitus 2

Oletetaan, että esine pudotetaan 200 m: n korkeudesta. Seuraavat toimenpiteet toteutetaan: otetaan huomioon:

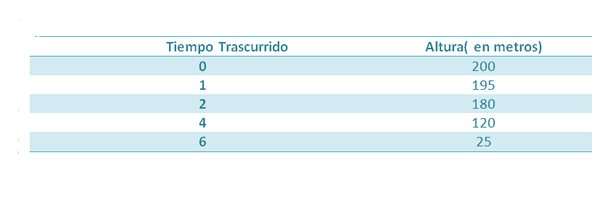
Tiedämme, että tämän esineen korkeus on kulunut ajan kuluttua:

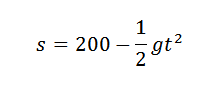
Jos haluamme saada G: n arvon, voimme etsiä vertausta, joka on parempi lähestymistapa taulukossa annettuihin viiteen pisteeseen, ja siten meillä olisi T -mukana oleva kertoimet² Se on kohtuullinen lähestymistapa (-1/2) g: lle, jos mittaukset ovat tarkkoja.

Meidän täytyy:

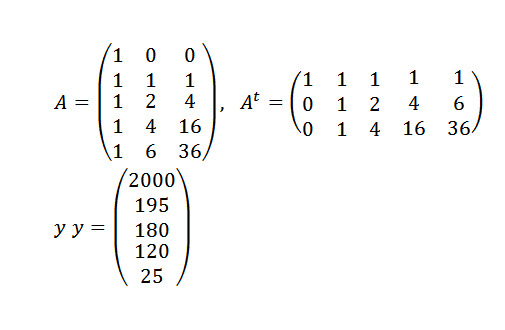
Ja sitten:

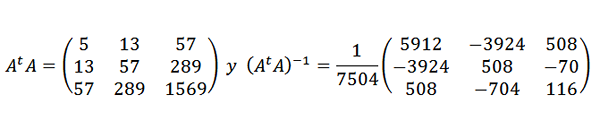
Joten datapisteitä säädetään seuraavalla neliömäisellä lausekkeella:

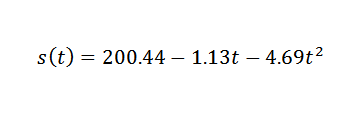
Joten sinun täytyy:

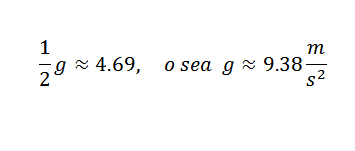
Tämä on arvo, joka on kohtuudella lähellä oikeaa, joka on g = 9,81 m/s². Tarkemman g g: n saamiseksi G: n on tarpeen aloittaa tarkempia havaintoja.

Mikä on vähimmäisnopeus menetelmä?

Luonnollisissa tai yhteiskuntatieteissä esiintyvissä ongelmissa on kätevää kirjoittaa eri muuttujien väliset suhteet jonkin matemaattisen ilmaisun kautta.

Voi palvella sinua: suhteellinen variaatio

Esimerkiksi, voimme liittyä talouteen kustannukset (c), tulot (i) ja voitot (U) yksinkertaisen kaavan kautta:

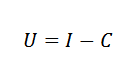
Fysiikassa voimme yhdistää painovoiman aiheuttaman kiihtyvyyden, aika, jolloin esine on pudonnut, ja esineen korkeus lain mukaan:

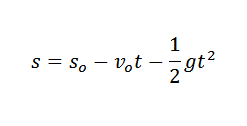
Edellisessä lausekkeessa S_jompikumpi Se on mainitun objektin ja V: n alkuperäinen korkeus_jompikumpi Onko alkuperäinen nopeus.

Näiden kaavojen löytäminen ei kuitenkaan ole yksinkertainen tehtävä; Se vastaa yleensä työssä olevaa ammattilaista työskennellä monien tietojen kanssa ja suorittaa toistuvasti useita kokeita (varmistaakseen, että saadut tulokset ovat vakioita) erilaisten tietojen välisten suhteiden löytämiseksi.

Yleinen tapa saavuttaa tämä on edustaa tasossa saatuja tietoja pisteinä ja etsiä jatkuvaa toimintoa, joka lähestyy näitä pisteitä optimaalisesti.

Yksi tapa löytää funktio, joka "parempia lähestymistapoja" annetut tiedot ovat neliön vähimmäismenetelmät.

Lisäksi, kuten näimme myös harjoituksessa, tämän menetelmän ansiosta voimme saavuttaa melko läheiset lähestymistavat fyysisiin vakioihin.