Vääntöhetki

Selitämme, mikä on vääntö, sen ominaispiirteet, kaavat, yksiköt, sovellukset ja ratkaisut harjoitukset

Mikä on vääntöaika?

Hän Vääntöhetki, vääntömomentti tai voimamomentti on voiman kyky aiheuttaa käännös. Etymologisesti sitä kutsutaan vääntömomentille englanninkielisen sanan johdannaisena Vääntömomentti, latinalaisesta Tontti (kierre).

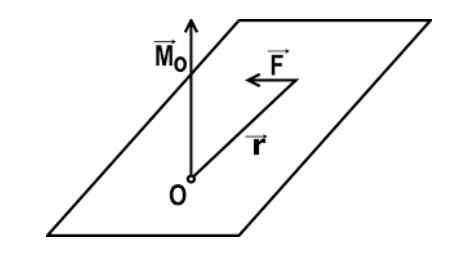
Vääntöaika (tiettyyn pisteeseen nähden) on fyysinen suuruus, joka johtuu vektorituotteen suorittamisesta sen pisteen sijaintivektoreiden välillä, jossa voimaa kohdistetaan ja kohdistetun voiman (ilmoitetussa järjestyksessä) (ilmoitetussa järjestyksessä). Tämä hetki riippuu kolmesta pääosasta.

Ensimmäinen näistä elementeistä on kohdistetun voiman suuruus, toinen on etäisyys sen pisteen välillä, jossa se kohdistuu, ja piste kehon suhteen pyörii (kutsutaan myös vipuvarsiin), ja kolmas elementti on kulman levitys sanottu voima.

Suurempi voima, suurempi käännös aiheutuu. Mitä sama pätee vipuvarsi: mitä suurempi etäisyys sen pisteen välillä, jossa voima ja piste kohdistetaan suhteessa käännöksen tuottamaan, sitä suurempi tämä tulee olemaan.

Loogisesti vääntöaika on erityisen kiinnostava rakentamiseen ja teollisuuteen, samoin kuin lukemattomissa kotisovelluksissa, esimerkiksi kun mutteri puristetaan englanninkielisellä avaimella.

Kaavat

Voiman vääntömomentin matemaattinen ilmentyminen pisteeseen nähden tai sen annetaan: m = r x f

Tässä lausekkeessa r on vektori, joka yhdistää O: n pisteen voiman levityksen pisteen P, ja F on kohdistetun voiman vektori.

Voi palvella sinua: sähköodynamiikka

Tällä hetkellä mitatut yksiköt ovat n ∙ m, jolla on heinäkuusta (J) vastaava ulottuvuus, ja niitä ei pidä sekoittaa, ja niitä ei pidä sekoittaa.

Siksi vääntömomentti moduuli ottaa seuraavan lausekkeen antaman arvon:

M = r ∙ f ∙ Sen α

Tässä ekspressiossa α on lujuusvektorin ja vektorin r tai vipuvarren kulma. Vääntöaikaa pidetään positiivisena, jos vartalo pyörii vastakkaiseen suuntaan kelloneulojen kanssa; Päinvastoin, se on negatiivinen, kun se kääntyy aikataulussa.

Yksiköt

Vääntöyksikkö on etäisyysyksikön voimayksikön tuote. Erityisesti kansainvälisessä yksikköjärjestelmässä käytetään Newton Metroa, jonka symboli on N • m.

Mittatasolla Newtonin metro voi vaikuttaa vastaavalta heinäkuusta; Heinäkuussa missään tapauksessa ei kuitenkaan käytetä hetkien ilmaisemiseen. Heinäkuu on yksikkö, jolla mitataan teoksia tai energioita, jotka käsitteellisestä näkökulmasta ovat hyvin erilaisia ​​kuin vääntöhetket.

Samoin vääntömomentti esittelee vektorihahmoa, joka on sekä työ- että mittakaavan energia.

Vääntömomentin ominaisuudet

Näkymästä seuraa, että pisteeseen kohdistuvan voiman vääntymismomentti edustaa voiman tai voimaryhmän kykyä muuttaa mainitun rungon pyörimistä akselin ympärillä, joka kulkee pisteen läpi kulkevan pisteen läpi.

Siksi vääntömomentti tuottaa kulmakiihtyvyyden kehossa ja on vektorihahmon suuruus (joten se on määritelty moduulista, suunnasta ja mielestä), joka on läsnä mekanismeissa, joille on altistettu vääntö tai taivutus.

Se voi palvella sinua: Vy canis majoris: löytö, ominaisuudet, rakenne, koulutus ja evoluutio

Vääntöaika on mitätön, jos lujuusvektorilla ja vektorilla r on samaan suuntaan, koska siinä tapauksessa SEN α: n arvo on mitätön.

Tuloksena oleva vääntömomentti

Ottaen huomioon tietty elin, jolla sarjajoukot käyttävät, jos sovelletut voimat toimivat samassa tasossa, vääntömomentti, joka johtuu kaikkien näiden voimien soveltamisesta; Se on vääntömomenttien summa kunkin voiman seurauksena. Siksi on toteutettu, että:

M_T = ∑ m = m₁ + M_{2 +} M₃ +..

Tietenkin on tarpeen ottaa huomioon vääntömomenttien merkkien kriteeri, kuten edellä selitettiin.

Sovellukset

Vääntömomentti on läsnä sovelluksissa yhtä päivittäin kuin puristamalla mutteri englantilaisella avaimella tai hanan tai oven avaaminen tai sulkeminen.

Sovelluksesi kuitenkin menee paljon pidemmälle; Vääntöaika löytyy myös koneiden akseleista tai niiden ponnistelujen tuloksista, joihin palkit altistetaan. Siksi sen sovelluksia teollisuudessa ja mekaniikassa ovat monia ja vaihtelevia.

Ratkaisut

Alla on pari harjoitusta edellä esitetyn ymmärryksen helpottamiseksi.

Harjoitus 1

Kun otetaan huomioon seuraava kuva, jossa pisteen O ja pisteiden A ja B väliset etäisyydet ovat vastaavasti 10 cm ja 20 cm:

a) Laske vääntömomentin arvo pisteeseen tai jos voimaa 20 N kohdistetaan pisteeseen A.

b) Laske, minkä pitäisi olla B: ssä sovelletun voiman arvo saavuttaa sama vääntöaika, joka saatiin edellisessä osassa.

Voi palvella sinua: Jatkuvuusyhtälö

Ratkaisu

Ensinnäkin tietojen tulisi kulkea.

r -_-Lla = 0,1 m

r -_{B -} = 0,2 m

a) Vääntömomentin laskemiseksi käytämme seuraavaa kaavaa:

M = r ∙ f ∙ Sen α = 0,1 ∙ 20 ∙ 1 = 2 n ∙ m

b) Pyydetyn voiman määrittämiseksi jatka samalla tavalla:

M = r ∙ f ∙ Sen α = 0,2 ∙ f ∙ 1 = 2 n ∙ m

Selvitys f saadaan, että:

F = 10 n

Harjoitus 2

Nainen suorittaa 20 N voiman englanninkielisen 30 cm: n pituuden lopussa. Jos voiman kulma avaimen avaimen kanssa on 30 °, mikä on mutterin kiertymisaika?

Ratkaisu

Seuraavaa kaavaa käytetään ja toimii:

M = r ∙ f ∙ Sen α = 0,3 ∙ 20 ∙ 0,5 = 3 n ∙ m