Tasainen pyöreä liike (m.C.TAI.) kaavat, ominaisuudet

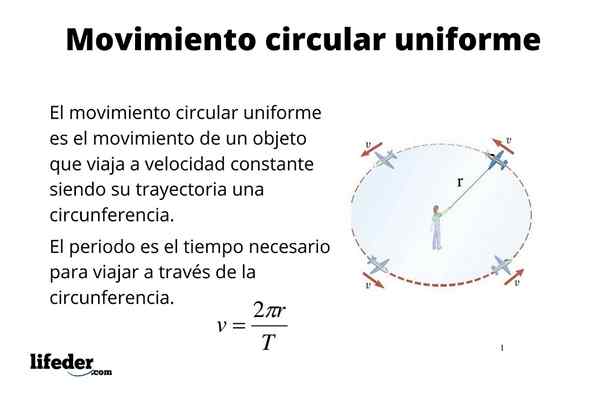
Hiukkasella on pyöreä liike yhtenäinen (M.C.TAI.) Kun sen etenemissuunta on kehä ja kulkee myös jatkuvasti. Lukuisilla esineillä, kuten esimerkiksi kone- ja moottoreilla, on tällainen liike, jonka joukossa tietokoneiden kiintolevyt, fenaterit, akselit ja monet muut asiat ovat enemmän.

Yhtenäinen pyöreä liike on myös hyvä lähestymistapa joidenkin taivaallisten kappaleiden, kuten maan, liikkeeseen. Maan kiertoradalla on todella elliptinen, kuten Keplerin lait huomauttavat. Kiertoradan epäkeskeisyys on kuitenkin pieni ja ensimmäisenä lähestymistapana sitä voidaan pitää ympyrä, mikä yksinkertaistaa joitain laskelmia, kuten maan nopeuden löytäminen, kun se liikkuu auringon ympäri.

Yhdenmukaisen pyöreän liikkeen kuvauksessa käytetään samoja parametreja kuin suoraviivaisessa liikkeessä, nimittäin: sijainti, siirtymä, aika, nopeus ja kiihtyvyys.

Kiihtyvyys? Kyllä, käytännössä yhtenäinen pyöreä liike kiihtyy, jopa sen nopeudella v olla vakiona. Tämä johtuu siitä, että nopeus v, Että se on vektori ja siksi se on lihavoitu, se muuttaa jatkuvasti suuntaansa, kun esine tai hiukkas pyörii. Kaikki muutokset v Sitä tuotetaan kiihtyvyydellä, joka, kuten se nähdään, on suunnattu kohti pyöreän radan keskustaa.

Yhtenäinen pyöreä liike on liike tasossa Xy, Siksi se on kahden ulottuvuuden liike. Hiukkasen pyyhkäisevän kulman θ läpi on kuitenkin mahdollista ilmaista mukavammin, mitattuna vaakasuoraan akseliin tai muuhun sopivaan referenssiakseliin.

Vaikka se olisi pidennetty esine, sen hiukkaset pyyhkäisevät aina saman kulman, vaikka niillä olisi erilaiset koordinaatit (X, y).

[TOC]

Yhtenäisen pyöreän liikkeen ominaisuudet

Voit tiivistää yhtenäisen pyöreän liikkeen ominaisuudet seuraavasti:

-Etenemissuunta on kehä, joten se on liikettä lentokoneessa.

-Nopeus v Se on vakio, mutta nopeus v Ei, koska se muuttaa jatkuvasti suuntaa ja merkitystä matkapuhelimen vuoron mukauttamiseksi.

-Nopeusvektori v Se on aina tangentiaalinen kehälle ja kohtisuorassa säteittäiseen suuntaan nähden.

-Kulmanopeus ω on vakio.

-Huolimatta yhtenäisestä, on kiihtyvyys selittää nämä muutokset nopeuden suunnassa. Tämä kiihtyvyys on keskikiihtyvyys.

-Centripetaalinen kiihtyvyys ja nopeus ovat kohtisuorassa toisiinsa nähden.

-Se on määräajoin tai toistuva liike, joten hänelle määritetään suuruusjakso ja taajuus.

Yhtenäiset ympyrämuotoiset kaavat

Tässä kaaviossa on p -hiukkasten pyöritys v piirretty.

Voi palvella sinua: Maan magneettikenttä: alkuperä, ominaisuudet, toiminto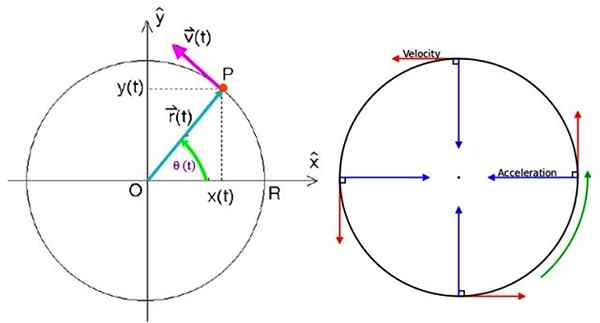 Yhtenäiset ympyränmuotoiset parametrit. Lähde: f. Zapata/Wikimedia Commons.

Asetusvektorin määrittämiseksi se on välttämätöntä.

Asentovektori

Se on merkitty nimellä r (t) ja se on suunnattu alkuperästä pisteeseen P, jossa hiukkas sijaitsee. Hetkellä t, Cartesian koordinaateissa, se on kirjoitettu seuraavasti:

r - (t) = x (t) Yllyttää + ja T) J -

Missä Yllyttää ja J - Ne ovat kohtisuora yksikkövektorit suunnissa x ja ja vastaavasti. Kaaviosta havaitaan, että vektorimoduuli r - (t) aina okei R -, Ympäryssäde. Jos θ on kulma, joka muodostaa r - Vaaka -akselilla myös sijainti on yhtä suuri kuin:

r - (t) = [RCOS θ(t)] Yllyttää +[Rsen θ(t)] J -

Muodostuu kulma r - (T) Vaaka -akselilla se on keskuskulma ja sen arvo on:

θ = s/r

Missä S on kehäkaari kulki ja r radio. Mainittu kulma θ Se on aikatoiminto, joten voit kirjoittaa θ = θ (T), puhelu kulma.

Koska nopeus on vakio, hiukkas kuvaa yhtä suuria kulmia yhtäläisinä aikoina ja analogisesti tasaisen välittömän liikkeen kanssa, se on kirjoitettu:

θ = θ (t) = θ_jompikumpi + ωt

Tässä θ_jompikumpi Se on radiaaneissa mitattu alkukulma referenssiakseliin, se voi olla 0 tai mikä tahansa arvo ja ω on kulmanopeus.

Kulmanopeus ja lineaarinen nopeus

Kulmanopeus on ensimmäinen johdettu kulma -asennosta ja se on merkitty ω. Sen arvo on vakio yhtenäisen pyöreän liikkeen kannalta, koska yhtäläiset kulmat ovat aidat yhtäläisinä aikoina. Toisin sanoen:

Kulmanopeus on Radians/S: n yksiköissä. Lineaarinen nopeus laskee puolestaan:

Lineaarinen nopeus on lineaarisen nopeuden moduuli tai suuruus, joka muuttuu hiukkasten kääntyessä sen etenemissuunnan jälkeen. Nopeussuunta on siten ympärysmiilleen tangentiaalinen osoite.

Yhdenmukaisen pyöreän liikkeen lineaarisen nopeuden yksiköt ovat samat kuin lineaarisissa liikkeissä: m/s (kansainvälisessä järjestelmässä Si), KM/H, CM/S ja muut.

Centripetaalinen kiihtyvyys

Seuraavassa kuvassa on hiukkas, joka liikkuu kehän aikataulussa vakiona nopeudella. Tämä tarkoittaa, että nopeusvektorilla on aina sama moduuli, mutta se muuttaa suuntaa ympärysmiilleen.

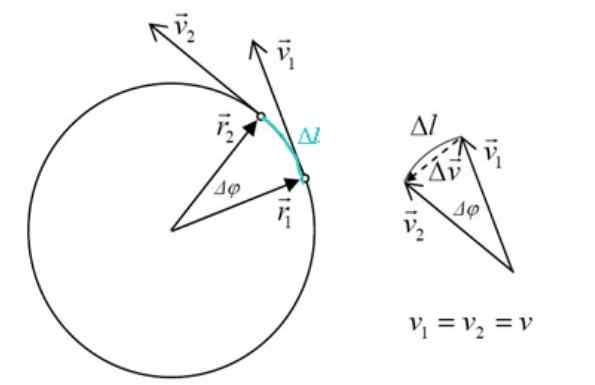Nopeus ja kiihtyvyys yhtenäisessä pyöreässä liikkeessä. Lähde: f. Zapata.

Nopeuden tulosten muutos kiihtyvyyteen, mikä määritelmän mukaan:

Voi palvella sinua: 31 fysiikan voimantyyppiä ja niiden ominaisuuksia

Yllä olevassa kuvassa on vähennys vektorien keskuudessa v₂ ja v₁, jonka tulos on δv, vektori verrannollisesti kiihtyvyyteen. Kuten näette, viittaa aina kehän keskustaan, ja siksi sitä kutsutaan centripetaaliksi kiihtyvyyksi.

Kolmio muodostettu v₂, v₁ ja Δv Se on samanlainen kuin sivut kolmio r -₂, r -₁ ja Δlens, On Δpuolella keskuskulma. Suuruudet r -₂ ja r -₁ Ne ovat samoja, joten:

r -₂ = r₁ = r

Sitten molemmista kolmioista ovat nämä suhteet kulmaan:

Δφ = Δr / r; Δφ = ΔV / V

Lihavoitu ei ole välttämätöntä, koska kulman mitta riippuu näiden vektorien suuruuksista. Yllä olevien lausekkeiden tasoittaminen seuraa, että:

 Niin:

Jakaminen molemmille puolille Δt, kiihtyvyyden suuruuden saamiseksi:

Mutta ΔR / ΔT on nopeuden suuruus, nimeltään v, siksi:

Lopuksi centripetaalinen kiihtyvyys on:

Ajanjakso ja taajuus

Koska pyöreä liike on toistuva, ajanjakso on määritelty T Sama kuin aika, joka matkapuhelin on kääntynyt täydellisesti. Koska säteen R säteen pituus on 2πr, kulma pyyhkäisi radianeissa kääntyessä täydellisenä on 2π radiaania ja vie aikaa t, kulmanopeus on:

Ω = 2π / t

T = 2π / Ω

Yhtenäisen pyöreän liikkeen ajanjakso mitataan sekunneissa kansainvälisessä järjestelmässä.

Puolestaan, taajuus F Se on käännösten lukumäärä aikayksikköä kohti ja on ajanjakson vastavuoroinen tai käänteinen:

F = n /t = 1 /t

Kansainvälisen järjestelmän taajuusyksikkö on S^-1.

Yhtenäiset pyöreät liikkeen esimerkit

Monet esineet pyörivät tuottamaan erilaisia ​​vaikutuksia: pyörät, levyt ja turbiinit. Kun käyttö nopeus on saavutettu, kierto suoritetaan yleensä vakiona nopeudella. Pyöreä liike on niin yleinen jokapäiväisessä elämässä, että et melkein koskaan ajattele sitä, joten tässä on joitain läheisiä esimerkkejä, jotka kuvaavat sitä erittäin hyvin:

Maan liike

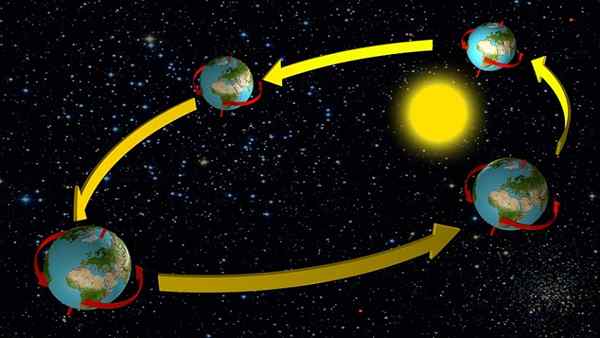
Maa- ja muut aurinkokunnan planeetat liikkuvat pienen epäkeskeisyyden elliptisissä suuntauksissa, paitsi elohopea, mikä tarkoittaa, että ensimmäisessä lähestymistavassa voidaan olettaa, että sen liike on tasainen ympyrä.

Tällä on hyvä käsitys käännöksen nopeudesta auringon ympärillä, koska maan tapauksessa tiedetään liikkumiskausi: yksi vuosi tai 365 päivää.

Hiukkaset albumin reunalla

Hiukkaset, jotka pyörivät muinaisen Toadiscosin tai tuulettimen viipalan reunalla, seuraavat yhtenäistä pyöreää liikettä, kun laite saavuttaa lisääntymisnopeutensa.

Voi palvella sinua: Dirac Jordan Atomic -malli: Ominaisuudet ja postulaatit

Hubble -avaruusteleskooppi

Hubble -avaruusteleskooppi pyörii maan ympäri noin 7550 m/s.

Sentrifugaattorit

Pesukoneet suorittavat sentrifugoidun prosessin vaatteiden puristamiseksi, joka koostuu suurnopeuden astiarummun pyörimisestä. Kuivaimet kääntyvät myös tietyn ajanjakson yhtenäisen pyöreän liikkeen kanssa.

Sentrifugointia käytetään myös laboratorioissa esimerkiksi yhdisteiden erottamiseen ja siten erottamiseen sen ainesosat tiheyserojen perusteella. Aina kun sentrifugoinnista puhuu, on pyöreä liike, joka on tasainen, ainakin jonkin aikaa.

Puutarhasuihkut

Monet puutarhasovellukset kääntyvät jatkuvasti maan vedestä parissa.

Urheilu

Esimerkiksi vasaran lanseerauksessa, joka on olympiakisoja, urheilija kääntää metallipallon, jossa on teräskaapeli, joka on kiinnitetty kahvaan. Tavoitteena on lähettää pallo mahdollisimman pitkälle, mutta jättämättä tietystä alueesta.

Liikuntaa

Hiukkas liikkuu 2 m: n sädeympyrässä vakiona nopeudella v = 8 m/s, vastakkaiseen suuntaan kuin kello. Alun perin hiukkas oli r - = +2 J - m. Laskea:

a) kulmanopeus ω

b) sen kulma -asema θ (t)

c) liikevaihto

d) Centripetaalinen kiihtyvyys.

e) Hiukkasten sijainti t = π/4 s

Liittää jhk

Kaavasta v = rω se seuraa, että:

Ω = v/r = (8 m/s)/2M = 4Rad ∙ S^-1

Ratkaisu b

Positiivisen X -akselin referenssiakselina hiukkaset ovat aluksi 90º = π/2 radiaania mainitun akselin suhteen, koska lausunnossa sanotaan, että alkuperäinen sijainti on +2 J - M, toisin sanoen hiukkas on y = 2m, kun liike alkaa seurata.

θ = θ (t) = θ_jompikumpi + ωt = π/2 + 4T

Liuos C

T = 2π / ω = 2π / 4 s = 0.5 π s

Liuos D

A = V² / R = (8 m/ s)² / 2 m = 32 m/ s²

Ratkaisu E

θ (t) = π/2 + 4T → θ (π/4) = π/2 + 4 ∙ (π/4) = 3π/2 radiaanit

Tämä tarkoittaa, että tuon ajan kuluttua hiukkas on asemassa y = -2m J -. Se on järkevää, koska t = π/4 s on puolet ajanjaksosta, joten hiukkaset kiertävät 180º kulmaa anti -horary -merkityksessä sen alkuperäisen aseman jälkeen ja sen on oltava oikeassa vastakkaisessa asennossa.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 1. Kinematiikka. Toimittanut Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
5. Zapata, f. Pyöreä liike. Toipunut: Francesphysics.Blogin.com.