Yhtenäiset suorakulmaiset liikkumisominaisuudet, kaavat, harjoitukset

Hän yhtenäinen linjaliike tai vakiona nopeudella on yksi, jossa hiukkas liikkuu suoraa linjaa pitkin ja vakiona nopeudella. Tällä tavoin matkapuhelin kulkee yhtä suuret etäisyydet yhtäläisinä aikoina. Esimerkiksi, jos se kulkee 1 sekunnissa 2 metriä, 2 sekunnin kuluttua on 4 metriä ja niin edelleen.

Tarkat kuvauksen liikkeestä, olipa sitten yhdenmukainen suorakulmainen tai muu, on välttämätöntä luoda vertailupiste, jota kutsutaan myös alkuperä, jonka mobiili muuttaa sijaintia.

Kuvio 1. Autolla, joka liikkuu suorakulmaista tietä pitkin vakiona nopeudella, on tasainen suorakulmainen liike. Lähde: Pixabay.

Jos liike kulkee kokonaan suoraa linjaa pitkin, se on myös kiinnostunut tietämään, missä mielessä matkapuhelin matkustaa.

Vaakaviivalla on mahdollista, että matkapuhelin menee oikealle tai vasemmalle. Kahden tilanteen välinen ero on merkinnöillä, seuraavana seuraava: oikealla puolella (+) ja vasemmalle merkki (-).

Kun nopeus on vakio, matkapuhelin ei muuta sen suuntaa tai merkitystä, ja myös sen nopeuden suuruus pysyy muuttumattomana.

[TOC]

Ominaisuudet

Yhtenäisen suorastettua liikkeen (MRU) pääominaisuudet ovat seuraavat:

-Liike kulkee aina suoraa linjaa pitkin.

-Matkapuhelin, jolla on MRU.

-Nopeus pysyy muuttumattomana sekä suuruudessa että suunnassa.

-MRU: sta puuttuu kiihtyvyys (nopeudenmuutoksia ei tapahdu).

-Koska nopeus v pysyy vakiona ajan myötä t, Sen suuruuskaavio ajan funktiona on suora. Kuvan 2 esimerkissä viiva on vihreä ja nopeuden arvo luetaan pystysuoralla akselilla, noin +0.68 m/s.

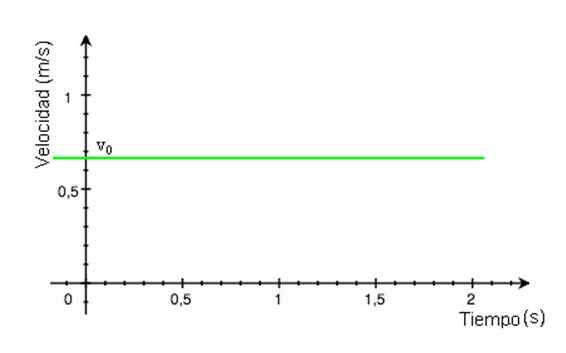Kuva 2. Nopeuskaavio MRU: sta riippuen. Lähde: Wikimedia Commons.

-X -aseman kuvaaja ajan suhteen on suora viiva, jonka kaltevuus vastaa liikkuvan nopeuden. Jos x vs t -kuvaajaviiva on vaakasuora, matkapuhelin on levossa, jos kaltevuus on positiivinen (kuvan 3 kaavio), nopeus on myös.

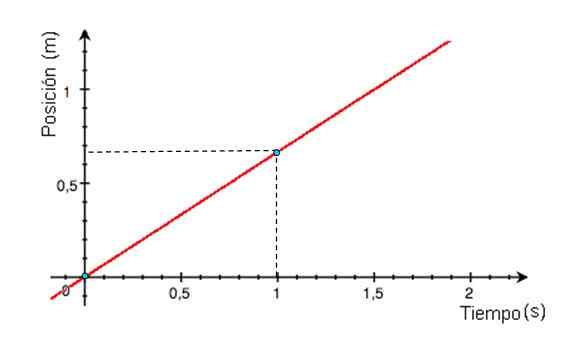Kuva 3. Kaavio sijainnista ajan funktiona matkapuhelimelle, jolla on MRU, joka poistui alkuperästä. Lähde: Wikimedia Commons.

Graafista V vs. kulunut etäisyys. t

Tunne matkapuhelimen kuljettama etäisyys, kun kuvaaja on saatavana V. t on hyvin yksinkertainen. Kuljettu etäisyys vastaa linjan alla olevaa aluetta ja sisältyy haluttuun aikaväliin.

Se voi palvella sinua: keskimääräinen kiihtyvyys: miten se lasketaan ja ratkaistaan

Oletetaan.5 ja 1.5 sekuntia.

Tämä alue on kuvassa 4 varjostettu suorakulmio. Se lasketaan etsimällä tulos suorakulmion pohjan kertomisesta sen korkeudella, jonka arvot luetaan graafisesta.

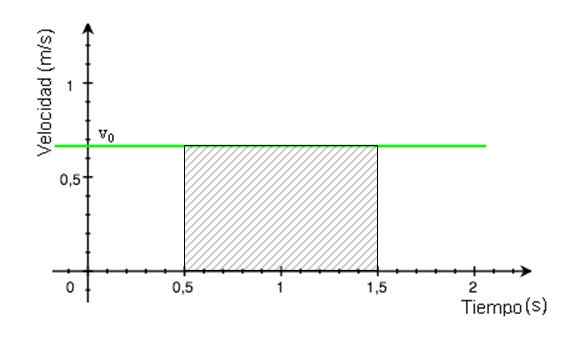Kuva 4. Raidallinen alue vastaa kulkettua etäisyyttä. Lähde: Modifioitu Wikimedia Commons.

Ajattu etäisyys = (1.viisikymmentä.5) x 0.68 m = 0.68 m

Etäisyys on aina positiivinen määrä riippumatta siitä, menetkö oikealle vai vasemmalle.

Kaavat ja yhtälöt

MRU: ssa keskimääräinen nopeus ja hetkellinen nopeus ovat aina samat ja koska sen arvo on kaavion X vs. vastaava kaltevuus, vastaavat yhtälöt ajan riippuen ovat seuraavat:

-Sijainti ajasta riippuen: x (t) = x_jompikumpi + VT

x_jompikumpi Se edustaa matkapuhelimen alkuperäistä sijaintia, useissa tapauksissa se vastaa vertailujärjestelmän alkuperää, mutta se ei aina ole tällainen. Tämä yhtälö tunnetaan myös nimellä Reittiyhtälö.

-Nopeus ajasta riippuen: v (t) = vakio

Kun v = 0 tarkoittaa, että matkapuhelin on lepo. Lepo on erityinen liiketapaus.

-Kiihtyvyys ajan funktiona: A (t) = 0

Yhtenäisessä suorakulmiossa ei tapahdu nopeusmuutoksia, joten kiihtyvyys on nolla.

Ratkaisut

Harjoituksen ratkaisemisessa on varmistettava, että tilanne vastaa käytettävää mallia. Erityisesti ennen MRU -yhtälöiden käyttöä on tarpeen varmistaa, että niitä voidaan soveltaa.

Seuraavat ratkaisut ovat kaksi mobiili -ongelmaa.

Liikunta ratkaistiin 1

Kaksi urheilijaa lähestyy toisiaan jatkuvalla nopeudella 4.50 m/s ja 3.5 m/s, vastaavasti erotettuna alun perin 100 metrin etäisyyden, kuten kuvassa on osoitettu.

Jos kukin ylläpitää jatkuvaa nopeuttaan, etsi: a) kuinka kauan tapaaminen kestää? b) mikä on kunkin sijainti tuolloin?

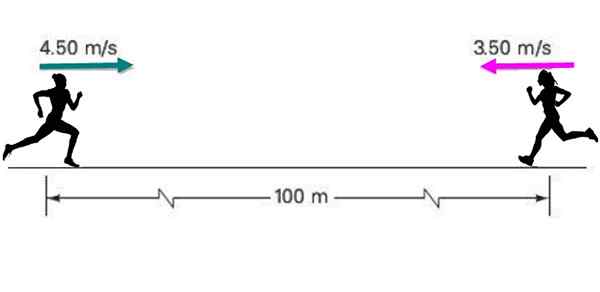Kuva 5. Kaksi juoksijaa siirtyy toisiinsa vakiona. Lähde: Itse tehty.

Ratkaisu

Ensimmäinen on osoittaa koordinaattijärjestelmän alkuperä, joka toimii viitteenä. Valinta riippuu mieluummin, että ongelman ratkaiseva henkilö on.

Voi palvella sinua: mikä on tilavuuslaatta? (Esimerkkejä)

Se valitaan yleensä x = 0 heti matkapuhelimien lähtökohdassa, se voi olla vasemman tai oikean juoksija, se voidaan jopa valita molempien keskellä.

a) Aiomme valita x = 0 vasemman tai juoksijan 1 juoksijalla, joten tämän alkupaikka on x₀₁ = 0 ja juoksijalle 2 on x₀₂ = 100 m. Välittäjä 1 siirtyy vasemmalta oikealle nopeudella v₁ = 4.50 m/ kun Runner 2 tekee sen oikealta vasemmalle nopeudella -3.50 m/s.

Liikeyhtälö ensimmäiselle välittäjälle

x₁ = x₀₁ + v₁t₁ = 4.50T₁

Liikkeen yhtälö toiselle välittäjälle

x₂ = x₀₂ + v₂t₂ = 100 -3.50T₂

Aika on sama molemmille t₁ = t₂ = t , Kun molempien sijainti on sama, siksi x₁ = x₂. Yhtä suuri:

4.50T = 100 -3.50T

Se on ajan ensimmäisen asteen yhtälö, jonka ratkaisu on t = 12.5 s.

b) Molemmat juoksijat ovat samassa asennossa, joten se korvaa edellisessä osassa saadun ajan missä tahansa sijaintiyhtälössä. Esimerkiksi voimme käyttää juoksijaa 1:

x₁ = 4.50T₁ = 56.25 m

Sama tulos saadaan korvaamalla t = 12.5 s juoksijan asennossa yhtälö 2.

-Liikunta ratkaistiin 2

Jänpe haastaa kilpikonnan juoksemaan 2 etäisyyden.4 km ja ollakseni rehellinen, se tarjoaa puoli tuntia etua. Pelissä kilpikonna etenee järkeessä 0.25 m/s, joka on maksimi, joka voi käyttää. 30 minuutin kuluttua jänis kulkee 2 m/s ja saavuttaa kilpikonnan nopeasti.

Kun jatkat vielä 15 minuuttia, ajattele, että hänellä on aikaa nukkua ja voittaa silti kilpailu, mutta nukahtaa 111 minuuttia. Herääessään hän juoksee kaikin voimin, mutta kilpikonna oli jo ylittämässä maalia. Löytö:

a) Mitä etuja kilpikonna voittaa?

b) ajan hetki, jolloin jänis edistää kilpikonnia

c) hetki, jolloin kilpikonna etenee jänikseen.

Ratkaisu)

Kilpailu alkaa t = 0. Kilpikonnan sijainti: x_T = 0.25T

Jänisen liikkeellä on seuraavat osat:

Voi palvella sinua: aurinkojärjestelmä: planeetat, ominaisuudet, alkuperä, evoluutio

-Lepää kilpailun antaman etua varten: 0 < t < 30 minutos:

-Kilpailu saavuttaa kilpikonna ja jatkaa juoksemista vähän sen jälkeen, kun se on ohittanut; Kaiken kaikkiaan ne ovat 15 minuuttia liikettä.

-Nuku 111 minuuttia (lepo)

-Herää liian myöhään (sprintti lopullinen)

2.4 km = 2400 m

Kilpailun kesto oli: T = 2400 m/ 0.25 m/s = 9600 s = 160 min. Tällä hetkellä vähennämme 111 minuutin päässä nukkumasta ja 30 edusta, joka on 19 minuuttia (1140 sekuntia). Se tarkoittaa, että hän juoksi 15 minuuttia ennen nukkumista ja 4 minuuttia sprintin heräämisen jälkeen.

Tällä hetkellä jänis kattoi seuraavan etäisyyden:

d -d_Lens = 2 m/s . (viisitoista . 60 s) + 2 m/s (4. 60 s) = 1800 m + 480 m = 2280 m.

Koska kokonaisetäisyys oli 2400 metriä, vähentäen molemmat arvot, käy ilmi, että jänis puuttui 120 metriä tavoitteen saavuttamiseksi.

Ratkaisu b)

Jänin sijainti ennen nukahtamista on x_Lens = 2 (t - 1800), Kun otetaan huomioon 30 minuutin viive = 1800 sekuntia. Yhtä suuri kuin x_T ja x_Lens Löydämme aika, jonka he ovat:

2 (T - 1800) = 0 -.25T

2T -0.25 t = 3600

T = 2057.14 s = 34.29 min

Liuos c)

Kilpikonnan edistäessä jäniksen edistäessä se nukkuu 1800 metrin päässä pelistä:

1800 = 0.25T

T = 7200 s = 120 min

Sovellukset

MRU on yksinkertaisin liike, joka voidaan kuvitella, ja siksi se on ensimmäinen tutkittu elokuvassa, mutta monia monimutkaisia ​​liikkeitä voidaan kuvata tämän ja muiden yksinkertaisten liikkeiden yhdistelmänä.

Jos henkilö poistuu talostaan ​​ja johtaa, kunnes hän saavuttaa pitkän suorakulmaisen moottoritien, jonka läpi hän matkustaa samalla nopeudella pitkään, hänen MRU: n liikkeen.

Tietysti henkilön on otettava muutama kierros ennen moottoritieltä saapumista ja poistumista, mutta tämän liikemallin käytön kautta matkan kesto voidaan arvioida tietäen lähtökohdan ja saapumispisteen likimääräisen etäisyyden.

Luonnossa valolla on tasainen suorakulmainen liike, jonka nopeus on 300.000 km/s. Äänen liikkuminen ilmassa voidaan myös olettaa tasaisen suorakulmion nopeudella 340 m/s lukuisissa sovelluksissa.

Analysoidessa muita ongelmia, esimerkiksi kuljettajien kuljettajien kuljettajien liikkumista, MRU -lähestymistapaa voidaan käyttää myös käsitys siitä, mitä kuljettajan sisällä tapahtuu.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.40-45.
2. Figueroa, D. Fyysinen sarja tiedettä ja tekniikkaa. Osa 3. Painos. Kinematiikka. 69-85.
3. Giancoli, D.  Fysiikka: sovellusten periaatteet. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Käsitteellinen fysiikka. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen. 15-19.
6. Wilson, J. 2011. Fysiikka 10. Pearson -koulutus. 116-119.