Suhteellinen liikkuminen ulottuvuudessa, kahdessa ulottuvuudessa, harjoituksissa

Hän suhteellinen liike hiukkasen tai objektin ollessa havaittu tiettyyn vertailupisteeseen, jonka tarkkailija on valinnut, jotka voivat olla kiinteitä tai liikkua. Nopeus viittaa aina joihinkin koordinaattijärjestelmiin, joita käytetään sen kuvaamiseen.

Esimerkiksi liikkuvaan auton co -piLot ja se, joka matkustaa mukavasti nukkumaan istuimellaan.

Kuvio 1. Lentokoneet ylläpitävät tietyn suhteellisen nopeuden niiden välillä harjoitellen akrobatiaa. Lähde: Pixabay.

Sitten liike on aina suhteellista, mutta tapahtuu, että koordinaatti- tai vertailujärjestelmä valitaan yleensä, sillä sen alkuperä maassa tai maassa, paikka, jota pidetään paikallaan. Tällä tavoin huolenaihe keskittyy tutkitun kohteen liikkeen kuvaamiseen.

Onko mahdollista kuvata nukkuvan kodinopeuden nopeutta toisessa autossa kulkevan matkustajan suhteen? Vastaus on kyllä. On vapaus valita arvo (x_jompikumpi, ja_jompikumpi, z -z_jompikumpi): Referenssijärjestelmän alkuperä. Valinta on mielivaltainen ja riippuu tarkkailijan mieltymyksestä sekä ongelman ratkaisemisesta tarjoamasta helpotuksesta.

[TOC]

Suhteellinen liike ulottuvuudessa

Kun liike kulkee suoraa linjaa pitkin, matkapuhelimilla on nopeudet samaan suuntaan tai vastakkaiseen suuntaan, molemmat havaitsija seisoo maassa (t) (t). Liikkuu tarkkailija matkapuhelimien suhteen? Kyllä, samalla nopeudella, mutta vastakkaiseen suuntaan.

Kuinka mobiili liikkuu suhteessa toiseen? Selvitä, että nopeudet lisätään vektoriin.

Se voi palvella sinua: Pluto (Dwarf Planet)

-Ratkaistu esimerkki 1

Ilmoita auton 1 suhteellisen nopeuden osassa esitetyn kuvan suhteen auto 2: n suhteen kussakin tilanteessa.

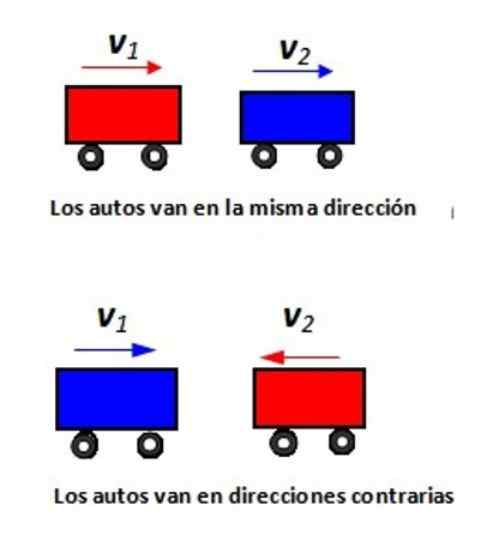Kuva 2. Kaksi autoa kulkee suoraviivaisella tiellä: a) samaan suuntaan ja b) vastakkaisiin suuntiin.

Ratkaisu

Määritämme positiivisen merkin oikealle ja negatiivinen merkki vasemmalla. Jos matkapuhelin menee oikealle nopeudella 80 km/h, tämän matkapuhelimen matkustaja näkee tarkkailijan kentällä siirtymässä - 80 km/h.

Oletetaan, että kaikki tapahtuu X -akselia pitkin. Seuraavassa kuvassa punainen auto liikkuu nopeudella +100 km/h (nähty T: stä) ja valmistautuu ohittamaan sinisen auton, joka kulkee nopeudella +80 km/h (nähty myös T: stä). Millä nopeudella näet matkustajan lähestyvän punaisen auton sinisen auton?

Tarrat ovat: v _1/2 Automaattinen 1 nopeus suhteessa 2, v_1/t Auton nopeus suhteessa t, v_T/2 Taulukon nopeus suhteessa 2. Lisäämällä vektorisesti:

v_1/2 = v_1/t + v_T/2 = (+100 km/h - 80 km/h) x= 20 km/h x

Voimme tehdä ilman vektorimerkintää. Huomaa alaosa: Kerrota molemmat oikealla on oltava vasemmalla puolella oleva.

Ja kun he ovat vastakkaiseen suuntaan? Nyt v_1/t = + 80 km/h ja V_2/t = -100 km/h, siksi v_T/2 = + 100 km/h. Auto -sinisen matkustaja näkee punaisen auton lähestyvän:

v_{1/2 =} v_1/t + v_T/2 = +80 km/h +100 km/h = 180 km/h

Suhteellinen liike kahdessa ja kolmessa ulottuvuudessa

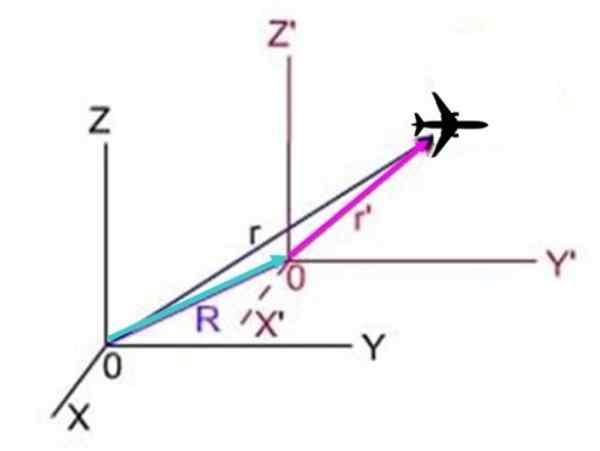
Seuraavassa järjestelmässä, r - Se on järjestelmästä nähty tason sijainti X ja z, r -'Se on asento järjestelmästä X ja z ' ja R - Se on järjestelmän sijainti palkkiolla järjestelmän suhteen ilman palkkioita. Kolme vektoria muodostavat kolmion, jossa R - + r -'= r -, siksi r -'= r - r.

Kuva 3.- Kone liikkuu suhteessa kahteen koordinaattijärjestelmään, puolestaan ​​yksi järjestelmistä liikkuu toiseen nähden.

Koska johdannainen aseman ajan suhteen on juuri nopeus, tulokset:

Voi palvella sinua: Parabolinen laukaus: Ominaisuudet, kaavat ja yhtälöt, esimerkit

v'= v - tai

Tässä yhtälössä v'Se on tason nopeus järjestelmän suhteen X ja z ', v on nopeus järjestelmän suhteen X ja z ja tai Se on pääjärjestelmän jatkuva nopeus järjestelmän suhteen ilman palkkioita.

-Liikunta ratkaistiin 2 

Kone on pohjoiseen suuntaan nopeudella suhteessa 240 km/h. Yhtäkkiä se alkaa puhaltaa tuulta lännestä itään 120 km: n nopeudella/ maan mukaan.

Löydä: a) Tason nopeus maapallon suhteen, b) Pilotin kokenut poikkeama c) korjaus, joka lentäjän on tehtävä voidakseen osoittaa suoraan pohjoiseen ja uusi nopeus maalle, kerran, kerran, kerran, kerran, kerran, kerran, kerran, kerran Korjaus on tehty.

Ratkaisu

A) Seuraavat elementit ovat: taso (a), maa (t) ja tuuli (v).

Koordinaattijärjestelmässä, jossa pohjoinen on + ja ja länsi-itäsuunta on + x, on annettu nopeudet ja niiden vastaava etiketti (alat):

v _Av = 240 km/h (+ja) v _V/t = 120 km/h (+x) v _A/t = ?

Riittävä vektorisumma on:

v _A/t = v _Av + v _V/t = 240 km/h (+ja) + 120 km/h (+x-A

Tämän vektorin suuruus on: v _A/t = (240 ²+ 120²-A^1/2 km/h = 268.3 km/h

b) θ = arctg (v _Av / v _V/t) = Arctg (240/120) = 63.4. Idästä pohjoiseen tai 26.Kuudes koillinen.

c) Jatkaksesi pohjoiseen tällä tuulella, sinun on osoitettava koneen keula luoteeseen, niin että tuuli työntää sen suoraan pohjoiseen. Tässä tapauksessa maasta havaitun tason nopeus on +: ssa ja vaikka lentokoneen nopeus tuulen suhteen on luoteis (se ei välttämättä ole 26.6.).

Voi palvella sinua: Bernoulli -lause

Kirjoittanut Pythagoras -lause:

v _A/t = (240 ²- 120²-A^1/2 km/h = 207.8 km/h

α = arctg (v _V/t / v _A/t ) = ARCTG (120/207.8) = 30. luoteis

-Liikunta ratkaistiin 3

Henkilö kestää 2 minuuttia kävellä liikkumattoman mekaanisen portaikon alas. Jos portaikko toimii, henkilö vie yhden minuutin mennäkseen edelleen. Kuinka kauan henkilö vie kävelyn ja portaikon ollessa käynnissä?

Ratkaisu

Otetaan huomioon kolme elementtiä: henkilö (p), portaikko (e) ja maa (s), joiden suhteelliset nopeudet ovat:

v_P/e : henkilön nopeus tikkaiden suhteen; v_ON: portaikon nopeus maahan; v_P/s: Henkilön nopeus suhteessa maahan.

Kuten kiinteä tarkkailija näkee maasta, portaikon (E) alentajalla on nopeus V _P/s antama:

v _P/s = v_P/e + v_ON

Positiivinen merkitys menee portaita alas. Olla t  Aika, joka kuluu kävelyyn ja Lens etäisyys. Henkilön suuruus V _P/s On:

v_P/s = L / t

t₁ On aika, joka kuluu kävelyyn pysäytetyn tikkaiden kanssa: V _P/e = L / t₁

Ja T₂ Se, joka vie sinut edelleen portaikkoon liikkeessä: V _ON = L / t₂

Ilmaisujen yhdistäminen:

L / t = l / t₁ + L / t₂

Numeeristen arvojen ja puhdistuksen korvaaminen t-

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Sitten t = 1/1.5 minuuttia = 40 sekuntia.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill. 84-88.
2. Figueroa, D. Fyysinen sarja tiedettä ja tekniikkaa. Osa 3. Painos. Kinematiikka. 199-232.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th. Ed. Prentice Hall. 62-64.
4. Suhteellinen liike. Toipunut: kurssit.Lumenarning.com
5. Wilson, J. 2011. Fysiikka 10. Pearson -koulutus. 166-168.