Kulmanopeuden keskimääräinen määritelmä ja kaavat, ratkaistut harjoitukset

Se Keskimääräinen kulmanopeus pyörimistä määritellään kulmana, jota pyörivät vektoriaikayksikön asennon avulla, joka kuvaa pyöreää liikettä. Kattotuulettimen terät (kuten kuvassa 1 esitetty) seuraa pyöreä liikettä ja sen keskimääräistä kulman nopeutta lasketaan ottamalla suhde käänneen kulman ja ajan, jolloin kyseinen kulma kulki.

Kiertoliikkeen noudattamat säännöt ovat tietyllä tavalla samanlaisia ​​kuin translaatioliikkeen jo sukulaiset. Ajatut etäisyydet voidaan mitata myös metreinä, mutta kulma -suuruudet ovat erityisen merkityksellisiä, koska ne helpottavat suuresti liikkeen kuvausta.

Kuvio 1. Tuulettimen terillä on kulmanopeus. Lähde: Pixabay

Kreikkalaisia ​​kirjaimia käytetään yleensä kulma -suuruuksiin ja latinalaisten kirjaimiin vastaaville lineaarisille suuruuksille.

[TOC]

Määritelmä ja kaavat

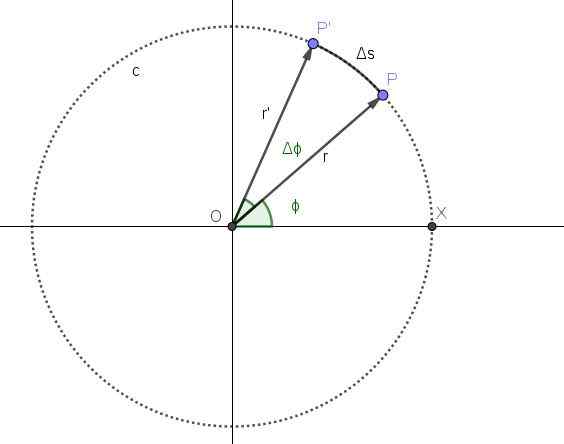
Kuvio 2 edustaa pisteen liikettä pyöreällä radalla C. Pisteen sijainti P vastaa hetkeä ja sitä hetkeä vastaava kulma -asema on ϕ. 

Hetkestä lähtien, kun aika on kulunut Δt. Siinä ajanjaksona pisteen uusi sijainti on P 'ja kulma -asema on lisännyt kulmaa Δϕ.

Kuva 2. Pisteen pyöreä liike. Lähde: Itse tehty

Keskimääräinen kulmanopeus ω on kulma kulunut aikayksikköä kohti, niin että osamäärä Δϕ/ΔT edustaa keskimääräistä kulmanopeutta hetkien T ja T+ΔT: n välillä:

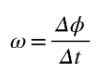
Koska kulma mitataan radiaaneina ja sekunneissa, keskimääräisen kulmanopeuden yhtenäisyys on rad/s. Jos haluat laskea kulmanopeus Juuri silloin t, sitten osamäärä Δϕ/ΔT on laskettava, kun ΔT ➡0.

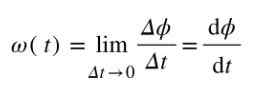Välikulman nopeuden mittayksikkö on myös rad/s.

Voi palvella sinua: 31 fysiikan voimantyyppiä ja niiden ominaisuuksia

Tasainen kierto

Kiertoliike on tasainen, jos kulma kulma on samana ajanjaksona, jos sitä havaitaan milloin tahansa, samana ajanjaksona. Jos kierto on tasaista, niin kulmanopeus milloin tahansa tapahtuu keskimääräisen kulmanopeuden kanssa.

Yhtenäisellä kiertoliikkeellä, jolloin täydellistä käännöstä kutsutaan ajanjakso Ja se on merkitty T: llä. 

Lisäksi kun kulma kulma on täynnä, se on 2π, joten yhtenäisessä kierroksessa kulmanopeus ω liittyy t -ajanjaksoon seuraavalla kaavalla:

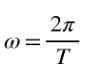
Se taajuus F yhtenäisestä kiertosta, kuten suhde käännösten lukumäärän ja niiden matkustamiseen käytetyn ajan välillä, ts. Aikana Δt on silloin taajuus:

F = n/Δt

Kierroksena (n = 1) sitä kuljetetaan aikaan t (ajanjakso), seuraava suhde on käytettävissä:

F = 1/t

Toisin sanoen yhtenäisessä kiertokunnassa kulmanopeus liittyy suhteiden kautta tapahtuvaan taajuuteen:

Ω = 2π ・ f

Kulmanopeuden ja lineaarisen nopeuden välinen suhde

Lineaarinen nopeus v, Se on osamäärä kuluneen matkan ja sen kuluttamiseen käytetyn ajanjakson välillä. Kuviossa 2 ajettu etäisyys on kaaren ΔS pituus. 

Kaari ΔS on verrannollinen kulmaan kulkeneen Δϕ ja radio r täyttäen seuraavan suhteen:

ΔS = r ・ Δϕ

Aina kun δϕ mitataan radiaaneina.

Jos jaamme edellisen lausekkeen ajanjakson ΔT välillä, saamme:

(ΔS/Δt) = r ・ (Δϕ/ΔT)

Ensimmäinen jäsensuhde on toisen jäsenen lineaarinen nopeus ja jakaminen keskimääräinen kulmanopeus:

Voi palvella sinua: Mount Olympus (Mars)

v = r ・ ω

Ratkaisut

-Harjoitus 1

Kuvassa 1 esitettyjen kattopuhaltimien kärjet liikkuvat nopeudella 5 m/s ja terät ovat 40 cm sädettä.

Näiden tietojen kanssa lasketaan: i) pyörän keskimääräinen kulmanopeus, ii) pyörien lukumäärä sekunnissa, iii) ajanjakso sekunneissa.

Ratkaisu 

i) lineaarinen nopeus on v = 5 m/s.

Radio on r = 0,40 m.

Lineaarisen nopeuden ja kulmanopeuden välisestä suhteesta puhdistamme jälkimmäisen:

v = r ・ ω => ω = V/r = (5 m/s)/(0,40 m) = 12,57 rad/s

ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 käännöstä / s

iii) t = 1 / f = 1 / (2 kierrosta / s) = 0,5 s kierrosta kohden.

-Harjoitus 2

Lelu kävelee 2 m: n säteen pyöreällä radalla. 0: ssa sen kulma -asema on 0 rad, mutta ajan kuluttua sen kulma -asema on

φ (t) = 2 ・ t .

Näiden tietojen kanssa 

i) Laske keskimääräinen kulmanopeus seuraavilla aikaväleillä [0s, 0.5S]; [0.5S, 1.0s]; [1.0, 1.5S] ja lopulta ajanjaksolla [0.0, 1.5S]. 

ii) Osan I tulosten perusteella mitä voidaan sanoa liikkeestä?

iii) Määritä keskimääräinen lineaarinen nopeus samassa jakson iissä)

iv) Löydä kulmanopeus ja lineaarinen nopeus milloin tahansa.

Ratkaisu 

i) Keskimääräinen kulmanopeus annetaan seuraavalla kaavalla:

Jatkamme kulman laskemista ja jokaisessa aikavälillä kului ajanjakso.

Intervalli 1: Δϕ = ϕ (0.5S) - ϕ (0.0s) = 2 (rad/s)*0.5S - 2 (rad/s)*0.0s = 1.0 rad

                   Δt = 0.5S - 0.0s = 0.5s

Voi palvella sinua: BTU (lämpöyksikkö): ekvivalenssit, käytöt, esimerkit

                   Ω = Δϕ/ΔT = 1.0Rad/0.5S = 2.0 rad/s

Väli 2: Δϕ = ϕ (1.0s) - ϕ (0.5S) = 2 (rad/s)*1.0s - 2 (rad/s)*0.5S = 1.0 rad

                   Δt = 1.0s - 0.5S = 0.5s

                   Ω = Δϕ/ΔT = 1.0Rad/0.5S = 2.0 rad/s

Väli 3: Δϕ = ϕ (1.5S) - ϕ (1.0s) = 2 (rad/s)*1.5S - 2 (rad/s)*1.0s = 1.0 rad

                   Δt = 1.5S - 1.0s = 0.5s

                   Ω = Δϕ/ΔT = 1.0Rad/0.5S = 2.0 rad/s

Väli 4: Δϕ = ϕ (1.5S) - ϕ (0.0s) = 2 (rad/s)*1.5S - 2 (rad/s)*0.0s = 3.0 rad

                   Δt = 1.5S - 0.0s = 1.5s

                   Ω = Δϕ/ΔT = 3.0RAD/1.5S = 2.0 rad/s

ii) Edellisten tulosten vuoksi, joissa keskimääräinen kulmanopeus laskettiin eri aikaväleillä, sama tulos saadaan aina. Näyttää siltä, ​​että se on tasainen pyöreä liike. Nämä tulokset eivät kuitenkaan ole vakuuttavia.

Tapa varmistaa, että johtopäätös on laskea keskimääräinen kulmanopeus mielivaltaisella aikavälillä [t, t -t)

                                     Δt = t ' - t

                                     Ω = Δϕ/Δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

Tämä tarkoittaa, että lelun kävelymatkalla on vakio keskimääräinen kulma nopeus 2 rad/s millä tahansa tarkasteltavana ajanjaksolla. Mutta voit mennä pidemmälle, jos välitön kulmanopeus lasketaan:

Tätä tulkitaan leluautolla jatkuvasti kulmanopeus = 2 rad/s.

Viitteet

1. Giancoli, D. Fysiikka. Periaatteet hakemuksissa. 6. painos. Prentice Hall. 30-45.
2. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen. 117.
3. Resnick, r. (1999). Fyysinen. Osa 1. Kolmas painos espanjaksi. Meksiko. Mannertoimitusyhtiö S.-Lla. C: n.V. 33-52.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Painos. Meksiko. Cengage Learning Editors. 32-55.
5. Wikipedia. Kulmanopeus. Toipunut: Wikipedia.com