Karnot -kone

Mikä on Carnot -kone?

Se Karnot -kone Se on ihanteellinen syklinen malli, jossa lämpöä käytetään työn tekemiseen. Järjestelmä voidaan ymmärtää mäntänä, joka liikkuu sylinterin sisällä painettaessa kaasua. Ranskan fyysikko ja insinööri Nicolas Leonard Sadi Carnot on käytetty Carnotin sykli.

Carnot ilmoitti tämän syklin 1800 -luvun alkupuolella. Koneelle altistetaan neljä tilavariaatiota, vuorottelevia olosuhteita, kuten vakio lämpötila ja paine, joissa tilavuuden vaihtelu käy ilmi kaasun puristamisessa ja laajentamisessa.

Kaavat

Carnotin mukaan ihanteellisen koneen alistaminen lämpötila- ja painevaihteluihin on mahdollista maksimoida saatu suorituskyky.

Carnot -sykli on analysoitava erikseen jokaisessa sen neljässä vaiheessa: isoterminen laajennus, adiabaattinen laajennus, isoterminen puristus ja adiabaattinen puristus.

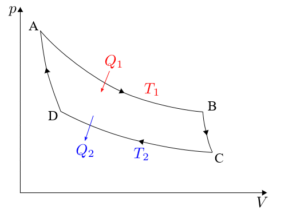
Kaavoihin liittyvät kaavat Carnot -koneessa käytetyn syklin vaiheessa on yksityiskohtaisesti esitetty.

Isoterminen laajennus (A → B)

Tämän vaiheen tilat ovat seuraavat:

• Kaasun tilavuus: Se siirtyy vähimmäismäärästä keskimääräiseen tilavuuteen.
• Koneen lämpötila: vakio lämpötila T1, korkea arvo (T1> T2).
• Koneenpaine: Laskeudu P1: stä P2: een.

Isoterminen prosessi tarkoittaa, että lämpötila T1 ei vaihtele tämän vaiheen aikana. Lämmönsiirto indusoi kaasun laajenemista, joka indusoi männän liikkeen ja tuottaa mekaanista työtä.

Laajentuessaan kaasulla on tietty taipumus jäähtyä. Se kuitenkin absorboi lämpötilan lähteen lähettämän lämpöä ja sen laajentumisen aikana se ylläpitää vakio lämpötilaa.

Voi palvella sinua: mikä on lineaarinen nopeus? (Ratkaistujen harjoitusten kanssa)

Koska lämpötila pysyy vakiona tämän prosessin aikana, kaasun sisäinen energia ei muutu ja kaikki kaasun absorboimat lämpöä muuttuu tehokkaasti työksi. Niin:

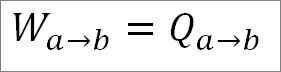
Toisaalta tämän syklin tämän vaiheen lopussa on myös mahdollista saada painearvo käyttämällä sille ihanteellista kaasuyhtälöä. Tällä tavalla sinulla on seuraavat:

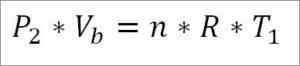
Tässä ilmaisussa:

• P₂: Paine vaiheen lopussa.
• V_{b -}: Tilavuus kohdassa B.
• N: Kaasujen lukumäärä.
• V: Ihanteellisten kaasujen yleinen vakio. R = 0,082 (atm*litra)/(moolit*k).
• T1: Absoluuttinen alkulämpötila, Kelvin -asteet.

Adiabaattinen laajennus (B → C)

Tämän prosessin vaiheessa kaasun laajeneminen suoritetaan ilman tarvetta vaihtaa lämpöä. Tällä tavoin tilat on yksityiskohtaisesti esitetty:

• Kaasun tilavuus: Se siirtyy keskimääräisestä tilavuudesta enimmäismäärään.
• Koneen lämpötila: Laskeudu T1: stä T2: een.
• Koneenpaine: vakio P2 -paine.

Adiabaattinen prosessi tarkoittaa, että P2 -paine ei vaihtele tämän vaiheen aikana. Lämpötila laskee ja kaasu kasvaa edelleen, kunnes se saavuttaa sen tilavuuden enimmäismäärän; toisin sanoen mäntä saavuttaa huipun.

Tässä tapauksessa tehty työ tulee kaasun sisäisestä energiasta ja sen arvo on negatiivinen, koska energia vähenee tämän prosessin aikana.

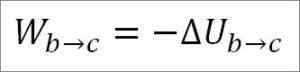
Olettaen, että se on ihanteellinen kaasu, väitetään, että kaasumolekyyleissä on vain kineettinen energia. Termodynamiikan periaatteiden mukaan tämä voidaan päätellä seuraavalla kaavalla:

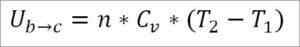
Tässä kaavassa:

• ∆U_{b → c}: Ihanteellisen kaasun sisäinen energian vaihtelu pisteiden B ja C välillä.
• N: Kaasujen lukumäärä.
• CV: kaasumoolinen lämpökapasiteetti.
• T1: Absoluuttinen alkulämpötila, Kelvin -asteet.
• T2: Absoluuttinen lopullinen lämpötila, Kelvin -asteet.

Voi palvella sinua: isobarinen prosessi: kaavat, yhtälöt, kokeet, harjoitukset

Isoterminen pakkaus (C → D)

Tässä vaiheessa kaasun puristus alkaa; toisin sanoen mäntä mobilisoidaan sylinteriin, jonka kanssa kaasu supistuu sen määrän.

Tässä prosessissa ominaiset olosuhteet on yksityiskohtaisesti yksityiskohtaisesti:

• Kaasun tilavuus: Se siirtyy enimmäismäärästä välitilavuuteen.
• Koneen lämpötila: vakio lämpötila T2, alennettu arvo (T2 < T1).
• Koneenpaine: Kasvu P2: sta P1: ään.

Kaasun paine kasvaa tässä, joten se alkaa puristaa. Lämpötila pysyy kuitenkin vakiona, ja siksi kaasun sisäinen energian vaihtelu on nolla.

Analogi isotermisen laajentumisen suhteen, tehty työ on yhtä suuri kuin järjestelmän lämpö. Niin:

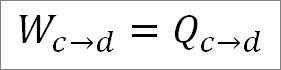
On myös mahdollista löytää paine tässä vaiheessa käyttämällä ihanteellista kaasuyhtälöä.

Adiabaattinen puristus (D → A)

Tämä on prosessin viimeinen vaihe, jossa järjestelmä palaa alkuperäisiin olosuhteisiinsa. Tätä varten tarkastellaan seuraavia ehtoja:

• Kaasun tilavuus: Se siirtyy välitilavuudesta vähimmäistilavuuteen.
• Koneen lämpötila: Kasvu T2: sta T1: ään.
• Koneenpaine: vakiopaine P1.

Edellisessä vaiheessa järjestelmään sisällytetty lämmönlähde poistetaan, joten ihanteellinen kaasu nostaa lämpötilansa sillä välin paine pysyy vakiona.

Kaasu palaa alkuperäiseen lämpötilaolosuhteisiin (T1) ja sen tilavuudella (minimi). Tehty työ tulee jälleen kaasun sisäisestä energiasta, joten sinun on:

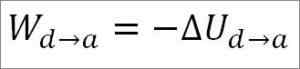
Samoin kuin adiabaattisen laajentumisen tapaus, on mahdollista saada kaasun energian vaihtelu seuraavan matemaattisen ekspression avulla:

Voi palvella sinua: kalsiumfluori (CAF2): rakenne, ominaisuudet, käyttötarkoitukset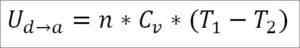

Kuinka Carnot -kone toimii?

Carnot -kone toimii moottorina, jossa suorituskyky maksimoidaan isotermisten ja adiabaattisten prosessien variaatiolla, vuorotellen ihanteellisen kaasun laajenemisen ja ymmärtämisen vaiheet.

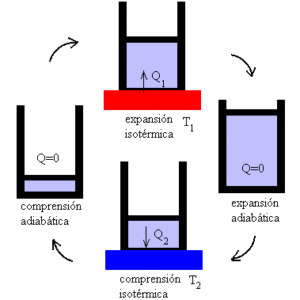
Mekanismi voidaan ymmärtää ihanteellisena laitteena, joka harjoittaa lämmönvaihteluita altistuneita, kun otetaan huomioon kaksi lämpötilan valokeilaa.

Ensimmäisessä tarkennuksessa järjestelmä altistuu T1 -lämpötilaan. Se on korkea lämpötila, joka kohdistaa järjestelmän stressiin ja tuottaa kaasun laajentumista.

Tämä puolestaan ​​johtaa mekaanisen työn suorittamiseen, joka sallii männän mobilisoinnin sylinteristä ja jonka rajan on mahdollista vain adiabaattisella laajentumisella.

Sitten tulee toinen painopiste, jossa järjestelmä altistuu T2 -lämpötilaan, vähemmän kuin T1; eli mekanismi on jäähdytetty.

Tämä indusoi lämmön uuttamisen ja kaasun murskauksen, joka saavuttaa alkuperäisen tilavuutensa adiabaattisen puristuksen jälkeen.

Sovellukset

Carnot -konetta on käytetty laajasti sen panoksen ansiosta termodynamiikan tärkeimpien näkökohtien ymmärtämisessä.

Tämän mallin avulla voit ymmärtää selkeästi lämpötilan ja paineen muutosten alaisia ​​ihanteellisten kaasujen variaatioita, mikä on referenssimenetelmä todellisten moottorien suunnittelussa.