Euler -menetelmä menettelyn ja harjoitusten käyttöön

Hän Euler -menetelmä Se on perusteellisin ja yksinkertaisin menettelyistä, joita käytetään likimääräisten numeeristen ratkaisujen löytämiseen ensimmäisen asteen tavalliselle differentiaaliyhtälölle.

Tavallinen differentiaaliyhtälö (EDO) on yhtälö, joka liittyy yhden riippumattoman muuttujan tuntemattomaan funktioon sen johdannaisilla.

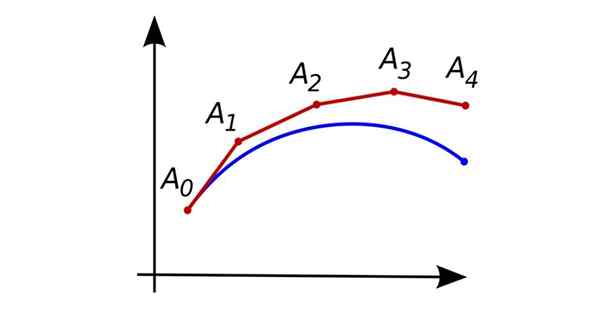
Peräkkäiset lähestymistavat Eulerin menetelmällä. Lähde: Oleg Alexandrov [julkinen alue]

Jos yhtälössä esiintyvä suurin johdannainen on yksi aste, niin se on ensimmäisen asteen tavallinen differentiaaliyhtälö.

Yleisin tapa kirjoittaa ensimmäisen asteen yhtälö on:

Alkuedelläni:

x = x_{0 -}

y = y_{0 -}

[TOC]

Mikä on Eulerin menetelmä?

Euler -menetelmän idea on löytää numeerinen ratkaisu differentiaaliyhtälöön x: n välillä_{0 -} ja x_F .

Ensinnäkin, aikaväli n+1 pisteessä on eri mieltä:

x_{0 -}, x₁, x₂, x₃…, X_n

Jotka saadaan näin:
x_Yllyttää= x_{0 -}+Ihas

Missä H on alaluokkien leveys tai vaihe:

Mitä suurempi luku n tulos on tarkempi, mutta tarvitaan suurempi määrä pisteitä kattamaan väliaika, jossa etsimme ratkaisua ja laskenta -aika kasvaa.

Alkutilalla on myös mahdollista tuntea johdannainen alussa:

ja '(x_jompikumpi) = f (x_jompikumpi, ja_jompikumpi-A

Tämä johdannainen edustaa linjan kaltevuutta tangentin funktiokäyrälle y (x) tarkasti pisteessä:

AO = (x_jompikumpi, ja_jompikumpi-A

Sitten funktion y (x) arvon likimääräinen ennuste tehdään seuraavassa kohdassa:

ja (x₁) ≈ ja₁

ja_1 = ja_jompikumpi +(x₁- x_jompikumpi) f (x_jompikumpi, ja_jompikumpi) = y_{jompikumpi +} H F (x_jompikumpi, ja_jompikumpi-A

Seuraava likimääräinen kohta liuoksessa, joka vastaa:

-Lla₁ = (x₁, ja₁-A

Menettely toistetaan peräkkäisten pisteiden saamiseksi

Voi palvella sinua: Logaritminen funktio: Ominaisuudet, esimerkit, harjoitukset

-Lla₂, -Lla₃…, X_n

Alussa esitetyssä kuvassa sininen käyrä edustaa erilaisen yhtälön tarkkaa ratkaisua, ja punainen edustaa peräkkäisiä likimääräisiä pisteitä, jotka on saatu Euler -menettelyllä.

Ratkaisut

Harjoitus 1

Yllyttää) Ole differentiaaliyhtälö:

Alkutilassa x = a = 0; ja_-lla= 1

Hanki likimääräinen ratkaisu käyttämällä Euler -menetelmää ja Koordinaatissa x = b = 0.5, väliaika [a, b] n = 5 osassa.

Ratkaisu

Numeeriset tulokset on esitetty seuraavasti:

Missä päätellään, että ratkaisu ja arvo 0.5 on 1.4851.

Huomaa: Käytettyjen laskelmien toteuttamiseksi SMATH -Studio, Ilmainen ilmainen käyttöohjelma.

Harjoitus 2

II) Jatka harjoituksen i differentiaaliyhtälöllä), etsi tarkka ratkaisu ja vertaa sitä Euler -menetelmällä saatuun tulokseen. Etsi virhe tai ero tarkan tuloksen ja likimääräisen välillä.

Ratkaisu

Alkutilassa x = a = 0; ja_-lla= 1
Tarkkaa ratkaisua ei ole kovin vaikea löytää. On tiedossa, että Sen (x) -funktion johdannainen on cos (x) -toiminto. Siksi ratkaisu y (x) on:

ja (x) = sin x + c

Alkuolan ja (0) = 1: n täyttämiseksi vakion C on oltava 1 arvoinen. Seuraavaksi tarkkaa tulosta verrataan likimääräiseen:

Johtopäätöksenä on, että lasketulla aikavälillä lähestymistavalla on kolme merkittävää tarkkuuskuvaa.

Harjoitus 3

III) Harkitse alla olevia differentiaaliyhtälöitä ja sen alkuolosuhteita:

ja '(x) =- y²

Alkuolosuhteella x_{0 -} = 0; ja_{0 -} = 1

Löydä liuoksen likimääräiset arvot Euler -menetelmällä ja (x) Välein x = [0, 1.5]. Käyttää vaihetta H = 0.1.

Ratkaisu

Eulerin menetelmä on osoitettu käytettäväksi laskentataulukon kanssa. Tässä tapauksessa käytämme laskentataulukkoa Geogebra, Ilmainen ja ilmainen käyttöohjelma.

Se voi palvella sinua: Yhdistetty suhteellisuus: Selitys, kolme yhdistelmäsääntöä, harjoituksia

Kolme saraketta (A, B, C) on esitetty kuvan laskentataulukossa x , Toinen sarake edustaa muuttujaa ja, ja kolmas sarake johdannainen ja'.

Rivi 2 sisältää alkuperäiset arvot X, JA, JA' .

Arvon arvo 0.1 Se on sijoitettu absoluuttiseen sijaintikennoon ($ d 4 dollaria).

Alkuperäinen Y0 -arvo on solussa B2 ja Y1 solussa B3. Laskea ja₁ Kaavaa käytetään:

ja_1 = ja_jompikumpi +(x₁- x_jompikumpi) f (x_jompikumpi, ja_jompikumpi) = y_{jompikumpi +} H F (x_jompikumpi, ja_jompikumpi-A

Tämä laskentataulukon kaava olisi numero B3: = B2 + $ d 4 dollaria * C3.

Samoin y2 olisi solussa B4 ja sen kaava esitetään seuraavassa kuvassa:

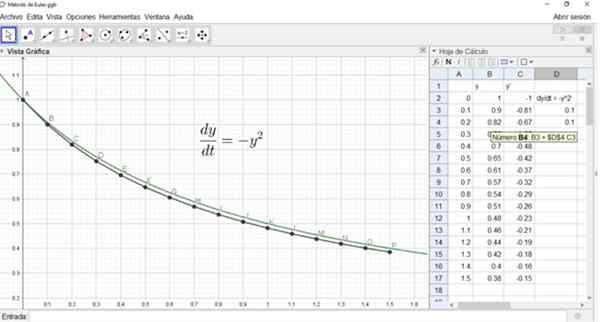
Kuvio näyttää myös tarkan liuoksen kaavion ja likimääräisen ratkaisun pisteet A, B, ..., P Euler -menetelmän avulla.

Newton Dynamics ja Eulerin menetelmä

Klassisen dynamiikan on kehittänyt Isaac Newton (1643 - 1727). Leonard Eulerin (1707 - 1783) alkuperäinen motivaatio kehittää menetelmää oli juuri Newtonin toisen lain yhtälön ratkaiseminen erilaisissa fyysisissä tilanteissa.

Newtonin toinen laki ilmaistaan ​​usein toissijaisena differentiaaliyhtälönä:

Missä x edustaa esineen sijaintia tällä hetkellä t. Tällä esineellä on massa m ja joutuu voimaan F. Toiminto F Se liittyy vahvuuteen ja massaan seuraavasti:

 Vaikka Euler -menetelmä on periaatteessa suunniteltu ratkaisemaan ensimmäisen asteen differentiaaliyhtälöt, se on helposti laajennettavissa toiseen asteen tapaukseen, koska se vastaa kahden ensimmäisen asteen yhtälön järjestelmää.

Se voi palvella sinua: analyyttinen geometria

Euler -menetelmän soveltamiseksi vaaditaan alkuperäiset aikaarvot t, nopeus v asento x.

Seuraava taulukko selittää, kuinka aloittaminen alkuperäisistä arvoista T1, V1, X1 on saanut V2 -nopeuden likiarvoa ja X2 Eulerin menetelmässä.

Harjoitus 4

IV) Yksi mekaniikan perusongelmista on joustavan vakion kuksen (tai kevään) massa -lohko Massan (tai kevään) lohkoon.

Newtonin toinen laki tästä ongelmasta olisi tällainen:

Tässä esimerkissä sen yksinkertaistamiseksi otetaan m = 1 ja k = 1. Löydä likimääräisiä ratkaisuja asentoon x Ja nopeus v Eulerin menetelmällä aikavälillä [0, π/2], joka on jakamassa välein 12 osassa.

Ota 0 alkuperäisenä momentina, alustavan nopeuden 0 ja alkuasento 1.

Ratkaisu

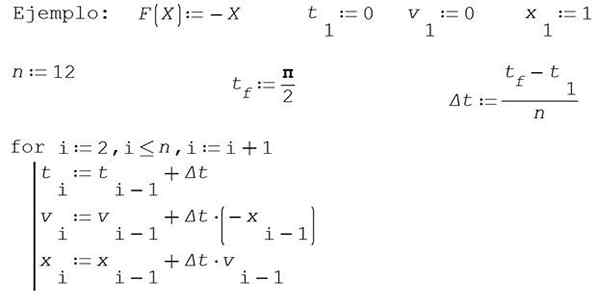
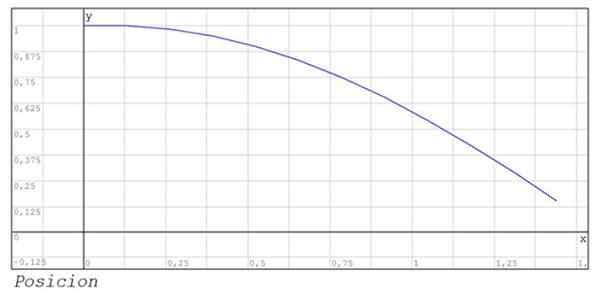
Numeeriset tulokset on esitetty seuraavassa taulukossa:

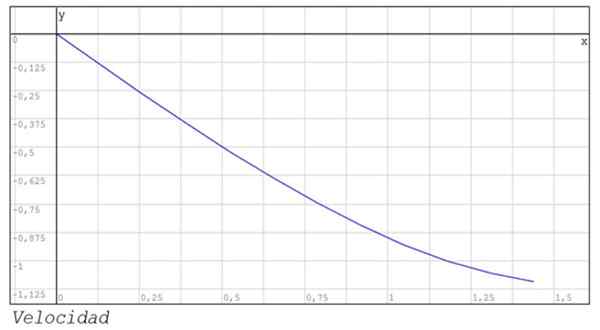
Näytetään myös aseman grafiikka ja nopeus infttien 0 ja 1 välillä.44.

Ehdotetut harjoitukset kotiin

Harjoitus 1

Käytä laskentataulukkoa määrittääksesi likimääräinen ratkaisu käyttämällä Euler -menetelmää differentiaaliyhtälöön:

ja '= -exp (-y) alkuolosuhteilla x = 0, y = -1 aikavälillä x = [0, 1]

Aloita askeleella 0,1. Kuvaa tulos.

Harjoitus 2

Löydä laskentataulukkoa, etsi numeeriset ratkaisut seuraavan toisen asteen yhtälöön, missä ja se on riippumattoman muuttujan T funktio.

ja "= - 1/y² alkutilassa t = 0; y (0) = 0,5; ja '(0) = 0

Löydä ratkaisu aikavälillä [0,5; 1,0] käyttämällä vaiheen 0,05.

Kuvaa tulos: ja vs t; ja 'vs t

Viitteet

1. Eurlerin menetelmä.Otettu Wikipediasta.org
2. Euler -ratkaisija. Otettu.Hauta.com