Unkarin menetelmä mitä koostuu, esimerkki

Hän Unkarin menetelmä Se on algoritmi, jota käytetään allokointiongelmissa, kun haluat minimoida kustannukset. Eli sitä käytetään vähimmäiskustannusten löytämiseen määrittämällä useita ihmisiä erilaisiin toimintoihin alhaisimpien kustannusten perusteella. Jokainen toiminta on osoitettava toiselle henkilölle.

Tehtävän ongelma on erityinen lineaarinen ohjelmointiongelma, jossa tavoitteena on minimoida useiden ihmisten työsuhde tai aika suorittaa työ.

Lähde: Pixabay.com

Yksi jakamisongelman tärkeistä ominaisuuksista on, että vain yksi työ (tai työntekijä) on osoitettu koneelle (tai projekti).

Tämän menetelmän on kehittänyt unkarilainen matemaatikko d. Konig. Tästä syystä se tunnetaan unkarilaisena menetelmänä jakamisongelmiin. Se tunnetaan myös nimellä Kuhn-Munkres -määritysalgoritmi.

Mikä tahansa allokointiongelma voidaan ratkaista helposti soveltamalla tätä menetelmää, joka koostuu kahdesta vaiheesta:

- Ensimmäisen vaiheen kanssa vähenee rivejä ja pylväsvähennyksiä.

- Toisessa vaiheessa iteratiivisen emäksen liuos on optimoitu.

[TOC]

Mikä on unkarilainen menetelmä?

Unkarin menetelmä koostuu neljästä askelta. Kaksi ensimmäistä vaihetta suoritetaan vain kerran, kun taas vaiheet 3 ja 4 toistetaan, kunnes ne löytävät optimaalisen tehtävän.

Sitä pidetään neliömatriisin N: n neliömatriisissa N: llä, jonka on sisällettävä vain ei -negatiivisia elementtejä.

Tietyn ongelman vuoksi, jos matriisissa olevien rivien lukumäärä ei ole yhtä suuri kuin sarakkeiden lukumäärä, kuvitteellinen rivi tai kuvitteellinen sarake on lisättävä tapauksesta riippuen. Näiden kuvitteellisten solujen toimeksiantokustannukset osoitetaan aina nollaan.

Vaihe 1: Vähennä kunkin rivin minimit

Jokaiselle matriisin riville elementti valitaan kunkin elementin alhaisimmalla arvolla ja vähennyksellä.

Voi palvella sinua: mikä on nykyinen omaisuus? (Esimerkkejä)

Vaihe 2: Vähennä kunkin sarakkeen minimit

Samoin elementti, jolla on alhaisin arvo, valitaan jokaiselle sarakkeelle ja vähennetään se jokaisesta kyseisen sarakkeen elementistä.

Vaihe 3: Peitä kaikki nollat, joissa on vähimmäismäärä linjoja

Kaikki nollat ​​on peitettävä matriisiin, joka johtuu vaiheesta 2 käyttämällä vähimmäismäärää vaaka- ja pystysuoria viivoja joko rivien tai sarakkeiden avulla.

Jos kaikkien nollien peittämiseen tarvitaan kokonaisviivoja, jotka ovat N, joka on yhtä suuri kuin matriisin koko N / N / n, nollat ​​ovat optimaalinen ja siksi algoritmi pysähtyy.

Muuten, jos vaaditaan vähemmän viivoja kattamaan kaikki matriisin nollat, se jatkuu vaiheessa 4.

Vaihe 4: Luo ylimääräisiä nollia

Matriisin vähiten elementti (nimeltään k) valitaan, jota ei katettu yhdellä vaiheessa 3 tehdyistä linjoista.

Kaikkien elementtien arvo, joita linjat eivät kata, vähennetään. Myöhemmin K: n arvo lisätään kaikkiin elementteihin, jotka peitetään kahden viivan leikkauspisteellä.

Yhden rivin peittämät elementit jätetään sellaisenaan. Tämän vaiheen suorittamisen jälkeen palaat vaiheeseen 3.

Optimaalinen tehtävä

Kun algoritmi on pysäytetty vaiheessa 3, valittiin nollajoukko siten, että jokaisella rivillä ja jokaisessa sarakkeessa on vain yksi valittu nolla.

Jos tässä valintaprosessissa ei ole yhtä nollaa peräkkäin tai sarakkeessa, yksi niistä nollaista sitten valitaan. Jäljellä olevat nollat ​​poistetaan kyseisessä sarakkeessa tai rivissä, toistaen saman myös muille tehtäville.

Se voi palvella sinua: makrolokalisaatio

Jos nollaa ei ole yhtä allokointia, tarkoittaa, että ratkaisuja on useita. Kustannukset pysyvät kuitenkin samoina eri allokaatiojoukkojen kohdalla.

Kaikki lisätty kuvitteelliset rivi tai sarakkeet poistetaan. Tässä lopullisessa matriisissa valitut nollat ​​vastaavat alkuperäisessä matriisissa tarvittavaa ihanteellista määritystä.

Esimerkki

Harkitse yritystä, jossa on neljä toimintaa (A1, A2, A3, A4), jotka neljän työntekijän on toteutettava (T1, T2, T3, T4). Työntekijää kohden on määritettävä.

Seuraava matriisi näyttää tietyn työntekijän määrittämisen kustannukset tiettyyn toimintaan. Tavoitteena on minimoida näistä neljästä toiminnasta koostuvan tehtävän kokonaiskustannukset.

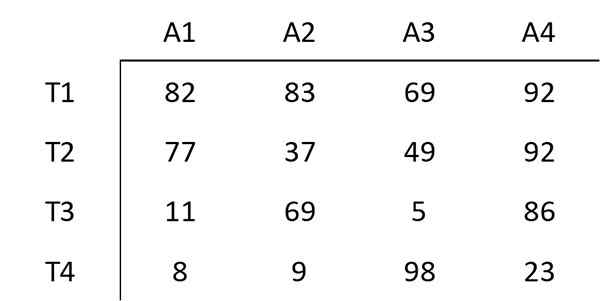
Vaihe 1: Vähennä kunkin rivin minimit

Elementti alkaa kyseisen rivin muiden elementtien kunkin rivin minimiarvolla. Esimerkiksi ensimmäisen rivin pienin elementti on 69. Siksi 69 jokaisesta elementistä vähennetään ensimmäisessä rivissä. Tuloksena oleva matriisi on:

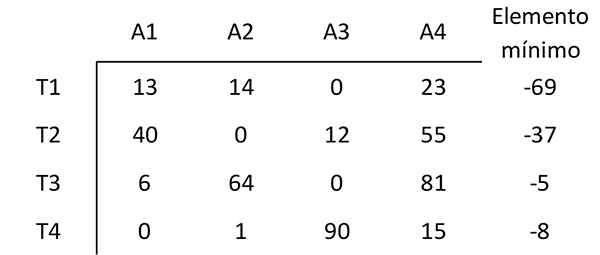
Vaihe 2: Vähennä kunkin sarakkeen minimit

Samalla tavalla elementti vähennetään kyseisen sarakkeen muiden elementtien pienimmän arvon kanssa seuraavan matriisin hankkiminen:

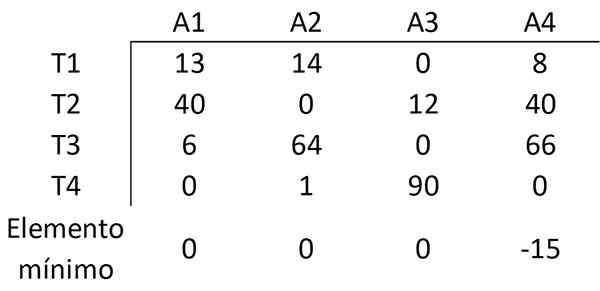
Vaihe 3: Peitä kaikki nollat, joissa on vähimmäismäärä linjoja

Nyt määritetään vähimmäismäärä linjoja (vaakasuora tai pystysuuntainen), jotka vaaditaan kaikkien matriisin nollan peittämiseksi. Kaikki nollat ​​voidaan peittää 3 rivillä:

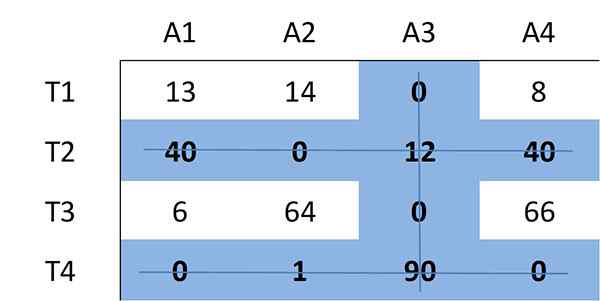
Koska vaadittujen linjojen lukumäärä on kolme ja on pienempi kuin matriisin koko (n = 4), se jatkuu vaiheessa 4.

Voi palvella sinua: Projektinhallinta: Mikä on, vaiheet, tavoitteet, esimerkit

Vaihe 4: Luo ylimääräisiä nollia

Alin elementti, jota linjat eivät kata, valitaan, jonka arvo on 6. Kaikkien ei -peittämättömien elementtien arvo vähennetään ja tämä sama arvo lisätään kaikkiin kahden rivin risteyksen peittämiin elementteihin. Tämä johtaa seuraavaan matriisiin:

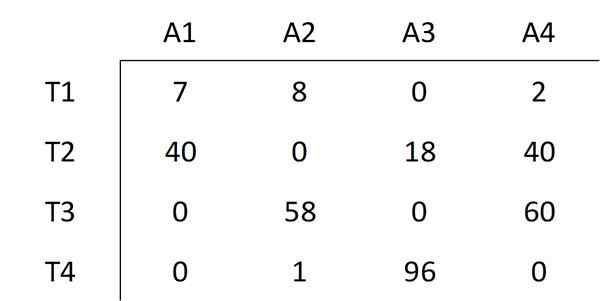
Kuten Unkarin menetelmä on osoitettu, askel numero kolme on suoritettava uudelleen.

Vaihe 3 (toisto)

Jälleen vähimmäismäärä rivejä, joita tarvitaan kaikkien matriisin nollan peittämiseen, määritetään. Tällä kertaa vaaditaan neljä riviä:

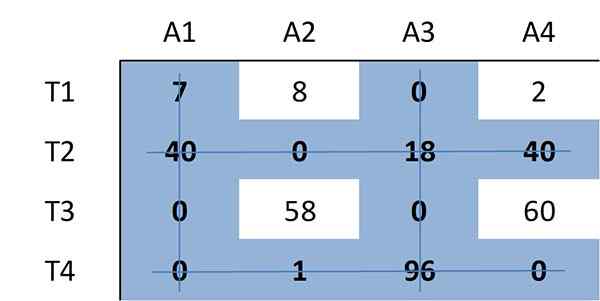
Koska vaadittavien linjojen lukumäärä on 4, yhtä suuri kuin matriisin koko (n = 4), matriisissa on optimaalinen määritys nollat. Siksi algoritmi pysähtyy.

Optimaalinen tehtävä

Kuten menetelmä on osoittanut, seuraavista nollasta valmistettu valinta vastaa optimaalista määritystä:

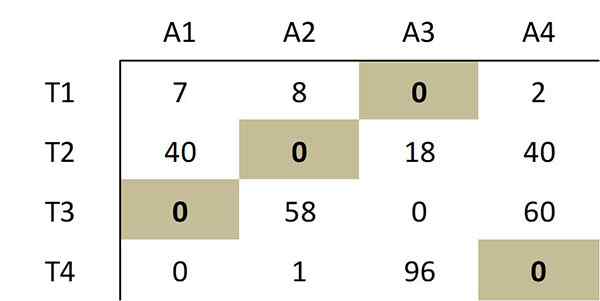
Tämä nollavalinta vastaa seuraavaa optimaalista allokointia alkuperäisessä kustannusmatriisissa:

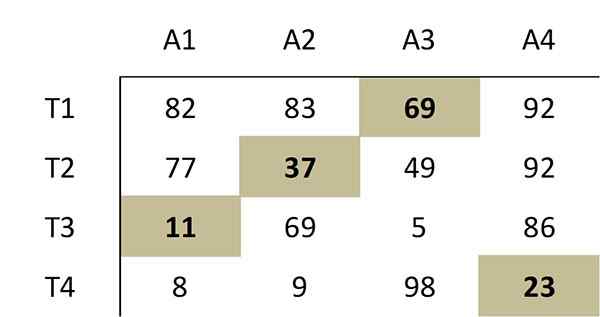
Siksi työntekijän 1 on suoritettava aktiviteetti 3, työntekijä 2, aktiviteetti 2, työntekijä 3, aktiviteetti 1 ja työntekijän 4 on suoritettava aktiviteetti 4. Tämän optimaalisen määrityksen kokonaiskustannukset ovat 69+37+11+23 = 140.

Viitteet

1. Unkarin algoritmi (2019). Unkarin algoritmi. Otettu: Unkarianalgoritmi.com.
2. Tutkimus (2019). Unkarin algoritmin käyttäminen tehtäväongelmien ratkaisemiseksi. Otettu: Opiskelu.com.
3. Viisaustyöt (2018). Unkarin menetelmä määritysongelman ratkaisemiseksi - kvantitatiiviset tekniikat johtamiselle. Otettu: Wisdomjobs.com.
4. Geeks Geeksille (2019). Unkarin algoritmi toimeksiannon ongelmaan. Otettu: Geeksforgeeks.org.
5. Karleight Moore, Nathan Landman (2019). Unkarin maksimaalinen sovitusalgoritmi. Loistava. Otettu: Brilliant.org.