Ympyrän määritelmän rekisteröity kulma, lauseet, esimerkit

Hän Rekisteröity ympyrän kulma Se on se, jolla on kehä ja sen puoliksi. Seurauksena on, että rekisteröity kulma on aina kupera tai tasainen.

Kuviossa 1 on edustettuna niiden vastaaviin kehoihin rekisteröityjä kulmia. Kulma ∠EDF on rekisteröity ottamalla sen kärkikortiksi D ja sen kaksi puolijuoteilijää [OF) ja [df), joka kuivattaa kehä. 

Kuvio 1. Useita kirjoitettuja kulmia niiden ympärysmittaisuuksista. Lähde: f. Zapata geogebralla.

Samoin kulma ∠HGI on rekisteröity, jotta sen kärki on kehossa ja sen kuivat sivut samaan.

Kulmat ∠KJR ja ∠UT on myös rekisteröity kehällä. Ensimmäisellä on yksi sekaantin puoli ja toinen tangentti, kun taas toisella on kaksi puolta ympärysmielle, muodostaen tasaisen tasomerkin (180º) (180º).

Jotkut kirjoittajat kutsuvat puoliksi kirjoitettua kulmaa sille, jolla on yksi hänen puolistaan ​​tangentti kehälle, mutta tässä artikkelissa häntä pidetään rekisteröidyksi.

Mikä tahansa rekisteröity kulma määrittelee tai subtendistaa samaan liittyvän kaaren. Esimerkiksi kuvassa 2 rekisteröity kulma ∠ABC submentaa kaaren A⌒C: n d.

Sama kuva näyttää kulman ∠DOE, jota ei ole rekisteröity kehässä, koska sen kehä ei ole sen ympärysmitta, vaan keskellä tai keskellä tai keskustassa.

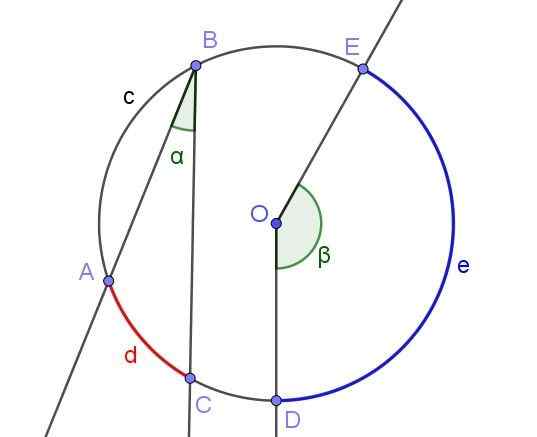Kuva 2. Rekisteröity kulma ∠ABC ja keskikulma ∠DOE. Lähde: f. Zapata geogebralla.

[TOC]

Keskikulma

Rekisteröidyn kulman lisäksi keskikulma, joka on se, jonka kärki on kehän keskellä ja joiden sivut leikataan kehään.

Voi palvella sinua: ero yhteisen osan ja desimaalin välillä

RADIANES -MITTAMINEN KÄSITTELY on osoitus kaaren välillä, joka on kulman sivujen välinen kaaren ja kehän säteen välinen kehyskaari ja kehän säde.

Jos ympärysmitta on yhtenäinen (säde 1), kaaren pituus samoissa radioyksiköissä on radianien kulman mittaus.

Ja kun kulman mitta vaaditaan asteina, mittaus kerrotaan radiaaneissa tekijällä 180º/π.

Kulmien mittauslaitteet käyttävät aina keskikulmaa ja kaaren pituutta, jonka tämä suoraan kalibroitu asteina. Tämä tarkoittaa, että aina kun kulma mitataan, mitattuna on keskikulman alistaman kaaren pituus.

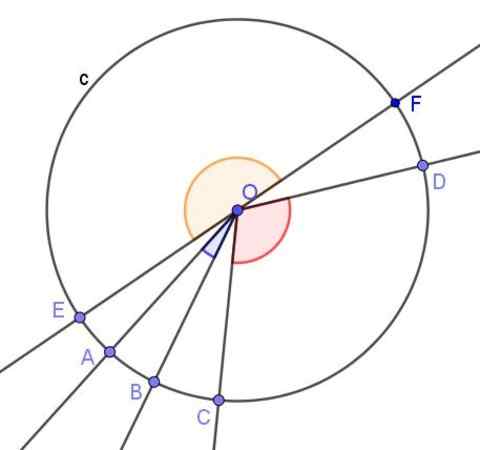Kuva 3. Useita kehän keskikulmia. Lähde: f. Zapata geogebralla.

Lauseet

- Lause 1 (rekisteröity kulma ja keskikulma)

Rekisteröidyn kulman mitta on puolet keskikulman mittauksesta, jos molemmat kulmat alaavat saman kaaren.

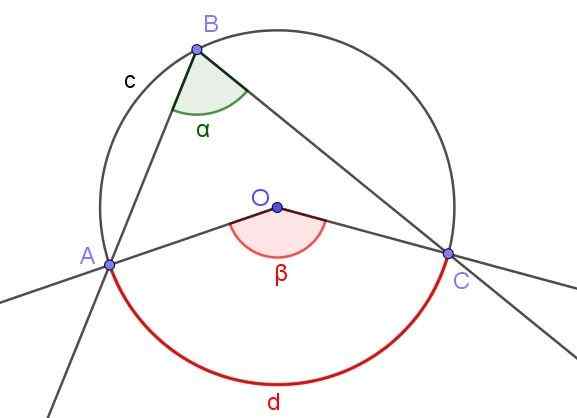Kuva 4. Rekisteröity kulma ∠ABC ja keskikulma ∠AOC, jotka alistavat saman kaaren A⌒C: n. Lähde: f. Zapata geogebralla.

Kuvio 4 esittää kaksi kulmaa ∠ABC ja ∠AOC, jotka leikkaavat saman kehän kaaren A⌒C.

Jos rekisteröidyn kulman mitta on α, niin keskikulman p -mitta on kaksinkertainen rekisteröidyn kulman mittaan (β = 2 α), koska molemmat vähentävät saman mitatun kaaren D.

Esittely 1

Lauseen 1 osoittamiseksi useita erityistapauksia alkaa, kunnes pääsee yleiseen tapaukseen.

Voi palvella sinua: Sandwich Law: Selitys ja harjoitukset

Oletetaan, että rekisteröity kulma, jossa yksi sen sivuista kulkee kehän keskikohdan läpi, kuten kuvassa 5 esitetään.

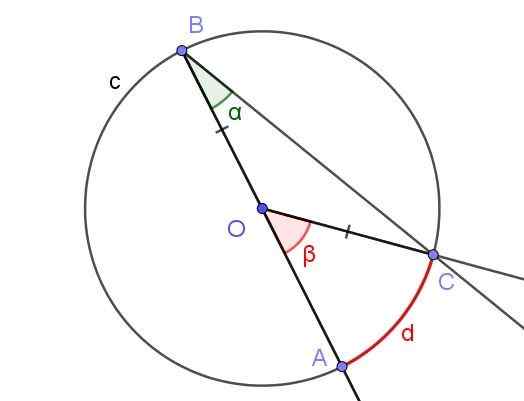Kuva 5. Rekisteröity kulma ∠ABC sivulla [BA) O: n ja keskikulman kautta ∠AOC. Lähde: f. Zapata geogebralla.

Tässä tapauksessa muodostuu COB -šosceles Triange, koska [OC] = [OB].

ISCELES -kolmiossa pohjan vieressä olevat kulmat ovat samat, siksi niiden on ∠BCO = ∠ABC = α. Toisaalta ∠COB = 180º - β.

Ottaen huomioon COB -kolmion sisäkulmien summa:

α + α + (180º - β) = 180º

Missä seuraa, että 2 α = β tai mikä on ekvivalentti: α = β/2. Tämä on samanaikainen lauseen 1 mukaan: rekisteröidyn kulman mitta on puolet keskikulmasta, jos molemmat kulmat toimittavat saman köyden [AC].

Esittely 1B

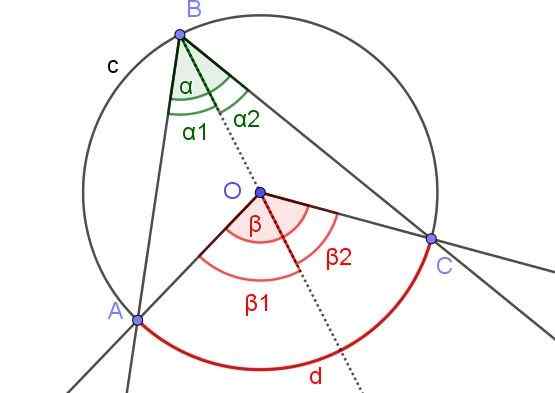Kuva 6. Apurakenne osoittamaan, että α = β/2. Lähde: f. Zapata geogebralla.

Tässä tapauksessa on kirjoitettu kulma ∠ABC, jossa keskusta tai kehä on kulman sisällä.

Lauseen 1 esittämiseksi tässä tapauksessa piirretään puolikielinen apulaite [BO), joten on olemassa kaksi rekisteröityä kulmaa ∠ABO: ta ja ∠OBC: tä mainitun puolijohdun vieressä.

Samoin heillä on keskuskulmat β₁ ja β₂ mainitun puolijuoteisen vieressä. Tällä tavalla sinulla on sama tilanne kuin demonstraatiossa 1, joten voidaan todeta, että α₂ = β₂ /2 ja α₁ = β₁ /2. Kuten α = α₁ + α₂ ja β = β₁ + β₂ Siksi on, että α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Voi palvella sinua: integraalit tyypit

Yhteenvetona α = β / 2, joka täyttää lauseen 1.

- Lause 2

Jos kaksi tai useampia rekisteröityjä kulmia Subtsen on sama kaari, niin heillä on sama mitta.

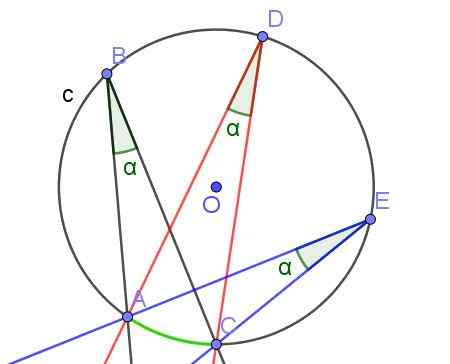Kuva 7. Rekisteröidyt kulmat, joiden mitta on yhtä suuri, koska ne subtsen saman kaaren A⌒C. Lähde: f. Zapata geogebralla.

- Lause 3

Rekisteröityjen kulmien tekstitys on sama mittaus, samat.

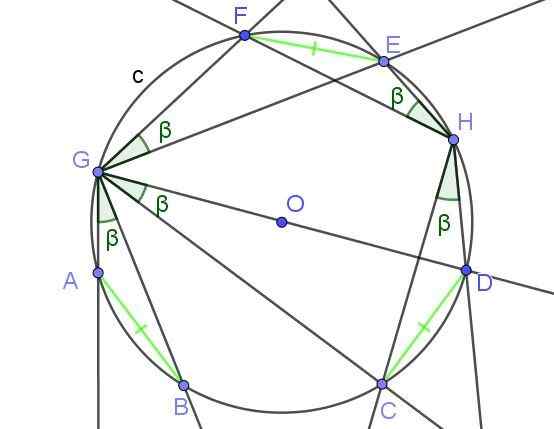Kuva 8. Kirjoitetuilla kulmilla, joilla subtus -köydet ovat yhtä suuret, on yhtä suuri mitta β. Lähde: f. Zapata geogebralla.

Esimerkit

- Esimerkki 1

Osoita, että kirjoitetut kulman alaosat Halkaisija on oikea kulma.

Ratkaisu

Halkaisijaan liittyvä keskuskulma ∠AOB on tasainen kulma, jonka mitta on 180º.

Lauseen 1 mukaan minkä tahansa kehän rekisteröidyn kulman, joka on saman köyden (tässä tapauksessa halkaisija), on mitattuna keskuskulman puoliksi, joka alistaa saman köyden, joka esimerkillemme on 180º/2 = 90º.

Kuva 9. Kaikki rekisteröidyt kulma, joka on halkaisija, on suorakulma. Lähde: f. Zapata geogebralla.

- Esimerkki 2

Linja (BC) -tangentti A: n kehä C: ssä määrittää kirjoitetun kulman ∠BAC (katso kuva 10).

Varmista, että rekisteröityjen kulmien lause 1 täyttyy.

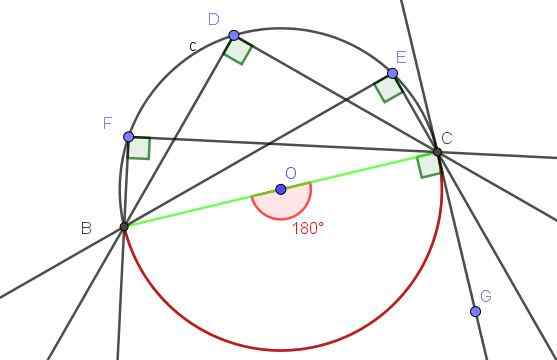
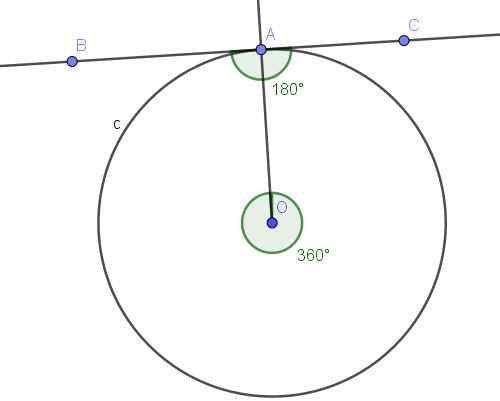Kuva 10. Rekisteröity kulma BAC ja sen kupera keskuskulma AOA. Lähde: f. Zapata geogebralla.

Ratkaisu

Kulma ∠BAC on rekisteröity, koska sen kärki on kehällä ja sen sivut [AB) ja [AC) ovat tangentteja kehälle, joten kirjoitetun kulman määritelmä täyttyy.

Toisaalta kirjoitettu kulma isterbac submentaa A⌒A -kaaria, joka on koko kehä. Keskuskulma, joka subtentoi A⌒A -kaaria, on kupera kulma, jonka mitta on koko kulma (360º).

Rekisteröity kulma alaosaa koko kaari mittaa puolet niihin liittyvästä keskikulmasta, ts. ∠BAC = 360º/2 = 180º.

Kaikkien edellä mainittujen kanssa on todistettu, että tämä tapaus täyttää lauseen 1.

Viitteet

1. Kalju. (1973). Geometria ja trigonometria. Keski -Amerikan kulttuuritoimitus.
2. JA. -Lla. (2003). Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
3. Geometria 1. Kulmat kehässä. Palautettu: Edu.Xunta.On/
4. Kaikki tieteet. Ehdotetut kulmaharjoitukset kehässä. Toipunut: Francesphysics.Blogin.com
5. Wikipedia. Rekisteröity kulma. Palautettu: on.Wikipedia.com