Ratkaistu ulkoiset vaihtoehtoiset kulmaharjoitukset ja harjoitukset

Se Ulkoiset vaihtoehtoiset kulmat Ne ovat kulmia, jotka muodostuvat, kun kaksi yhdensuuntaista viivaa siepataan kuivausviivan kanssa. Näiden kulmien lisäksi muodostuu toinen vääntömomentti, jota kutsutaan sisäisiksi vaihtoehtoisiksi kulmiiksi.

Ero näiden kahden käsitteen välillä on "ulkoiset" ja "sisäiset" sanat ja kuten nimi on osoitettu, ulkoiset vaihtoehtoiset kulmat ovat ne, jotka muodostuvat kahden yhdensuuntaisen viivan ulkopuolelle.

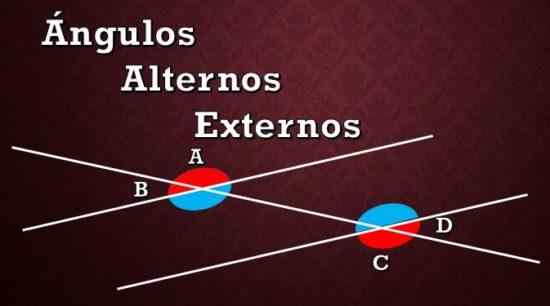
Vaihtoehtoisten ulkoisten kulmien a, b ja c, d graafinen esitys

Kuten edellisessä kuvassa voidaan nähdä, kahden yhdensuuntaisen viivan ja kuivauslinjan väliin on muodostettu kahdeksan kulmaa. Punaiset kulmat ovat ulkoisia vaihtoehtoisia, ja siniset kulmat ovat sisäiset vaihtoehtoiset kulmat.

[TOC]

Ulkoisten vaihtoehtoisten kulmien ominaisuudet

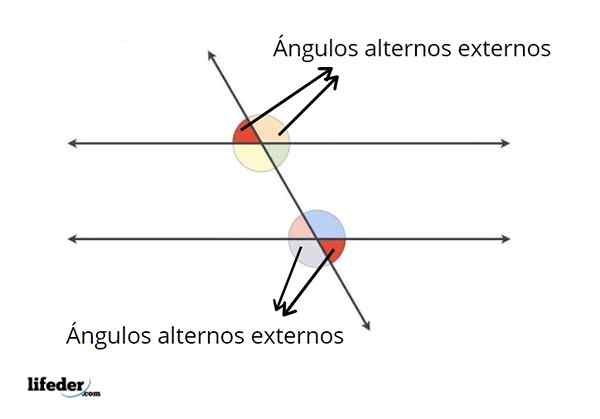Esimerkkejä ulkoisista vaihtoehtoisista kulmista

Johdannossa jo selitettiin, mitkä ulkoiset vaihtoehtoiset kulmat ovat. Sen lisäksi, että nämä kulmat ovat samankaltaisten ulkoisten kulmien välillä, ne täyttävät toisen tilan.

Heidän täytäntöönpano on, että rinnakkaislinjalle muodostuvat ulkoiset vaihtoehtoiset kulmat ovat yhdenmukaisia; Sillä on sama mitta kuin kahdella muulla, jotka muodostuvat toiselle rinnakkaisviivalle.

Mutta jokainen ulkoinen vaihtoehtoinen kulma on yhdenmukainen Secant -viivan toisella puolella olevaan kanssa.

Mitkä ovat yhdenmukaiset ulkoiset vaihtoehtoiset kulmat?

Jos havaitaan alun kuva ja aikaisempi selitys, voidaan päätellä, että toistensa kanssa yhdenmukaiset ulkoiset vaihtoehtoiset näkökulmat ovat: kulmat A ja C ja kulmat B ja D.

Osoittaa, että he ovat yhdenmukaisia.

Voi palvella sinua: Jatkuva toiminta: Ominaisuudet, esimerkit, harjoitukset

Ratkaisut

Alla on sarja harjoituksia, joissa on sovellettava ulkoisten vaihtoehtoisten kulmien määritelmä ja omaisuus.

Ensimmäinen harjoitus

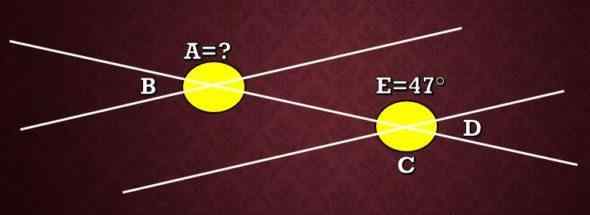
Seuraavassa kuvassa mikä on kulman A mittari, että kulma E mittaa 47 °?

Ratkaisu

Kuten aiemmin selitetään, kulmat A ja C ovat yhteneviä ulkoisen vaihtoehtoisen suhteen. Siksi A: n mitta on yhtä suuri kuin C: n mitta. Nyt, koska kulmat E ja C ovat vastakkaisia ​​kulmia kärkipisteellä, heillä on, että niillä on sama mitta, siksi C: n mitta on 47 °.

Yhteenvetona voidaan todeta, että mitta on yhtä suuri kuin 47 °.

Toinen harjoitus

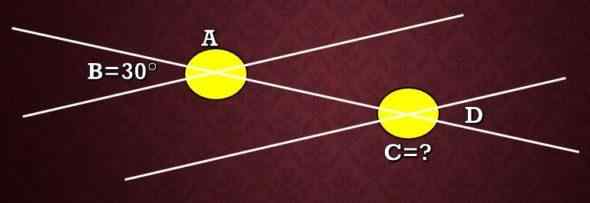
Laske seuraavassa kuvassa esitetyn kulman C mitta, tietäen, että kulma B mittaa 30 °.

Ratkaisu

Tässä esimerkissä määritelmää käytetään. Kaksi kulmaa ovat täydentäviä, jos niiden mittaus on yhtä suuri kuin 180 °.

Kuvassa voidaan nähdä, että a ja b ovat lisäyksiä, joten A+B = 180 °, ts.+30 ° = 180 ° ja siksi A = 150 °. Nyt, kuten A ja C, ne ovat ulkoisia vaihtoehtoisia kulmia, joten sen mitat ovat samat. Siksi C -mitta on 150 °.

Kolmas harjoitus

Seuraavassa kuvassa kulman A mitta on 145 °. Mikä on kulman E mitta?

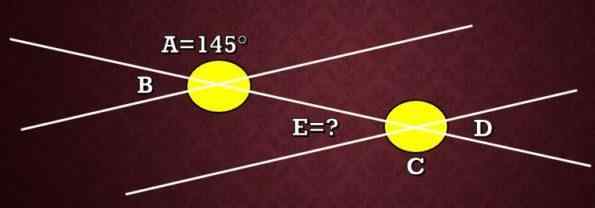
Ratkaisu

Kuvassa voidaan nähdä, että kulmat A ja C ovat ulkoisia vaihtoehtoisia kulmia, siksi niillä on sama mitta. Toisin sanoen C: n mitta on 145 °.

Koska kulmat C ja E ovat lisäkulmia, sen on oltava C+E = 180 °, eli 145 °+E = 180 ° ja siksi kulman E mita on 35 °.

Voi palvella sinua: näytteenottovirhe: kaavat ja yhtälöt, laskenta, esimerkit

Viitteet

1. Bourke. (2007). Kulma geometrian matematiikan työkirja. NewPath Learning.
2. C. JA. -Lla. (2003). Geometriaelementit: lukuisilla harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
3. Clemens, S. R -., O'Dafer, P. G., & Cooney, T. J -. (1998). Geometria. Pearson -koulutus.
4. Lang, s., & Murrow, G. (1988). Geometria: Lukiokurssi. Springer Science & Business Media.
5. Lira, a., Jaime, P., Chavez, m., Gallegos, m., & Rodríguez, c. (2006). Geometria ja trigonometria. Umbral Editions.
6. Moyano, a. R -., Saro, a. R -., & Ruiz, R. M. (2007). Algebra ja neliöinen geometria. Netbiblo.
7. Palmer, c. Yllyttää., & Bibb, S. F. (1979). Käytännön matematiikka: aritmeettinen, algebra, geometria, trigonometria ja laskentasääntö. Palautus.
8. Sullivan, M. (1997). Trigonometria ja analyyttinen geometria. Pearson -koulutus.
9. Wingard-Enelson, R. (2012). Geometria. ENLLOW Publishers, Inc.