Vektorin suorakulmaiset komponentit (harjoituksilla)

Se vektorin suorakulmaiset komponentit ovat tietoja, jotka muodostavat tämän vektorin. Niiden määrittämiseksi on välttämätöntä olla koordinaattijärjestelmä, joka on yleensä Cartesian lentokone.

Kun koordinaattijärjestelmässä on vektori, sen komponentit voidaan laskea. Nämä ovat 2, vaakasuora komponentti (yhdensuuntainen x -akselin kanssa), nimeltään ”X -akselin komponentti” ja pystysuuntainen komponentti (yhdensuuntainen Y -akselin kanssa), nimeltään ”komponentti Y -akselissa” ””.

Vektorin suorakulmaisten komponenttien graafinen esitys

Komponenttien määrittämiseksi se on välttämätöntä.

[TOC]

Kuinka määrittää vektorin suorakulmaiset komponentit?

Näiden komponenttien määrittämiseksi tietyt suorakulmioiden ja trigonometristen toimintojen väliset suhteet on tiedettävä.

Seuraavassa kuvassa voit nähdä tämän suhteen.

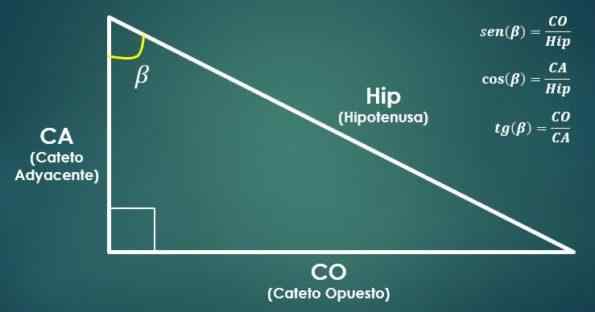Suorakulmioiden ja trigonometristen toimintojen väliset suhteet

Kulman rinta on yhtä suuri kuin Cateton mittauksen välinen osamäärä ja hypotenusen mitta ja mittaus.

Toisaalta kulman kosiini on yhtä suuri kuin osamäärä Cateton mittauksen välillä kulman vieressä ja hypotenusen mittana.

Kulman tangentti on yhtä suuri kuin vastakkaisen jalan mitan ja viereisen Catoton mittaus.

Kaikissa näissä suhteissa on välttämätöntä määrittää vastaava suorakulmio kolmio.

Onko muita menetelmiä?

Joo. Annetuista tiedoista riippuen tapa laskea vektorin suorakulmaiset komponentit voivat vaihdella. Toinen työkalu, jota käytetään paljon, on Pythagoras -lause.

Voi palvella sinua: olemassaolo ja ainutlaatuisuus lause: esittely, esimerkit ja harjoitukset

Ratkaisut

Seuraavat harjoitukset toteuttivat käytännössä vektorin suorakulmaisten komponenttien ja yllä kuvattujen suhteiden määritelmän.

Ensimmäinen harjoitus

On tiedossa, että vektori A: n suuruus on yhtä suuri kuin 12 ja kulmassa, jonka tällä muodossa X -akselilla on 30 °. Määritä mainitun vektorin suorakulmaiset komponentit.

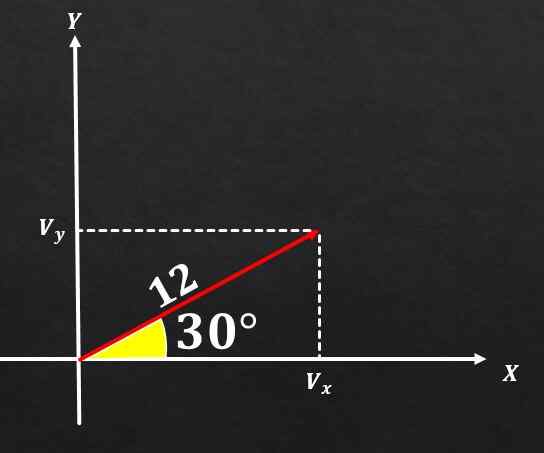
Ratkaisu

Jos kuvaa arvostetaan ja yllä kuvattua kaavoja käytetään, voidaan päätellä, että komponentti ja vektori A on yhtä suuri kuin

sin (30 °) = vy / 12, ja siksi vy = 12*(1/2) = 6.

Toisaalta vektorin A x -akselin komponentti on yhtä suuri kuin

cos (30 °) = vx / 12 ja siksi vx = 12*(√3 / 2) = 6√3.

Toinen harjoitus

Jos vektori A: n suuruus on yhtä suuri kuin 5 ja X -akselin komponentti on yhtä suuri kuin 4, määritä A -akselin A -komponentin arvo.

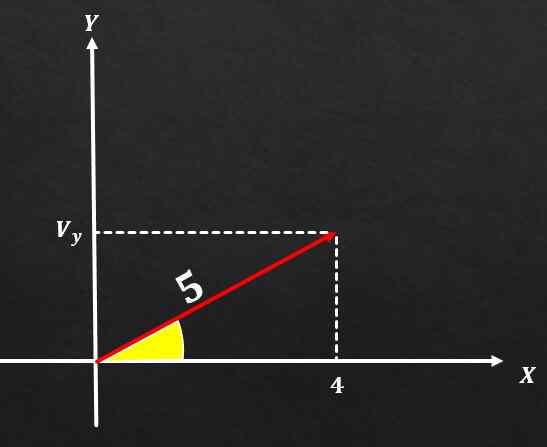
Ratkaisu

Pythagoras -lauseen avulla vektorin suuruuden suuren neliön on oltava yhtä suuri kuin kahden suorakulmaisen komponentin neliöiden summa. Eli m² = (vx) ² + (vy) ².

Korvataan tarjotut arvot, sinun on

5² = (4) ² + (VY) ², siksi 25 = 16 + (VY) ².

Tämä tarkoittaa, että (vy) ² = 9 ja siten vy = 3.

Kolmas harjoitus

Jos vektori A: n voimakkuus on yhtä suuri kuin 4 ja tämä muodostaa kulman 45 ° X -akselin kanssa, määritä mainitun vektorin suorakulmaiset komponentit.

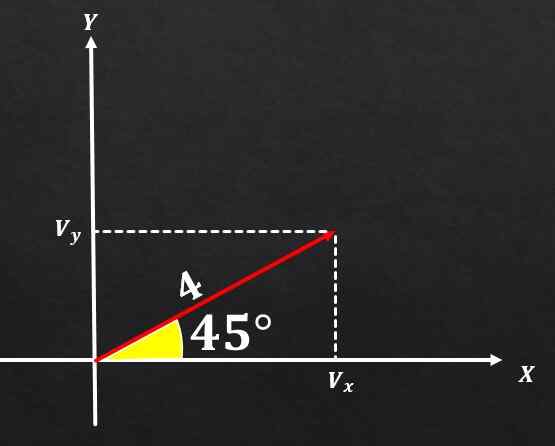
Ratkaisu

Käyttämällä suorakulmion kolmion ja trigonometristen funktioiden välisiä suhteita voidaan päätellä, että komponentti ja vektori A on yhtä suuri kuin

sin (45 °) = vy / 4 ja siksi vy = 4*(√2 / 2) = 2√2.

Toisaalta vektorin A x -akselin komponentti on yhtä suuri kuin

Voi palvella sinua: yhdistetty peräkkäin

cos (45 °) = vx / 4 ja siksi vx = 4*(√2 / 2) = 2√2.

Viitteet

1. Landaverde, f. D -d. (1997). Geometria (Uusintapainos ED.-A. Edistyminen.
2. Leake, D. (2006). Kolmiot (Kuvitettu ED.-A. Heinemann-raintree.
3. Pérez, c. D -d. (2006). Ennakkoluulo. Pearson -koulutus.
4. Ruiz, á., & Barrantes, H. (2006). Geometriat. CR -teknologinen.
5. Sullivan, M. (1997). Ennakkoluulo. Pearson -koulutus.
6. Sullivan, M. (1997). Trigonometria ja analyyttinen geometria. Pearson -koulutus.