Täydentävät kulmat, jotka ja miten lasketaan, esimerkkejä, harjoituksia

Kaksi tai useampaa kulmaa on täydentävät kulmat Jos sen mittojen summa vastaa suorakulmaa. Kuten tiedetään, oikean kulman mitta asteina on 90º, ja radianeissa se on π/2.

Esimerkiksi suorakulmion kolmion hypoteenin vieressä olevat kaksi kulmaa ovat toisiaan täydentäviä, koska niiden mitat ovat 90º. Seuraava luku on siitä erittäin havainnollistava:

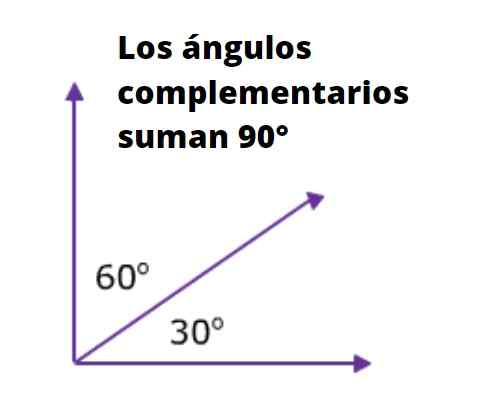
Kuvio 1. Vasemmalla puolella useita kulmia, joissa on yhteinen kärki. Oikealla kulma 60º, joka täydentää kulmaa α (alfa). Lähde: f. Zapata.

Kuvio 1 esittää yhteensä neljä kulmaa. α ja β ovat täydentäviä, koska ne ovat viereinen ja sen täydellinen summa suorassa kulmassa. Samoin β on komplementaarinen kuin y, missä seuraa, että y ja α ovat yhtä suuret.

Nyt, koska a ja δ on yhtä suuri kuin 90 astetta, voidaan sanoa, että a ja δ ovat täydentäviä. Lisäksi, koska β: lla ja δ: llä on sama komplementaarinen a, voidaan sanoa, että β: lla ja δ: llä on sama mitta.

 [TOC]

Esimerkkejä täydentävistä kulmista

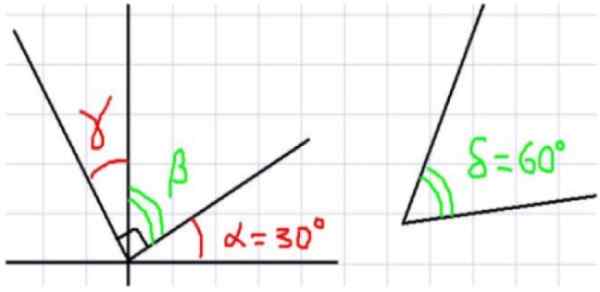
Seuraavissa esimerkeissä pyydetään löytämään tuntemattomat kulmat, jotka on merkitty kuulustelulla kuvassa 2.

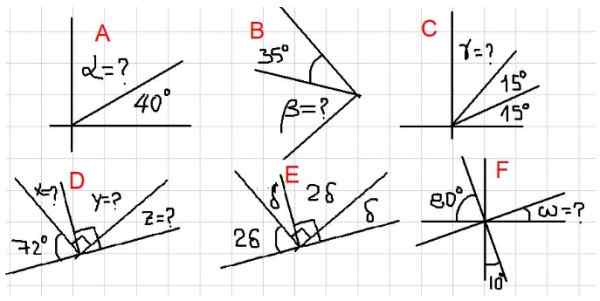Kuva 2. Erilaisia ​​esimerkkejä täydentävistä kulmista. Lähde: f. Zapata.

- Esimerkkejä A, B ja C

Seuraavat esimerkit ovat monimutkaisuuden järjestystä.

Esimerkki a

Yläkuviossa meillä on, että viereiset kulmat α ja 40º lisäävät suorakulmaan. Eli α + 40º = 90º, siksi α = 90º- 40º = 50º.

Esimerkki b

Koska β on komplementaarinen 35º: n kulman kanssa, sitten β = 90º - 35º = 55º.

Voi palvella sinua: Orthoedro: kaavat, alue, tilavuus, diagonaali, esimerkkejä

Esimerkki C

Kuviosta 2C, γ + 15º + 15º = 90º: n summa. Toisin sanoen γ on komplementaarinen kulmalle 30 = 15º + 15º. Jotta:

γ = 90º- 30º = 60º

- Esimerkkejä d, e ja f

Näissä esimerkeissä mukana on enemmän kulmia. Tuntemattomien löytämiseksi lukijan on sovellettava täydentävän kulman käsitettä niin monta kertaa kuin tarpeen.

Esimerkki D

Koska x on täydentävä 72º: n kanssa, seuraa, että x = 90º - 72º = 18º. Lisäksi ja se on täydentävä x, sitten Y = 90º - 18º = 72º.

Lopuksi z on täydentävä ja. Kaikista edellä mainituista seuraa: että:

Z = 90º - 72º = 18º

Esimerkki E

Kulmat δ ja 2δ ovat komplementaarisia, siksi Δ + 2δ = 90º.

Eli 3A = 90º, mikä tarkoittaa, että δ = 90º / 3 = 30º.

Esimerkki f

Jos kutsumme ω: n ja 10: n välistä kulmaa, sitä oli täydennettävä heille, koska havaitaan, että niiden täydellinen summa suorassa kulmassa. Missä seuraa, että u = 80º. Koska u on täydentävä ω, sitten ω = 10º.

Harjoitukset

Seuraavassa ehdotetaan kolme harjoitusta. Kaikissa niissä kulmien A ja B arvo on löydettävä asteina siten, että kuviossa 3 esitetyt suhteet täyttyvät.

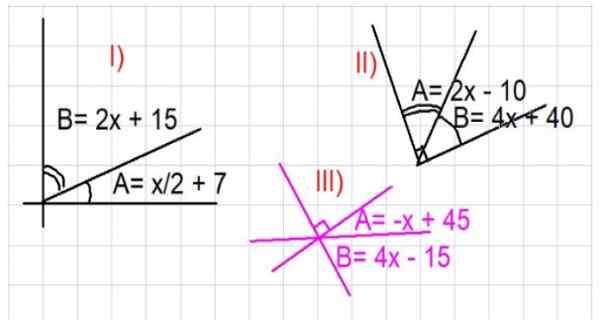Kuva 3. Kuvia täydentäviä kulmaharjoituksia. Lähde: f. Zapata.

- Harjoitus 1

Määritä kuvan 3 osan A ja B arvot).

Ratkaisu

Kuviosta nähdään, että a ja b ovat täydentäviä, siksi A + B = 90º. A: n ja B: n lauseke korvataan osassa I) funktiona):

Voi palvella sinua: lähentymisradio: Määritelmä, esimerkit ja harjoitukset ratkaistu

(x/2 + 7) + (2x + 15) = 90

Sitten termit on ryhmitelty oikein ja saadaan yksinkertainen lineaarinen yhtälö:

(5x/2) + 22 = 90

22 vähentäminen molemmissa jäsenissä on:

5x/2 = 90 -22 = 68

Ja lopuksi x: n arvo tyhjennetään:

x = 2*68/5 = 136/5

Nyt kulma löytyy korvaavan x: n arvon:

A = (136/5)/2 +7 = 103/5 = 20,6 º.

Kun taas kulma B on:

B = 2*136/5 + 15 = 347/5º = 69,4º .

- Harjoitus 2

Etsi kuvan II kulmien A ja B arvot, kuva 3.

Ratkaisu

Jälleen, kun A ja B ovat täydentäviä kulmia, sinun on: A + B = 90º. A: n ja B: n ekspression korvaaminen osassa II) 3 funktiona on:

(2x - 10) + (4x +40) = 90

Samanlaiset termit on ryhmitelty yhtälön saamiseksi:

6 x + 30 = 90

Molempien jäsenten jakaminen 6: n välillä saadaan:

x + 5 = 15

Missä se seuraa, että x = 10º.

Siksi:

A = 2*10 - 10 = 10º

B = 4*10 + 40 = 80º.

- Harjoitus 3

Määritä kuvan 3 osan A ja B arvot) arvot 3.

Ratkaisu

Kuva analysoidaan huolellisesti täydentävien kulmien etsimiseksi. Tässä tapauksessa sinun on + b = 90 astetta. A- ja B: n lausekkeen korvaaminen kuvassa annetun x: n funktiona, sinulla on:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Molempien jäsenten jakaminen 3: lla on seuraava:

x + 10 = 30

Missä se seuraa, että x = 20º.

Toisin sanoen kulma A = -20 +45 = 25º. Ja sen puolesta: b = 4*20 -15 = 65º.

Kohtisuorassa sivukulmat

Sanotaan, että kaksi kulmaa on kohtisuora Jos kummallakin puolella on vastaava kohtisuorassa toisessa. Seuraava luku selventää käsitettä:

Voi palvella sinua: yhdistetty peräkkäin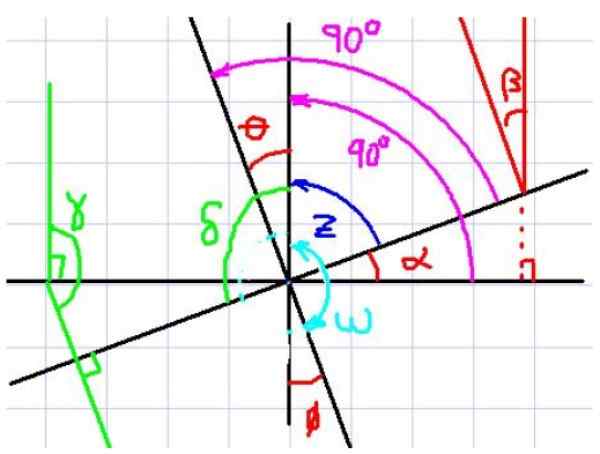Kuva 4. Kohtisuorassa sivukulmat. Lähde: f. Zapata.

Kuviossa 4 havaitaan kulmia α ja θ, esimerkiksi. Huomaa nyt, että jokaisella kulmalla on vastaava kohtisuorassa toisessa kulmassa.

On myös nähtävissä, että α: lla ja θ: lla on sama täydentävä kulma z -z, Siksi tarkkailija päättelee välittömästi, että α ja θ on sama mitta. Näyttää siltä, ​​että jos kahdella kulmalla on kohtisuorassa puolet toistensa kanssa, ne ovat samat, mutta katsotaanpa toinen tapaus.

Harkitse nyt kulmia α ja ω. Näillä kahdella kulmalla on myös vastaavat kohtisuorat puolet, mutta ei voida sanoa, että ne ovat yhtä suuret, koska toinen on akuutti ja toinen on sotkuinen.

Huomaa, että ω + θ = 180º. Lisäksi θ = α. Jos vaihdat tämän z: n lausekkeen ensimmäisessä yhtälössä, jonka saat:

Δ + α = 180º, että Δ ja α ovat molemminpuolisesti kohtisuorien puolten kulmia.

Yleinen sääntö kohtisuoralle sivukulmalle 

Edellä mainituista sääntö, joka on aina täytetty, että kulmilla on kohtisuora puolet:

Jos kaksi kulmaa ovat molemminpuolisesti kohtisuorassa, niin ne ovat samat, jos molemmat ovat akuutteja tai molemmat ovat sotkuisia. Muutoin, jos yksi on akuutti ja toinen on sotkuinen, niin ne ovat täydentäviä, ts. Ne lisäävät 180º.

Tämän säännön soveltaminen ja kuvan 4 kulmiin voimme vahvistaa seuraavat:

α = β = θ = φ

γ = δ

Α: n, β: n, θ: n ja φ: n lisäkulman kanssa.

Viitteet

1. Baldor, J. -Lla. 1973. Litteä ja avaruusgeometria. Keski -Amerikan kulttuuri-. 
2. Matemaattiset lait ja kaavat. Kulman mittausjärjestelmät. Haettu: Ingemecanica.com.
3. Wentworth, G. Planeetan geometria. Toipunut: Gutenberg.org.
4. Wikipedia. Täydentävät kulmat. Palautettu: on.Wikipedia.com
5. Wikipedia. Kuljettaja. Palautettu: on.Wikipedia.com
6. Zapata f. Goniometri: Historia, osat, toiminta. Haettu: Lifer.com