Keski -symmetriaominaisuudet, esimerkit ja harjoitukset

Kaksi pistettä A ja 'on keskeinen symmetria kohdasta tai kun AA -segmentti "kulkee sen läpi ja on myös AA: n keskipiste '. Kohtaan tai kutsutaan Symmetriakeskus.

ABC -kolmion keskeinen symmetrinen suhteessa yhteen pisteeseen tai on toinen kolmio a'b'c ', jolla on seuraavat ominaisuudet:

-Homologiset segmentit ovat yhtä pituisia 

-Niiden vastaavilla kulmilla on sama mitta.

Kuvio 1. ABC -kolmio ja sen symmetrinen A'b'c '. Lähde: f. Zapata.

Kuviossa 1 ABC -kolmio (punainen) ja sen keskeinen symmetrinen A'b'c '(vihreä) suhteessa symmetrian keskipisteeseen tai. 

Samassa luvussa tarkkaavainen tarkkailija ymmärtäisi, että sama tulos saadaan soveltamalla alkuperäistä kolmion kiertoa, kunhan se on 180º ja keskittynyt tai keskittynyt tai.

Siksi keskeinen symmetria vastaa 180º käännöstä suhteessa symmetriakeskukseen.

[TOC]

Keskeisen symmetrian ominaisuudet

Keskeisellä symmetrialla on seuraavat ominaisuudet:

-Symmetriakeskus on segmentin keskipiste, joka liittyy pisteeseen sen symmetrisellä.

-Toisen symmetrinen piste, joka sijaitsee symmetriakeskuksessa, tapahtuu samanaikaisesti symmetrian keskustan kanssa.

-Kolmion keskeinen symmetrinen on yhdenmukainen kolmio (yhtä suuri) alkuperäisen kanssa.

-Kuva kehän keskussymmetria on toinen yhtäläisen säteen ympärysmitta.

-Ympyrällä on keskeinen symmetria omaan keskukseen.

Kuva 2. Suunnittelu keskeisellä symmetrialla. Lähde: Pixabay.

-Ellipsellä on keskeinen symmetria sen keskuksen suhteen.

-Segmentissä on keskeinen symmetria sen keskipisteeseen nähden.

-Tasasivuisella kolmiolla ei ole keskussymmetriaa sen keskustaan ​​nähden, koska sen symmetrinen, vaikka se on yhdenmukainen ensimmäiselle, antaa tasasivuisen kolmion käännöksen.

Se voi palvella sinua: y = 3Sen (4x) toimintojakso

-Neliöillä on keskeinen symmetria keskuksensa suhteen.

-Pentagonista puuttuu keskeinen symmetria sen keskuksen suhteen.

-Tavallisilla monikulmioilla on keskussymmetria, kun heillä on useita vääntömomenttipuolia.

Esimerkit

Symmetriakriteereillä on monia sovelluksia tieteessä ja tekniikassa. Keskeistä symmetriaa on luonteeltaan, esimerkiksi jääkiteillä ja hämähäkinverhoilla on tällainen symmetria.

Lisäksi monia ongelmia ratkaistaan ​​helposti, kun käytetään keskussymmetrian ja muun tyyppistä symmetriaa. Siksi on kätevää tunnistaa nopeasti, kun se tapahtuu.

Kuva 3. Jääkiteillä on keskussymmetria. Lähde: Pixabay.

Esimerkki 1

Kun koordinaattien (a, b) on pisteen P, sinun on löydettävä sen symmetrisen P 'koordinaatit alkuperästä tai koordinaateista (0, 0).

Ensimmäinen asia on rakentaa p 'p', jolle piirretään viiva, joka kulkee alkuperän tai pisteen P läpi. Tämän viivan yhtälö on y = (b/a) x.

Kutsutaan nyt (A ', B') symmetrisen pisteen koordinaatit P '. Piste P. Lisäksi OP -etäisyyden on oltava yhtä suuri kuin OP ', joka kirjoittaa analyyttisesti näin:

√ (a² + b -²) = √ (a '² + B '² -A

Seuraava on korvata b '= [(b/a).A '] edellisessä lausekkeessa ja neliössä tasa -arvon molemmilla puolilla neliöjuuren poistamiseksi: (a² + b -²) = [a '² + (b²/²-A.to '²-

Uuttamalla yleinen tekijä ja yksinkertaistamalla, se saavutetaan '² = a². Tällä yhtälöllä on kaksi todellista ratkaisua: a '= +a tai' = -a. 

Saadaksesi b ', käytämme uudelleen b' = (b/a) a '. Jos A: n positiivinen ratkaisu korvataan, saavutetaan, että b '= B. Ja kun negatiivinen ratkaisu korvataan, niin b '= -b. 

Voi palvella sinua: mitkä ovat kehän 7 elementtiä?

Positiivinen ratkaisu antaa P ': lle samalle pisteelle P, joten se suljetaan pois. Negatiivinen ratkaisu tarjoaa ehdottomasti symmetrisen pisteen koordinaatit:

P ': (-a, -b)

Esimerkki 2

On osoitettava, että AB -segmentti ja sen symmetrinen keskus A'B 'on sama pituus.

Alkaen kohdan A koordinaateista, jotka ovat (kirves, ay) ja pisteen B: (bx, kirjoittanut), AB: n pituus on antanut:

D (ab) = √ ((bx - kirves)² + (Kirjoittanut - ay)² -A

Analogialla symmetrisellä segmentillä A'B 'on annettu:

d (a'b ') = √ ((bx' - ax ')² + (Kirjoittanut ' - ay')² -A

Symmetrisen pisteen a '' ovat ax '= -ax ja ay' = -ay koordinaatit. Samoin b 'ovat bx' = -bx ja '= -by. Jos nämä koordinaatit korvataan etäisyyden D (a'b ') yhtälössä, sinulla on:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) se vastaa:

 √ ((bx - kirves)² + (Kirjoittanut - ay)²) = D (AB)

Osoitetaan, että molemmilla segmenteillä on sama pituus.

Ratkaisut

- Harjoitus 1

Osoita analyyttisesti, että keskeinen symmetrinen tai säteen R ja keskusta tai, sama alkuperäinen ympärysmitta.

Ratkaisu

Säteen R ja keskiympyrän (0,0) yhtälö on:

x² + ja² = R² (Ympäristöyhtälö C)

Jos kehän jokaisessa kohdassa P ja koordinaatit (x, y) sen symmetrinen koordinaatti p ') löytyy, symmetrisen ympärysmitan yhtälö on:

x '² + ja'² = R² (Symmetrinen ympärysyhtälö C ')

Nyt viitataan esimerkin 1 tulokseen, joka päättelee, että pisteen P 'koordinaatit, symmetriset P: lle ja koordinaateille (A, B), on (-a, -b). 

Mutta tässä harjoituksessa pistellä P on koordinaatit (x, y), joten sen symmetrisellä P: llä on koordinaatit x '= -x e y' = -y. Tämän korvaaminen symmetrisessä ympärysyhtälössä on:

Voi palvella sinua: Rhomboid: Ominaisuudet, kuinka kehä ja alue vie pois

(-X)² + (-ja)² = R²

Joka vastaa: x²+ ja² = R², Johtopäätöksenä, että ympyrän keskussymmetrinen suhteessa sen keskustaan ​​on itse kehys.

- Harjoitus 2

Osoita geometrisellä tavalla, että keskussymmetria säilyttää kulmat.

Ratkaisu

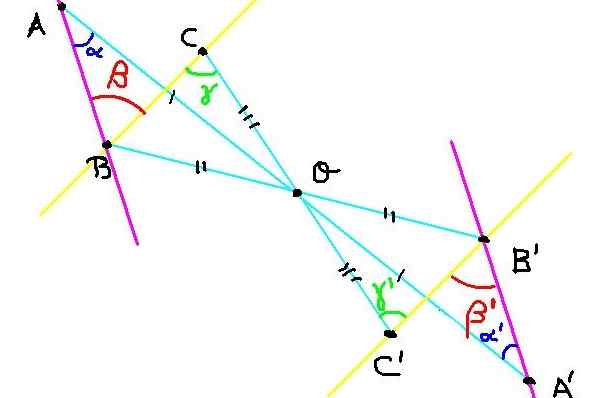Kuva 4. Symmetristen pisteiden rakentaminen harjoitukselle 2. Lähde: f. Zapata.

Koneessa on kolme pistettä A, B ja C. Sen symmetrinen A ', B' ja C 'on rakennettu suhteessa symmetriakeskukseen tai, kuten kuvassa 4 esitetään. 

Nyt meidän on osoitettava, että kulmalla ∡abc = β on sama mitta kuin kulmalla ∡a'b'c '= β' '.

Kuten c ja c 'ovat symmetrisiä, sitten OC = OC'. Samoin ob = ob 'y oa = oa'. Toisaalta kulma ∡boc = ∡b'oc 'vastustaa kärkipistettä.

Sitten kolmiot boc ja b'oc 'ovat yhdenmukaisia ​​siitä, että kahden puolen välillä on sama kulma yhtä suuri.

Koska boc on yhdenmukainen b'ocille ', niin kulmat  γ ja γ ' Ne ovat tasa -arvoisia. Mutta nämä näkökulmat täyttymisen lisäksi γ = γ ' Ne ovat sisäisiä vaihtoehtoisia BC- ja B'C '-linjojen välillä, mikä tarkoittaa, että BC -viiva on yhdensuuntainen B'C: n kanssa'.

Samoin BAA on yhdenmukainen siihen, mitä seuraa sitä α = α ' . Mutta  α ja α ' Ne ovat sisäisiä vaihtoehtoisia kulmia BA: n ja B'a '-linjojen välillä, joista päätellään, että linja BA on yhdensuuntainen B'A: n kanssa'.

Koska kulmassa ∡ABC = β on yhdensuuntainen sivu kulmassa ∡a'b'c '= β' ja myös molemmat ovat akuutteja, päätellään, että:

∡ABC = ∡A'B'C '= β = β' '

Tällä tavalla osoittaen, että keskussymmetria säilyttää kulmien mittauksen.

Viitteet

1. Baldor, J. -Lla. 1973.Litteä ja avaruusgeometria. Keski -Amerikan kulttuuri-. 
2. Matemaattiset lait ja kaavat. Kulman mittausjärjestelmät. Haettu: Ingemecanica.com.
3. Wentworth, G. Planeetan geometria. Toipunut: Gutenberg.org.
4. Wikipedia. Keskeinen symmetria. Palautettu: on.Wikipedia.com
5. Wikipedia. Kuljettaja. Palautettu: on.Wikipedia.com
6. Zapata f. Sisäiset ja ulkoiset konjugaattikulmat. Haettu: Lifer.com