Kulmat ympärysmittatyyppeissä, ominaisuuksissa, harjoituksissa ratkaistu

Nimeltään Ympäryskulmat niille, joissa mikä tahansa sen elementti on tai leikkaa tietyllä kehällä. Heidän joukossaan ovat seuraavat:

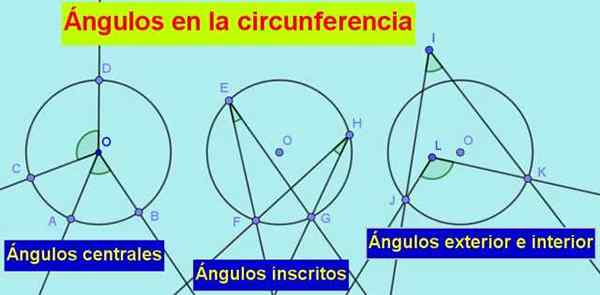
1.- Hän keskikulma, jonka kärkipiste on kehän keskellä ja sen sivut kuivuvat siihen, kuten seuraavassa kuvassa näemme:

Kuvio 1. Ympyrän tyypit ovat: keskeinen, kirjoitettu, ulkopinta ja sisä. Lähde: f. Zapata.

2.- Hän rekisteröity kulma, jonka kärkipiste on kehällä ja sen sivut ovat kuivia tai tangentteja kehälle.

3.- Ulkokulma, jonka kärkipiste on kehän ulkopuolella, mutta sen sivut ovat kuivat tai tangentti kehälle.

4.- Hän Sisäkulma, Kärkillä kehän sisällä ja sen kuivat sivut samaan.

Kaikki nämä näkökulmat pitävät tiettyjä suhteita toisiinsa ja tämä johtaa meidät tärkeisiin ominaisuuksiin tiettyyn ympärysmittaan kuuluvien kulmien välillä.

[TOC]

Ominaisuudet

- Keskikulma

Keskuskulma määritellään sellaiseksi, jonka kärki on kehän keskellä ja sen sivut leikataan kehään.

RADIANES -MITTAMINEN KÄSITTELY on osoitus kaaren välillä, joka on kulman sivujen välinen kaaren ja kehän säteen välinen kehyskaari ja kehän säde. 

Jos ympärysmitta on yhtenäinen, ts. Säde 1, niin keskikulman mitta on kaaren pituus, joka vastaa radiaanien lukumäärää.

Jos haluat keskikulman mittaa asteina, mittaus kerrotaan radiaaneissa tekijällä 180º/π.

Kulmien mittauslaitteet, kuten kuljettaja ja goniometri, käyttävät aina keskikulmaa ja alaosan pituutta.

Voi palvella sinua: Osittaiset johdannaiset: Ominaisuudet, laskelmat, harjoitukset

Ne kalibroidaan seksuaalisesti, mikä tarkoittaa, että aina kun kulma mitataan heidän kanssaan, mitattuna on kaaren pituus, jota keskikulma on aliarvioitu.

Omaisuus

Radianien keskikulman mitta on yhtä suuri kuin kaaren pituus, joka subtiinit tai sieppaukset jaettuna säteen pituudella.

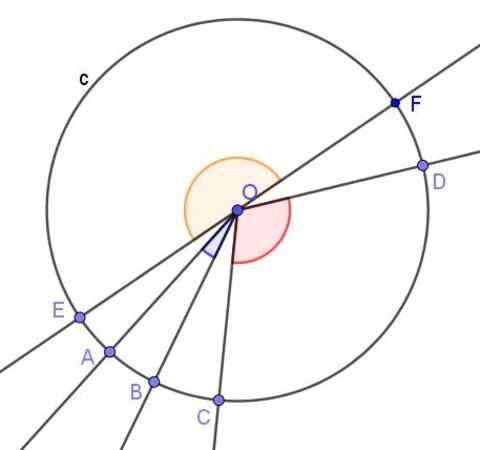Kuva 2. Kolme keskikulmaa on esitetty. Yksi akuutti, toinen tylsä ​​ja yksi tasainen. Lähde: f. Zapata.

- Rekisteröity kulma

Ympyrän rekisteröity kulma on sellainen, jolla on ympärysmitta ja sen puoliksi. 

Sen ominaisuudet ovat:

Ominaisuudet

-Rekisteröity kulma on kupera tai tasainen.

-Kun kirjoitettu kulma sieppaa saman kaaren kuin keskuskulma, ensimmäisen mita on puolet toisen mittauksesta.

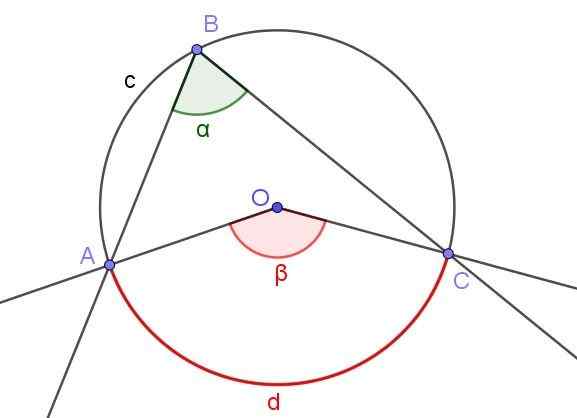Kuva 3. Rekisteröity kulma ∠ABC ja keskikulma ∠AOC, jotka alistavat saman kaaren A⌒C: n. Lähde: f. Zapata.

Kuvio 3 esittää kaksi kulmaa ∠ABC ja ∠AOC, jotka sieppaavat saman kehän kaaren A⌒C.

Jos rekisteröidyn kulman mitta on α, niin keskikulman p -mitta on kaksinkertainen rekisteröidyn kulman mittaan (β = 2 α), koska molemmat vähentävät saman mitatun kaaren D.

- Ulkokulma

Se on kulma, jonka kärki on kehän ulkopuolella ja jokainen sen sivu leikkaa kehäksi yhdessä tai useammassa pisteessä.

Omaisuus

-Sen mitta on yhtä suuri kuin kaarit katkaisevien keskikulmien puoliksi ekspressi (tai ero jaettuna 2).

Varmistaakseen, että mitta on positiivinen, puoli -ekspressin tulisi aina olla suurimman mittauksen keskikulma vähemmän alemman keskikulman mitta, kuten seuraavassa kuvassa on esitetty.

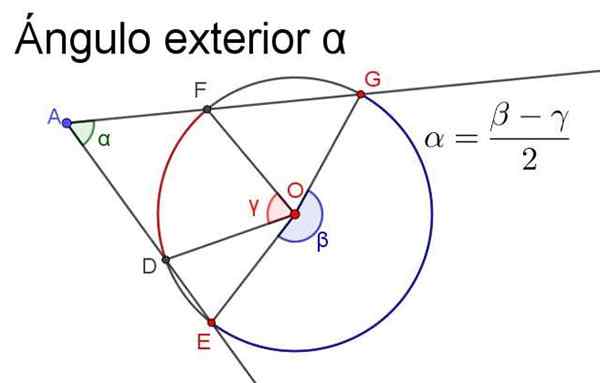Kuva 4. Ulkokulma α on yhtä suuri kuin samat kaaret subtsenin keskuksen puolivälissä. Lähde: f. Zapata.

- Sisäkulma

Sisäkulma on se, jonka kärki on kehän sisällä ja sen sivut leikataan kehään.

Voi palvella sinua: Määrityskerroin: kaavat, laskenta, tulkinta, esimerkkejä

Omaisuus 

Sen mitta on yhtä suuri kuin keskuskulman puolivälit, jotka submentoivat samaa kaaria, plus keskikulma, joka alistaa saman kaaren kuin sen pidennyskulma (tämä on sisäkulma. Sisäkulma).

Seuraava kuva kuvaa ja selventää sisäkulman ominaisuutta.

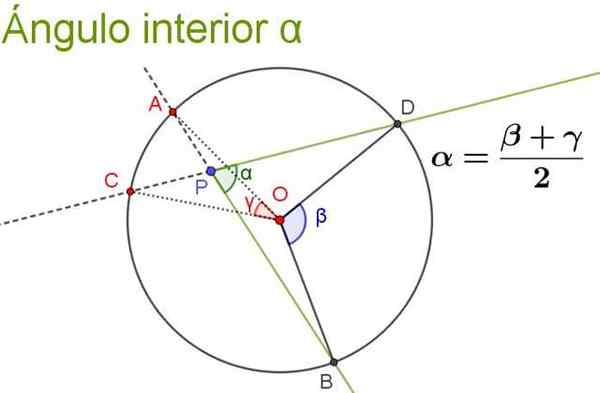Kuva 5. Sisäkulma on yhtä suuri kuin keskialueiden puolivälissä, jotka subtsen samat kaarit kuin hän itse. Lähde: f. Zapata.

Ratkaisut

- Harjoitus 1

Oletetaan. Ympyrän säde on OA = 3 cm ja kaaren D pituus π/2 cm. Määritä α- ja β -kulmien arvo.

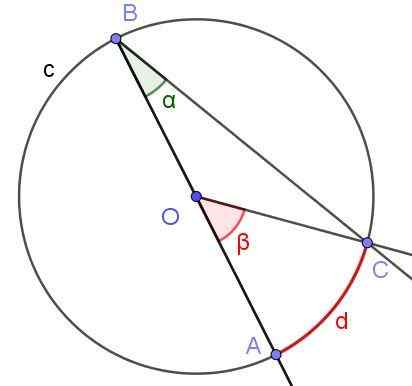Kuva 6. Rekisteröity kulma ∠ABC sivulla [BA) O: n ja keskikulman kautta ∠AOC.Lähde: f. Zapata.

Ratkaisu

Tässä tapauksessa muodostuu COB -šosceles Triange, koska [OC] = [OB]. ISCELES -kolmiossa pohjan vieressä olevat kulmat ovat samat, siksi niiden on ∠BCO = ∠ABC = α. Toisaalta ∠COB = 180º - β. Ottaen huomioon COB -kolmion sisäkulmien summa:

α + α + (180º - β) = 180º

Mistä seuraa, että 2 α = β tai mikä on ekvivalentti α = β/2, joka vahvistaa edellisen osan ominaisuuden (3), että rekisteröidyn kulman mitta on puolet keskikulmasta, kun molemmat kulmat vähentävät sama köysi [AC].

Nyt jatkamme numeeristen arvojen määrittämistä: β -kulma on keskeinen ja sen mitta radianeissa on kaaren D ja säteen r = OA: n välinen suhde, joten sen mitta on:

β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.

Voi palvella sinua: nelikulmainen: elementit, ominaisuudet, luokittelu, esimerkit

Toisaalta oli jo vahvistettu, että α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º. 

- Harjoitus 2

Kuviossa 7 kulmat α₁ ja β₂ olla sama mitta. Lisäksi kulma β₁ Sen mitat ovat 60º. Määritä kulmat β ja α.

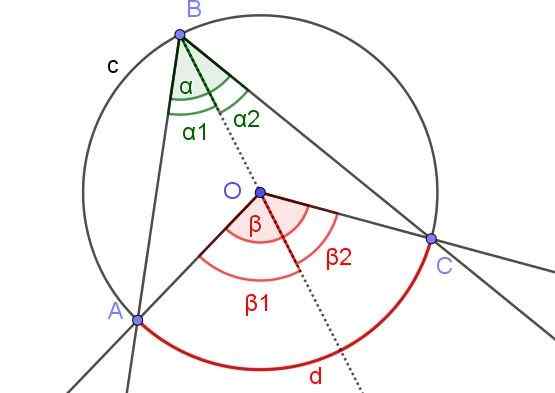Kuva 7. Kuvassa α₁ = β₂ ja β₁ = 60º. Määritä β: n ja α: n arvot. Lähde: f. Zapata.

Ratkaisu

Tässä tapauksessa on kirjoitettu kulma ∠ABC, jossa keskusta tai kehä on kulman sisällä.

Omaisuuden vuoksi (3) sinulla on α₂ = β₂ /2 ja α₁ = β₁ /2. Kuten:

α = α₁ + α₂ ja β = β₁ + β₂

Sinulla on siis:

α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Eli ominaisuuksien mukaan:

α = β / 2

Kuten meille kerrotaan, β₁ = 60º sitten:

α₁ = β₁ / 2 = 60º / 2 = 30º.

He myös kertovat meille, että α₁ = β₂ Joten tästä seuraa:

β₂ = 30º.

Kulma β on:

β₁ + β₂ = 60º + 30º = 90º.

Ja kuten α = β / 2, sitten:

α = 90º / 2 = 45º. 

Tiivistettynä:

β = 90º ja α = 45º.

Viitteet

1. Baldor, a. 1973. Geometria ja trigonometria. Keski -Amerikan kulttuuritoimitus.
2. JA. -Lla. 2003. Geometriaelementit: harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
3. Geometria 1. Kulmat kehässä. Palautettu: Edu.Xunta.On.
4. Kaikki tieteet. Ratkaistuja kulmaharjoituksia kehässä. Toipunut: Francesphysics.Blogin.com
5. Wikipedia. Rekisteröity kulma. Palautettu: on.Wikipedia.com