Toisen tasapainon ehto Selitys, esimerkit, harjoitukset

Se Toinen tasapainotila Se toteaa, että kaikkien ruumiissa toimivien voimien tuottamien vääntömomenttien tai hetkien summa on kumottava siten, että mainittu elin on staattisessa tai dynaamisessa tasapainossa.

Kreikan kirjeen kautta vääntömomentin tai voiman hetken merkitseminen τ, Matemaattisesti se ilmaistaan ​​seuraavasti:

∑ τ = 0 -

Kuvio 1. Rokkarin tasapainottamiseksi on tarpeen soveltaa toista tasapainoa. Lähde: Pxhere.

Lihavoitu kirje osoittaa tämän hetken vektorisen luonteen, joka on kumottava suhteessa kaikkiin spin -keskukseksi valituihin kohtaan. Tällä tavoin nettomomentin peruuttaminen on taataan, että esine ei alkaa kääntyä tai kääntyä.

Kuitenkin, jos objekti kiertää jo aiemmin, ja nettomomentti katoaa yhtäkkiä, kierto jatkuu, mutta jatkuvalla kulma -nopeudella.

Toista tasapainotilaa käytetään yhdessä ensimmäisen ehdon kanssa, jonka mukaan kehon voimien summan on oltava tyhjyyttä, niin että se ei liiku tai että jos se tapahtuu, se on tasaisella suorakulmiolla:

∑ F = 0 -

Molemmat olosuhteet koskevat pidennettyjä kappaleita, joiden mitat ovat mitattavissa. Kun esineen oletetaan olevan hiukkanen, ei ole mitään järkeä puhua kierroksista, ja ensimmäinen tasapainon takaaminen on riittävä.

Esimerkit

Toinen tasapainotila paljastetaan lukemattomissa tilanteissa:

Kun kiipeilee portaita

Kun tuet portaikkoa lattialla ja seinällä, tarvitsemme tarpeeksi hieroa, etenkin lattialla, varmistaaksemme, että portaikko ei liuku. Jos yritämme kiivetä tikkaat, joita tuetaan öljyisellä, märällä tai liukaslla lattialla, ei ole vaikea ennakoida, että putoamme.

Portaikon käyttämiseksi luottavaisesti on välttämätöntä, että se on staattisessa tasapainossa kiipeilyn aikana ja kun se on tarvittavassa vaiheessa.

Se voi palvella sinua: Pluto (Dwarf Planet)

Kaapin siirtäminen

Kun haluat siirtää korkeat huonekalut kaapiksi tai mihin tahansa kappaleeseen, jonka korkea on suurempi kuin sen leveä, on kätevää työntää matala piste, välttääksesi kaatumisen, tällä tavalla on todennäköisempää, että huonekalut liukuvat sen sijaan kääntyä ja makaa.

Tällaisissa olosuhteissa huonekalut eivät välttämättä ole tasapainossa, koska sitä voidaan siirtää nopeasti, mutta ainakaan se ei käänny.

Parvekkeet

Parvekkeet, jotka erinomaiset rakennukset on rakennettava.

Dielektrisyys ulkoisilla sähkökentillä

Kun sijoitat dielektrisen materiaalin ulkoiseen sähkökentälle, molekyylit liikkuvat ja pyörivät omaksumaan tasapainoasento, luomalla sähkökenttä materiaalin sisälle.

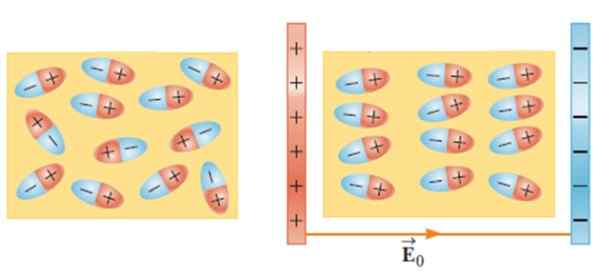Kuva 2.- Ilman ulkoista sähkökenttää dipolit satunnaistetaan (vasen). Ulkoinen kenttä soveltaa vääntömomenttia dielektrisissä molekyyleissä ja nämä järjestetään uudelleen. Lähde: Serway, R. Fysiikka tieteen ja tekniikan fysiikka.

Tämä vaikutus saa lauhduttimen kapasiteetin lisääntymään, kun sen panssarin väliin otetaan materiaali, kuten lasi, kumi, paperi tai öljy.

Merkkejä ja lamput

On yleistä, että monet tilat ripustaavat ilmoitukset rakennuksen seinälle, niin että ne ovat näkyvissä ohikulkijoille.

Juliste kiinnitetään palkki ja kaapeli, jotka molemmat kiinnitetään seinälle tukien avulla. Erilaisten voimien, jotka toimivat.

Puiston heijastin voidaan myös sijoittaa tällä tavalla, kuten seuraavassa kuvassa:

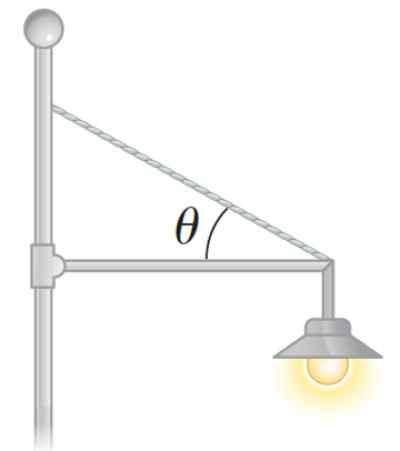Kuva 3. Staattinen saldovalaisin. Lähde: Serway. Fysiikka tieteen ja tekniikan fysiikka.

Kuinka laskea voiman nettomomentti tai nettomomentti?

Vääntömomentti tai voimamomentti, merkitty τ jompikumpi M Joissakin teksteissä se lasketaan aina suhteessa johonkin pisteeseen, jossa kierto -akseli kulkee.

Se määritellään vektorituotteeksi sijaintivektorin välillä r -, Se on suunnattu mainitulta akselilta voiman ja lujuuden levittämispisteeseen F-

Voi palvella sinua: Termodynaaminen tasapaino: Luokat ja sovellukset

τ = r - × F

Vektorina on välttämätöntä ilmaista vääntömomentti, joka antaa sen suuruuden, suunnan ja merkityksen. Suuruus on annettu:

τ = RF.synti θ

Oikea sääntö vektorituotteelle

Kun ongelma on tasossa, vääntömomentin osoite on kohtisuorassa paperille tai näytölle ja suunta määritetään oikeanpuoleisen säännön perusteella, johon indeksi osoittaa kohti r -, Keskisormi F ja peukalo signaalit.

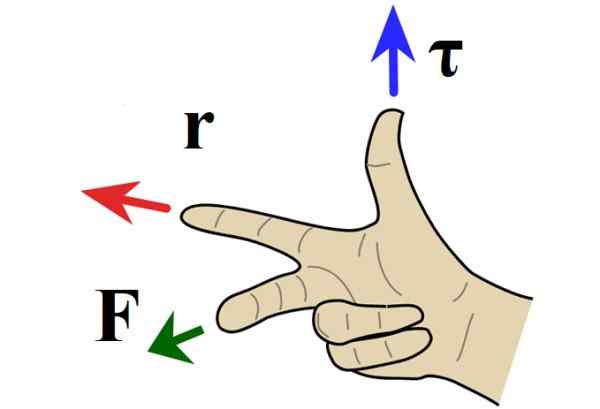Kuva 4. Oikeanpuoleinen sääntö vektorituotteelle. Lähde: Wikimedia Commons.

Kun vääntömomentti osoittaa paperista, kierto on vastakkaiseen suuntaan kuin kelloleulat ja sille on annettu positiivinen merkki yleissopimuksella. Jos sen sijaan vääntömomentti on suunnattu arkkiin, kierto on käsien suuntaan ja negatiivinen merkki.

Verkkomomentin löytämiseksi valitaan kätevä piste laskelmalle, joka voi olla se, jossa suurin määrä voimia. Tässä tapauksessa näiden voimien hetki on tyhjä, sillä sillä on sijaintivektori r - suuruusluokka 0.

Voit valita minkä tahansa pisteen, joka tarjoaa tarpeeksi tietoa tuntemattoman puhdistamiseksi, joka vaatii ratkaisemisen ongelmaa. Katsotaanpa se yksityiskohtaisemmin.

Liikuntaa

Seuraavan kuvan heijastimessa on 20 kg massaa, ja sitä tukee vaakasuora ohut palkki, halveksittava massa ja pituus L, joka on nivelletty pylvääseen. Kaapeli, myös valo, joka auttaa ylläpitämään heijastinta, muodostaa kulman θ = 30 º palkin kanssa. Laskea:

a) kaapelin jännitys

b) voiman F suuruus, jonka pylväs käyttää tangossa saranan läpi.

Ratkaisu

Käytämme ensimmäistä tasapainoolosuhteita ∑ F = 0 - kaaviossa esitetyille voimille:

Voi palvella sinua: absorboitunut lämpö: Kaavat, kuinka se lasketaan ja ratkaistaan ​​harjoituksia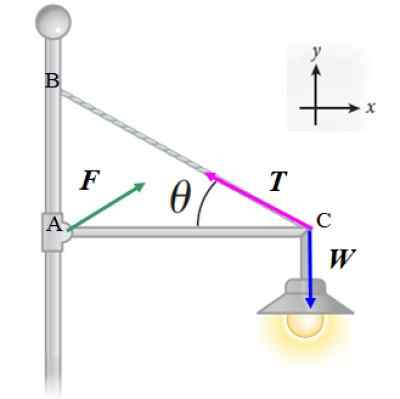

F + T + W = 0

Huomaa, että suuruus ja suunta F Niitä ei ole vielä määritetty, mutta oletamme, että sillä on kaksi komponenttia: f_x ja f_ja. Tällä tavalla saamme kaksi yhtälöä:

F_x -T. cos θ = 0

F_ja - W + t⋅ sin θ = 0

Nyt sovelletaan toinen tasapainotila, valitsemalla kohta A, koska emme tiedä F eikä T. Kun valitaan tätä pistettä, vektori r -_-Lla on tyhjä, siis hetki F on tyhjä ja F Se ei näy yhtälössä:

-W⋅l + t⋅sen θ⋅l = 0

Siksi:

T.synti θ.L = w.Lens

T = w/sen θ = (20 kg x 9.8 m/s²) / Sin 30 º = 392 n

T: n suuruuden tietäminen voimme puhdistaa komponentin f_x-

F_x = T⋅ cos θ = 392 cos 30º n = 339. 5 n

Ja sitten komponentti f_ja-

F_ja = W - T⋅ sin θ = (20 kg x 9.8 m/s²) - 392⋅sen 30 º = 0

Sitten voimme ilmaista F Niin:

F = 339.5 n x

Siksi se on vaakasuora voima. Tämä johtuu siitä, että katsomme, että baarilla oli halveksittava paino.

Jos piste C olisi valittu laskemaan tuloksena oleva hetki, vektorit r -_T ja r -_{W -} Siksi ne ovat tyhjiä:

M = f_{Y raja}L = 0

On päätelty, että f_ja = 0. Täten:

- W + t⋅ sin θ = 0

T = w/ sin θ

Joka on sama tulos, joka alun perin saadaan valitsemalla piste A kuin paikka, jossa kierto -akseli kulkee.

Kiinnostavia teemoja

Tasapainoolosuhteet.

Ensimmäinen tasapainon kunto.

Viitteet

1. Bedford, 2000. -Lla. Tekniikan mekaniikka: staattinen. Addison Wesley.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 4. Hiukkasjärjestelmät. Toimittanut Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
5. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.