Reynolds -numero mitä se on, miten se lasketaan, harjoitukset

Hän Reynolds -numero (R -_ja) Se on mittasuhteen ja liikkeenesteen viskoosien voimien välinen suhde. Inertiaaliset voimat määräävät Newtonin toinen laki ja ne ovat vastuussa nestekiihdyn maksimaalisesta. Viskoosit voimat ovat voimia, jotka vastustavat nesteen liikkumista.

Reynolds -lukua käytetään minkä tahansa tyyppiseen nestevirtaukseen, kuten virtaus ympyrä- tai ei -ympyräkanavissa, avoimissa kanavissa ja virtaus upotettujen kappaleiden ympärillä.

Reynolds -luvun arvo riippuu tiheydestä, viskositeetista, nesteen nopeudesta ja nykyisen reitin mitoista. Nesteen käyttäytyminen kitkasta johtuvan energian määrästä riippuen se riippuu siitä, onko virtaus laminaarinen, turbulentti vai välituote. Tästä syystä on tarpeen löytää tapa määrittää virtaustyyppi.

Yksi tapa määrittää se on kokeellisten menetelmien avulla, mutta vaatii paljon tarkkuutta mittauksissa. Toinen tapa määrittää virtaustyyppi on saada Reynolds -luku.

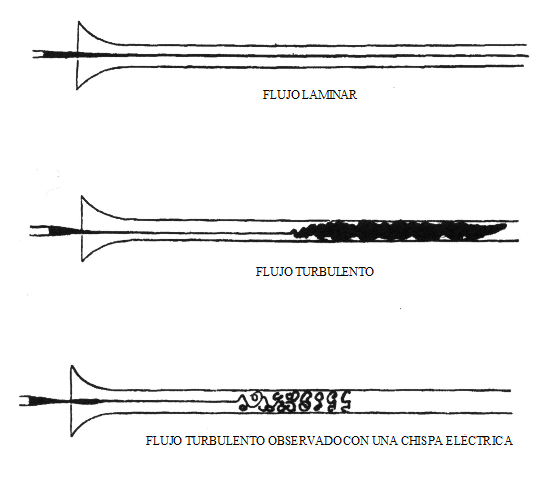
Osborne Reynoldsin havaitsema vesivirta [Osborne Reynolds (https: // commons.Wikimedia.org/wiki/tiedosto: reynolds_observitions_urbulence_1883.Svg)]

Vuonna 1883 Osborne Reynolds havaitsi, että jos tämän ulottumattoman numeron arvo tunnetaan, virtauksen tyyppi, joka kuvaa mitä tahansa nesteen johtamistilannetta, voidaan ennustaa.

[TOC]

Mikä on Reynoldsin numero?

Reynoldsin lukumäärä määrittää nesteen käyttäytymisen, toisin sanoen, onko nesteen virtaus laminaarinen vai turbulentti. Virtaus on laminaarinen, kun viskoosit voimat, jotka vastustavat nesteen liikkumista, ovat niitä, jotka hallitsevat ja nestettä liikkuvat riittävän pienellä nopeudella ja läpikäymisellä.

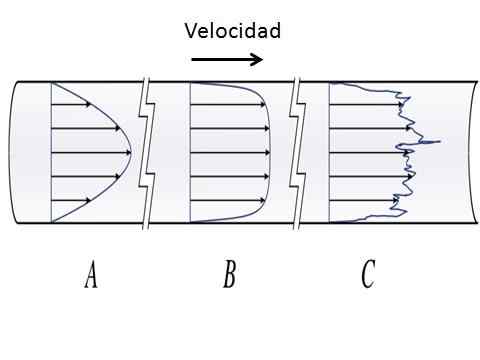Nesteen nopeus, joka liikkuu pyöreän kanavan läpi, laminaarivirtaukselle (A) ja turbulenttivirtaukselle (B ja C). [Kirjoittanut Olivier Cleynen (https: // commons.Wikimedia.org/wiki/tiedosto: putki_flow_velocity_distribusion_laminar_turbulent.Svg)]

Laminaarivirtauksella varustettu neste käyttäytyy ikään kuin ne olisivat äärettömiä kerroksia, jotka liukuvat muiden yli, järjestyksessä, sekoittamatta. Pyöreissä kanavissa laminaarivirtaus on parabolinen nopeusprofiili, ja maksimiarvot kanavan keskellä ja minimiarvot kanavan pinnan lähellä olevissa kerroksissa. Reynolds -numeron arvo laminaarivirtauksessa on R -_ja<2000.

Virtaus on turbulenssia, kun inertiaaliset voimat ovat hallitsevia ja neste liikkuu epäsäännöllisen nopeuden ja suuntaviivojen vaihtelevilla muutoksilla. Turbulentti virtaus on erittäin epävakaa ja liikuntasiirrot nestepartikkelien välillä.

Voi palvella sinua: kalsiumfluori (CAF2): rakenne, ominaisuudet, käyttötarkoitukset

Kun neste kiertää pyöreässä kanavassa, turbulenttisella virtauksella, nestekerrokset leikkaavat toistensa kanssa muodostuvien pyörteiden kanssa ja niiden liike on yleensä kaoottinen. Reynolds -luvun arvo turbulenssista virtauksesta pyöreässä kanavassa on R -_ja > 4000.

Siirtyminen laminaarivirtauksen ja turbulenttisen virtauksen välillä tapahtuu Reynolds -luvun arvoille 2000 ja 4000.

Kuinka se lasketaan?

Reynolds -luvun laskemiseen pyöreässä poikkileikkauskanavassa käytetty yhtälö on:

R -_ja = ρvd/η

ρ = Nesteen tiheys (kg/m³-A

V = Virtausnopeus (m³/s-A

D -d = Lineaarinen ulottuvuus ominainen nestematka, joka pyöreän kanavan tapauksessa edustaa halkaisijaa.

η = nesteen dynaaminen viskositeetti (Paa.s-A

Viskositeetin ja tiheyden välinen suhde määritellään kinemaattiseksi viskositeetiksi v = η/ρ, Ja yksikkösi on m²/s.

Reynolds -luvun yhtälö kinemaattisesta viskositeetista riippuen on:

R -_ja = Vd/v

Kanavissa ja kanavissa, joissa ei ole ympyräpoikkileikkauksia, ominainen ulottuvuus tunnetaan hydraulisena halkaisijana D -d_H ja edustaa nestepolun yleistä ulottuvuutta.

Yleinen yhtälö Reynolds -luvun laskemiseen kanavien kanssa ei -ympyräkäyttöisissä poikkileikkauksissa on:

R -_ja = ρv 'd_H /η

V '= Keskimääräinen virtausnopeus =Mennä

Hydraulinen halkaisija D -d_H vahvistaa alueen välisen suhteen -Lla virtausvirran poikkileikkauksesta ja märästä kehästä P_M .

D -d_H = 4A/P_M

Märkä kehä P_M Kanavan seinien pituuksien summa tai kanava, joka on kosketuksessa nesteen kanssa.

Voit myös laskea esinettä ympäröivän nesteen Reynolds -määrän. Esimerkiksi nesteeseen upotettu pallo liikkumalla nopeudella V. Pallo kokee vetovoiman F_{R -} Stokes -yhtälön määrittelemä.

F_{R -} = 6πrvη

R - = Sphere Radio

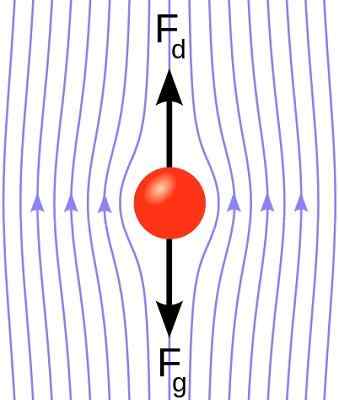Pallonopeusprofiili upotettu nesteeseen. Vetovoima vastustaa painovoimaa. [Kirjoittanut Kraaiennest (https: // commons.Wikimedia.org/wiki/tiedosto: stokes_sphere.Svg)]

Reynolds -alueen lukumäärä nopeudella V Nesteen upotettu on:

R -_ja = ρv r /η

R -_ja<1 cuando el flujo es laminar y R_ja > 1 Kun virtaus on turbulentti.

Ratkaisut

Alla on kolme Reynolds -numeron sovellusharjoitusta: Pyöreä kanava, suorakulmainen kanava ja pallo upotettu.

Se voi palvella sinua: Leikkaus: miten lasketaan ja ratkaistaan

Reynolds -numero pyöreässä kanavassa

Laske reynolds -propeeniglykolin lukumäärä 20 °C Pyöreän halkaisijan kanava 0,5 cm. Virtausnopeuden suuruus on 0,15m³/s. Mikä on virtaustyyppi?

D -d =0,5 cm = 5.10^-3m (ominainen ulottuvuus)

Nestetiheys on ρ = 1 036 g/cm³= 1036 kg/ m³

Nesteen viskositeetti on η = 0,042 pa · s = 0,042 kg/m.s

Virtausnopeus on V = 0,15m³/s

Reynolds -lukuyhtälöä käytetään pyöreässä kanavassa.

R -_ja =ρSINÄ/η

R -_ja = (1036 kg/ m³X0,15m³/s x 5.10^-3m)/(0,042 kg/m.s) = 18,5

Virtaus on laminaarinen, koska Reynolds -luvun arvo on alhainen suhteessa R -_ja<2000

Reynolds -numero suorakaiteen muotoisessa kanavassa

Määritä etanolivirtauksen tyyppi, joka virtaa 25 ml/min nopeudella suorakaiteen muotoisessa putkessa. Suorakulmaisen osan mitat ovat 0,5 cm ja 0,8 cm.

Tiheys ρ = 789 kg/m³

Dynaaminen viskositeetti η = 1 074 MPa · S = 1 074.10^-3 kg/m.s

Ensinnäkin keskimääräinen virtausnopeus määritetään.

V ' =Mennä

V = 25 ml/min = 4,16.10^-7m³/s

Poikkileikkaus on suorakaiteen muotoinen, joiden sivut ovat 0,005 m ja 0,008 metriä. Ristien alue on A = 0,005m x0,008m = 4.10^-5m²

V ' = (4.16.10^-7m³/s) /(4.10^-5m²) = 1,04 × 10^-2neiti

Märkä kehä on suorakulmion sivujen summa.

P_M=0,013m

Hydraulinen halkaisija on D -d_H = 4A/P_M

D -d_H = 4 × 4.10^-5m²/0.013m

D -d_H= 1,23.10^-2m

Reynoldsin numero saadaan yhtälöstä R -_ja = ρv 'd_H /η

R -_ja = (789 kg/m³X1.04 × 10^-2m/s x1.23.10^-2m)/ 1 074.10^-3 kg/m.s

R -_ja = 93974

Virtaus on turbulentti, koska Reynoldsin luku on erittäin suuri (R -_ja> 2000)

Reynoldsin määrä pallo on upotettu nesteeseen

Pallomainen hiukkas, polysireenilateksista, jonka säde on R -= 2000 nm Se heitetään pystysuoraan veteen alkuperäisen suuruuden nopeudella V_{0 -}= 10 m/s. Määritä veteen upotetun hiukkasen reynolds -lukumäärä

Hiukkasten tiheys  ρ = 1,04 g/cm³ = 1040 kg/m³

R -= 2000Nm = 0,000002 metriä

Vesitiheys ρ_Ag= 1000 kg/m³ 

Goo η =0,001 kg/(m · s)

Reynoldsin numero saadaan yhtälöllä R -_ja = ρv r /η

R -_ja = (1000 kg/m³x10 m/s x 0,000002 m)/ 0,001 kg/(m · s)

R -_ja = 20

Reynoldsin numero on 20. Virtaus on myrskyistä.

Sovellukset

Reynoldsin lukumäärällä on tärkeä rooli nesteen mekaniikassa ja lämmönsiirrossa, koska se on yksi pääparametreista, jotka kuvaavat nestettä. Jotkut sovelluksistasi mainitaan alla.

Se voi palvella sinua: paikallaan olevat aallot: kaavat, ominaisuudet, tyypit, esimerkit

1-sitä käytetään simuloimaan nestemäisillä pinnoilla liikkuvien organismien liikettä, kuten: bakteerit, jotka on ripustettu veteen, jotka uivat nesteen läpi ja tuottavat satunnaista sekoittamista.

2-IT: llä on käytännöllisiä sovelluksia putkien virtauksessa ja nestemäisissä kiertokanavissa, suljetuissa virtauksissa, etenkin huokoisissa väliaineissa.

3-in neste- ja emulsioihin upotettujen kiinteiden hiukkasten suspensiot.

4-Reynolds-lukumäärä käytetään tuulitunnelikokeissa useiden pintojen aerodynaamisten ominaisuuksien tutkimiseksi, etenkin lentokoneiden lentojen tapauksessa.

5-sitä käytetään hyönteisten liikkumisen mallintamiseen ilmassa.

6-Kemiallinen reaktorisuunnittelu vaatii Reynolds-numeron käyttöä virtausmallin valitsemiseksi kuormitushäviöiden, energiankulutuksen ja lämmönsiirto-alueen mukaan.

7-in Elektronisten komponenttien lämmönsiirto (1).

8-tutustunut puutarhojen ja hedelmätarhojen kasteluprosessi, jossa tarvitaan putkista tulevaa vesivirtausta. Näiden tietojen saamiseksi määritetään hydraulisen kuorman menetys, joka liittyy veden ja putkien seinien väliseen kitkalle. Kuorman menetys lasketaan, kun Reynolds -luku saadaan.

Tuulitunneli [kirjoittanut Juan Kulichevsky (https: // commons.Wikimedia.org/wiki/tiedosto: t%c3%banel_de_vento_ (35351654140).Jpg)]

Biologiset sovellukset 

Biologiassa elävien organismien liikkumisen tutkiminen veden kautta tai nesteissä, joilla on veden kaltaisia ​​ominaisuuksia, vaatii Reynolds -numeron saamisen, mikä riippuu organismien koosta ja niiden liikkuvan nopeuden koosta ja nopeudesta, jolla ne liikkuvat.

Yksisoluisilla bakteereilla ja organismeilla on erittäin matala Reynolds -luku (R -_ja<<1) Tämän seurauksena virtauksella on laminaarinen nopeusprofiili, jossa on viskoosien voimien hallussapito.

Muurahaisten lähellä olevilla organismeilla (enintään 1 cm) on Reynolds -lukumäärä luokkaa 1, mikä vastaa siirtymäjärjestelmää, jossa kehoon vaikuttavat inertiaalit ovat yhtä tärkeitä kuin nesteen viskoosit voimat.

Suuremmissa organismeissa, kuten People Reynoldsin lukumäärä, on erittäin suuri (R -_ja>> 1-A.

Viitteet

1. Matala-Reynolds -lukujen levitys Turbulenttivirtausmallit elektronisen komponentin lämmönsiirron ennustamiseen. Rodgers, P ja Eveloy, V. NV: S.n., 2004, IEEE, Vol. 1, p. 495-503.
2. Mott, r l. Käytetty nestemekaniikka. Berkeley, Kalifornia: Pearson Prentice Hall, 2006, Vol. Yllyttää.
3. Collieu, M ja Powney, D J. Materiaalien mekaaniset ja epätavalliset ominaisuudet. New York: Crane Russak, 1973.
4. Kay, J M ja Nedderman, R M. Johdatus neste mekaniikkaan ja lämmönsiirtoon. New York: Cambridge University Press, 1974.
5. Happel, J ja Brenner, H. Nesteiden ja kuljetusprosessin mekaniikka. Hingham, MA: Martinuss Nijhoff Publishers, 1983.