Kvantinumerot mitä käyttö on ja mitkä ovat

Se nKvantti Niitä käytetään kuvaamaan atomin elektronien kvanttitilaa, ja ne ovat peräisin Schrödinger -yhtälön liuoksesta yksinkertaisimmille: vety.

Schrödingerin yhtälö on differentiaaliyhtälö, jonka ratkaisut ovat Aaltofunktiot ja ne merkitään kreikkalaisella kirjaimella ψ. Äärettömiä ratkaisuja voidaan nostaa, ja sen neliö vastaa todennäköisyyttä löytää elektroni pienellä avaruusalueella, nimeltään orbitaali-.

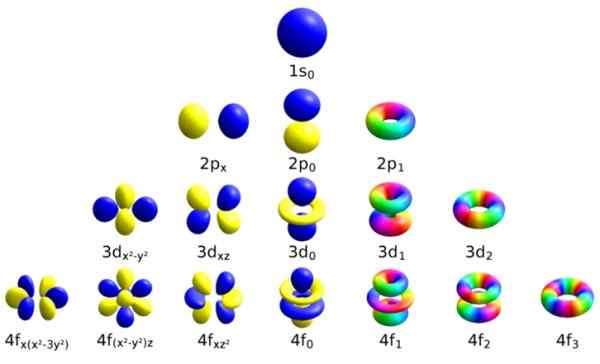
Jokainen näistä atomiorbitaalista erotetaan tietyllä kvanttilukujoukolla. Lähde: Wikimedia Commons.

Jokaisella kiertoradalla on määritellyt ominaisuudet, jotka erottavat sen muista, kuten energia, kulmavirta ja spin, elektronin täysin kvanttiominaisuus ja joka on muun muassa magneettisten vaikutusten suhteen.

Tapa tunnistaa jokainen kiertorata on erottaa se sitä kuvaavien numeroiden avulla, ja nämä ovat juuri kvantinumerot:

-N: on tärkein kvanttiluku.

-ℓ: Azimutaalinen kvanttiluku.

-m_ℓ, Se on magneettinen luku.

-m_s, Spin -numero.

[TOC]

Mitä ovat kvanttinumerot?

Kvanttinumerot kuvaavat atomin sisällä olevien elektronien tilaa. Että atomimalli, jossa elektroni kääntyy ytimen ympäri.

Siksi Tanskan Niels Bohr (1885-1962) teki vuonna 1913 lihavoidun ehdotuksen: Elektroni löytyy vain tietyistä vakaista kiertoradoista, joiden koko riippuu kokonaislukuista nimeltään n.

Myöhemmin, vuonna 1925, itävaltalainen fyysinen Erwin Schrödinger (1887-1961) nosti differentiaaliyhtälön osittaisissa johdannaisissa, joiden liuokset kuvaavat vetyatomia. Ovat alussa mainitut aaltofunktiot ψ.

Tämä differentiaaliyhtälö sisältää kolme alueellista koordinaattia ja aikaa, mutta kun sitä ei sisälly, Schrödinger -yhtälön ratkaisu on analoginen kuin paikallaan olevan aallon (aalto, joka leviää tiettyjen rajojen välillä).

Aaltofunktiot

Schrödingerin riippumaton aikayhtälö ratkaistaan ​​pallomaisissa koordinaateissa ja ratkaisu on kirjoitettu kolmen toiminnon tuloksena, yksi jokaiselle alueelliselle muuttujalle. Tässä koordinaattijärjestelmässä Cartesian -akselien koordinaattien käytön sijasta x, ja ja z -z Koordinaatteja käytetään r -, θ ja φ. Tällä tavalla:

Voi palvella sinua: Rinnakkaispiiri

ψ (r, θ, φ) = r (r) ⋅f (θ) ⋅g (φ)

Aaltofunktio on aineeton, kvanttimekaniikasta huolimatta se kertoo meille, että neliön amplitudi:

| ψ (r, θ, φ) |²

Toisin sanoen, että aaltofunktion moduuli tai absoluuttinen arvo, neliö, on todellinen luku, joka edustaa elektronin löytämisen todennäköisyyttä tietyllä alueella sen ympärillä, jonka koordinaatit ovat r -, θ ja φ.

Ja tämä tosiasia on jotain konkreettisempaa ja konkreettisempaa.

Aaltofunktion löytämiseksi sinun on ratkaistava kolme tavallista differentiaaliyhtälöä, yksi jokaiselle muuttujalle r -, θ ja φ.

Kunkin yhtälön liuokset, jotka ovat funktioita r (r), f (θ) ja g (φ), sisältävät kolme ensimmäistä mainittua kvantinumeroa.

Mitkä ovat kvantinumerot?

Seuraavassa kuvaamme lyhyesti kunkin kvantinumeron luonnetta. Kolme ensimmäistä, kuten edellä todettiin, syntyvät Schrödinger -yhtälön ratkaisuista.

Paul Dirac (1902 - 1984) lisäsi neljännen määrän vuonna 1928.

Pääkvantinumero

Se on merkitty n ja osoittaa sallitun kiertoradan koon sekä elektronin energian. Mitä korkeampi sen arvo, sitä enemmän ytimen elektroni on ja sen energia on, mutta vastineeksi se vähentää sen vakautta.

Tämä luku syntyy R (R) -toiminnosta, joka on todennäköisyys löytää elektroni tietyltä etäisyydeltä r - ytimestä, joka määritetään:

 Missä seuraavat vakiot osallistuvat:

-Planck -vakio: H = 6,626 × 10 ^{-3. 4} J -.s
-Elektronimassa m_ja = 9.1 × 10^-31 kg
-Elektronikuorma: E = 1.6 × 10^-19 C.
-Sähköstaattinen vakio: k = 9 × 10 ⁹ N.m²/C²

Kun n = 1 vastaa Bohr -sädettä, jonka arvo on noin 5.3 × 10⁻¹¹ m.

Ensimmäistä kerrosta lukuun ottamatta muut jaetaan alakannaksi tai ala -tasoiksi. Jokaisella kerroksella on energiaa volttielektronina: Annetaan:

Voi palvella sinua: mekaaniset aallot: ominaisuudet, ominaisuudet, kaavat, tyypit

Termi EV "Elektronivoltti" tarkoittaa, että energiayksikkö käytetään usein kvanttifysiikan alueella. Missä n = 1, 2, 3, 4 .. . ja jokainen n -arvo vastaa a kerros, Se on merkitty isoilla kirjaimilla:

• K (n = 1)
• L (n = 2)
• M (n = 3)
• N (n = 4)
• Tai (n = 5)
• P (n = 6)
• Q (n = 7).

Teoriassa N: lle ei ole ylärajaa, mutta käytännössä havaitaan, että se saavuttaa vain n = 8. Mastin mahdollinen energia vastaa n = 1 ja on Peruste.

Atsimutaalinen kvantti- tai kulmavirta

Kursivoisella kirjaimella merkitty tämä luku määrittää kiertoradan muodon, kun se kvantifioi elektronin kiertoradan kulmanmomentin suuruuden.

Voit ottaa esimerkiksi kokonaiset ja positiiviset arvot välillä 0 ja N-1:

-Kun n = 1, sitten ℓ = 0 ja on yksi ala -taso.

-Jos n = 2, niin ℓ voi olla arvon arvoinen 0 tai 1, joten sinulla on kaksi ala -tasoa.

-Ja jos n = 3, niin ℓ olettaa arvot 0, 1 ja 2 ja on 3 alatasoista.

Sitä voidaan seurata määräämättömäksi ajaksi, vaikka kuten aiemmin todettiin, käytännössä N saavuttaa jopa 8. Sub -tasot merkitään kirjaimilla: s, p, d -d, F ja g Ja ne kasvavat energiassa.

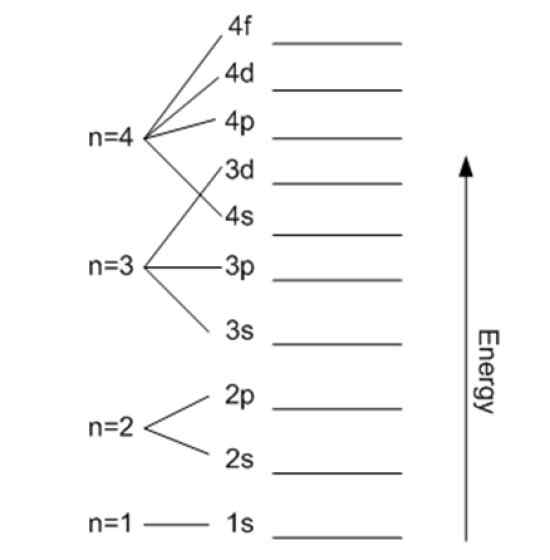Energia liittyy päämäärän lukumäärään. Lähde: Wikimedia Commons.

Magneettinen kvanttiluku m_ℓ

Tämä luku päättää kiertoradan suuntauksen avaruudessa ja sen arvo riippuu ℓ.

Tietylle ℓ: lle on (2ℓ+1) kokonaisia ​​arvoja m _ℓ, vastaavat kiertoradat. Nämä ovat:

-ℓ, ( - ℓ+1),… 0,… (+ℓ -1),+ℓ.

Esimerkki

Jos n = 2, tiedämme, että ℓ = 0 ja ℓ = 1, niin m _ℓ Ota seuraavat arvot:

-ℓ = 0: m _ℓ = 0.
-ℓ = 1: m _ℓ = -1, m _ℓ = 0, m _ℓ = +1

Orbitaalilla n = 2 on kaksi alatasoa, ensimmäinen n = 2, ℓ = 0 ja m _ℓ = 0. Sitten meillä on toinen alataso: n = 2, ℓ = 1, 3 kiertoradalla:

• N = 2, ℓ = 1, m _ℓ = -1
• N = 2, ℓ = 1, m _ℓ = 0
• N = 2, ℓ = 1, m _ℓ = +1

Kolmella kiertoradalla on sama energia, mutta erilainen spatiaalinen suuntaus.

Kvantti lukumäärä spin m_s

Kun ratkaiset Schrödinger -yhtälön kolmessa ulottuvuudessa, jo kuvattu lukumäärä syntyy. Vedyssä havaitaan kuitenkin vielä enemmän rakennetta kuin nämä luvut eivät riitä selittämään.

Se voi palvella sinua: Gase Constant: Mikä on, laskenta ja esimerkit

Siksi vuonna 1921 toinen fysiikka, Wolfgang Pauli, ehdotti neljännen numeron olemassaoloa: spin -numero m_s, Se vie arvot +½ tai -½.

Tällä numerolla kuvataan erittäin tärkeä elektronin ominaisuus, mikä on pyöriä, Sana, joka tulee englannista pyöriä (Käännä itsesi). Ja spin puolestaan ​​liittyy atomin magneettisiin ominaisuuksiin.

Yksi tapa ymmärtää spin on kuvitella, että elektroni käyttäytyy kuin pieni magneettinen dipoli (magneetti, jossa on pohjoinen ja eteläinen pylväät) oman akselinsa ympärillä olevan kierroksen ansiosta. Käännös voi olla samaan suuntaan kuin kelloneulat tai vastakkaiseen suuntaan.

Vaikka Pauli ehdotti tämän määrän olemassaoloa, Otto Sternin ja Walter Gerlachin vuonna 1922 suorittaman kokeen tulokset olivat jo ennakoineet sitä.

Nämä tutkijat onnistuivat jakamaan hopea -atomien säteen käyttämällä ei -yhtenäistä magneettikenttää.

M: n arvo_s Se ei riipu n, ℓ ja M _ℓ. Graafisesti sitä edustaa nuoli: ylöspäin suuntautuva nuoli osoittaa aikataulun ja yhden antihoranin alas.

Paulin syrjäytymisperiaate

Atomin elektronien käyttäytyminen on yhteenveto Paulin sulkemisen periaatteessa, jossa todetaan, että kaksi atomin elektronia ei voi olla samassa kvanttitilassa.

Siksi jokaisella elektronilla on oltava erilainen kvanttilukujen n, ℓ, m _ℓ ja m_s.

Kvanttimäärien merkitys ja tämä periaate on jaksollisen taulukon elementtien ominaisuuksien ymmärtämisessä: Elektronit on järjestetty kerroksiin N: n mukaan ja sitten alaryhmissä ℓ: n ja muun numeron mukaan.

Viitteet

1. Alonso, m. 1971. Kvantti- ja tilastolliset perusteet. Inter -American Educational Fund.
2. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
3. Chang, R. 2013. Kemia. 11Va. Painos. MC Graw Hill Education.
4. Eisberg-Resnick. 1989. Kvanttifysiikka. Limusa - Wiley.
5. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
6. Rex, a. 2011. Fysiikan perusteet. Pearson.
7. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.