Järkevä lukumäärä Ominaisuudet, esimerkit ja toiminnot

Se rationaaliset numerot Ne ovat kaikki numerot, jotka voidaan saada kahden kokonaisluvun jakautumisena. Esimerkkejä rationaalisista numeroista ovat: 3/4, 8/5, -16/3 ja seuraavat kuvassa esiintyvät. Järkevällä numerolla osoitetaan jakaminen, jos se on mahdollista tehdä myöhemmin tarvittaessa.

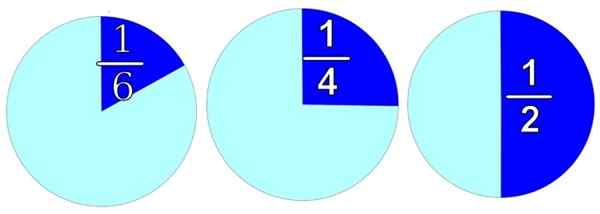
Kuvassa kaikki esineet on edustettu, pyöreä mukavuus. Jos haluamme jakaa sen kahteen yhtä suureen osaan, kuten oikealla, meillä on kaksi puolikkaata ja jokainen on 1/2.

Kuvio 1. Järkevä lukumäärä käytetään jakamaan kokonainen eri osiin. Lähde: FreesVG.

Jakamalla se 4 yhtä suureen osaan, saamme 4 kappaletta ja jokainen on arvoinen 1/4, kuten keskustassa. Ja jos joudut jakamiseen 6 yhtä suureen osaan, niin jokainen osa olisi arvoinen 1/6, jonka näemme vasemmalla olevassa kuvassa.

Tietysti voimme jakaa sen myös kahteen ei -tasa -arvoiseen osaan, esimerkiksi voimme pitää 3/4 osaa ja tallentaa 1/4 osaa. Muut divisioonat ovat myös mahdollisia, kuten 4/6 osaa ja 2 osaa. Tärkeää on, että kaikkien osien summa on 1.

Tällä tavalla on selvää, että rationaalisilla numeroilla voit jakaa, laskea ja jakaa esimerkiksi ruokaa, rahaa, maata ja kaikenlaisia ​​esineitä fraktioissa. Ja niin lukumäärän määrää, joka voidaan tehdä numeroilla.

Rationaaliset numerot voidaan myös ilmaista desimaalisesti, kuten seuraavissa esimerkeissä voidaan nähdä:

1/2 = 0,5

1/3 = 0,3333…

3/4 = 0,75

1/7 = 0,142857142857142857…

Myöhemmin ilmoitamme, kuinka siirtyä yhdestä toiseen esimerkeillä.

[TOC]

Järkevälukuominaisuudet

Rationaalisilla numeroilla, joiden sarjalla merkitsemme kirjaimella Q, on seuraavat ominaisuudet:

-Q sisältää luonnolliset numerot n ja kokonaiset N -numerot.

Kun otetaan huomioon mikä tahansa numero -lla Se voidaan ilmaista toistensa ja 1: n osamääräksi, on helppo nähdä, että on myös luonnollisia lukuja ja kokonaislukuja.

Siten luonnollinen numero 3 voidaan kirjoittaa murto -osana ja myös -5:

3 = 3/1

-5 = -5/1 = 5/-1 = -(5/1)

Tällä tavalla se on numeerinen joukko, joka kattaa suuremman määrän numeroita, jotain erittäin välttämätöntä, aseta "pyöreät" numerot eivät riitä kuvaamaan kaikkia mahdollisia operaatioita.

Voi palvella sinua: 90 jakajaa: Mitkä ovat ja selitys

-Rationaalilukuja voidaan lisätä, vähentää, kertoa ja jakaa, operaation tulos on rationaalinen luku: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Jokaisen parin rationaalisen numeron välillä voidaan aina löytää toinen rationaalinen luku. Itse asiassa kahden rationaalisen luvun välillä on rationaalinen ääretön. 

Esimerkiksi rationaalisten 1/4 - 1/2 välillä ovat rationaalisia 3/10, 7/20, 2/5 (ja paljon muuta), jotka voidaan varmistaa ilmaisemaan ne desimaaleina.

-Mikä tahansa järkevä luku voidaan ilmaista seuraavasti: i) kokonaisluku tai ii) rajoitettu desimaali (tiukka) tai sanomalehti: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,1666666…

-Samaa lukua voidaan edustaa äärettömillä vastaavilla fraktioilla ja ne kaikki kuuluvat Q: hen. Katsotaanpa tätä ryhmää:

Kaikki edustavat desimaalia 0.428571 ..

-Kaikista vastaavista fraktioista, jotka edustavat samaa määrää, peruuttamaton fraktio, yksinkertaisin kaikista, on Kanoninen edustaja tuo lukumäärä. Edellisen esimerkin kanoninen edustaja on 3/7.

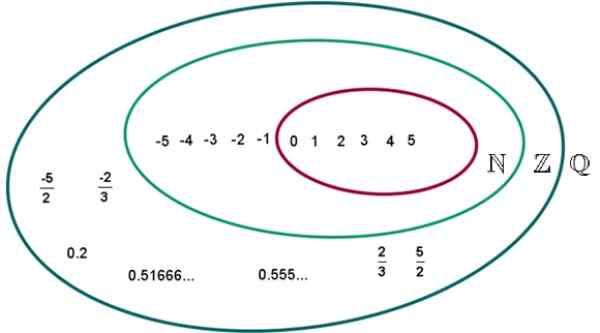Kuva 2.- Q -sarja rationaalisia lukuja. Lähde: Wikimedia Commons. UVM Eduardo Artur/CC BY-S (https: // creativecommons.Org/lisenssit/by-SA/4.0).

Esimerkkejä rationaalisista numeroista

-Omat fraktiot, ne, joissa osoittaja on pienempi kuin nimittäjä:

-Virheelliset fraktiot, joiden numeroija on suurempi kuin nimittäjä:

-Luonnolliset numerot ja kokonaisluvut:

-Vastaavat fraktiot:

Rationaalisen luvun desimaaliohjelmia

Kun osoitin on jaettu nimittäjän kesken on rationaalisen luvun desimaalimuoto. Esimerkiksi:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111 ..

6/11 = 0.545454…

Kahdessa ensimmäisessä esimerkissä desimaalien määrä on rajoitettu. Tämä tarkoittaa, että kun divisioona tehdään, lepo saadaan.

Toisaalta kahdessa kahdessa desimaalien lukumäärä on ääretön, ja siksi suspensiot asetetaan. Jälkimmäisessä tapauksessa desimaalissa on kuvio. Fraktion 1/9 tapauksessa kuva 1 toistetaan määräämättömäksi ajaksi, kun taas 6/11 se on 54.

Se voi palvella sinua: Taajuuden todennäköisyys: Konsepti, miten se lasketaan ja esimerkkejä

Kun näin tapahtuu

Muuta desimaali murto -osaksi

Jos se on rajoitettu desimaali, pilkku yksinkertaisesti eliminoidaan ja nimittäjästä tulee yksikkö, jota seuraa niin monta nollaa kuin luvuilla on desimaali. Esimerkiksi desimaalin 1 muuttaminen 1.26 Fraktiossa se on kirjoitettu näin:

1.26 = 126/100

Sitten tuloksena oleva fraktio yksinkertaistetaan maksimiin:

126/100 = 63/50

Jos desimaali on rajoittamaton ensin, ajanjakso tunnistetaan. Sitten näitä vaiheita noudatetaan tuloksena olevan osan löytämiseksi:

-Osoittaja on vähennysluku (ei koomaa tai ympäryssuojaa) ja osaa, joka ei kuljeta ympyrän aksenttia.

-Nimittäjä on kokonaisluku, jolla on niin monta 9 kuin kuviot, jotka ovat ympärysfleksin alla, ja niin monta tai kuin desimaaliosan lukuja, ne eivät ole kehän alla.

Noudatamme tätä menettelyä desimaalin lukumäärän 0,428428428 muuttamiseksi murto -osassa.

-Ensinnäkin ajanjakso tunnistetaan, mikä on toistuva sekvenssi: 428.

-Sitten numeron vähentäminen ilman koomaa tai aksentti on tehty: 0428 osasta, jolla ei ole kehämuotoa, joka on 0. Tämä on 428 - 0 = 428.

-Nimittäjä on rakennettu, tietäen, että kehän alla on 3 lukua ja kaikki ovat kehän alla. Siksi nimittäjä on 999.

-Lopuksi fraktio muodostuu ja yksinkertaistetaan, jos mahdollista:

0 -.428 = 428/999

Ei ole mahdollista yksinkertaistaa enemmän.

Rationaaliset numerot

- Lisää ja vähennä

Fraktiot samalla nimittäjällä

Kun fraktioilla on sama nimittäjä, lisää ne ja/tai vähennä ne ovat erittäin helppoja, koska numeroita lisätään yksinkertaisesti algebrallisesti, jättäen tuloksen nimittäjänä samaan lisäyksiin. Lopuksi, jos mahdollista, sitä yksinkertaistetaan.

Esimerkki

Suorita seuraava algebrallinen summa ja yksinkertaista tulosta:

Tuloksena oleva osuus on jo peruuttamaton.

Fraktiot eri nimittäjän kanssa

Tässä tapauksessa lisäosat korvataan vastaavilla fraktioilla samalla nimittäjällä ja sitten menettely on jo kuvattu. 

Esimerkki

Lisää algebrallisesti seuraavat rationaaliset numerot, jotka yksinkertaistavat tulosta:

Voi palvella sinua: kuution reunat

Vaiheet ovat:

-Määritä nimittäjien 5, 8 ja 3 yleinen monimuotoisuus (MCM):

MCM (5,8,3) = 120

Tämä on tuloksena olevan fraktion nimittäjä yksinkertaistamatta.

-Jokaiselle fraktiolle: Jaa MCM nimittäjän välillä ja kerro numeroijalla. Tämän operaation tulos on asetettu vastaavalla merkinnällä murto -osastoon. Tällä tavoin saadaan murto -osa, joka vastaa alkuperäistä, mutta MCM: n nimittäjänä.

Esimerkiksi ensimmäiselle fraktiolle numeroija on rakennettu näin: (120/5) x 4 = 96 ja saadaan:

Jatka samalla tavalla jäljellä oleville fraktioille:

Lopuksi, vastaavat fraktiot korvataan unohtamatta niiden merkkiä ja tehdään numeroijien algebrallinen summa:

(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

- Kertolasku

Kertolasku ja jako suoritetaan alla esitettyjen sääntöjen mukaisesti:

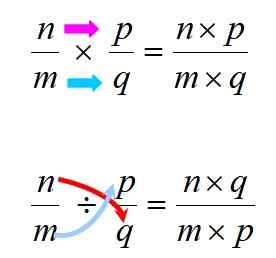Kuva 3. Säännöt rationaalisten lukujen kertolaskennan ja jakamisen toteuttamiseksi. Lähde: f. Zapata.

Joka tapauksessa on tärkeää muistaa, että kertolasku on kommutatiivista, mikä tarkoittaa, että tekijöiden järjestys ei muuta tuotetta. Tätä ei tapahdu divisioonan kanssa, joten sinun on huolehdittava kunnioitusta osinkojen ja jakajan välillä.

Esimerkki 1

Suorita seuraavat toiminnot ja yksinkertaista tulosta:

a) (5/3) x (8/15)

b) (-4/5) ÷ (2/9)

Vastaa

(5/3) x (8/15) = (5 x 8)/(3 x 15) = 15/120 = 1/8

Vastaus b

(-4/5) ÷ (2/9) = (-4 x 9)/(5 x 2) = -36/10 = -18/5

Esimerkki 2     

Luisalla oli 45 dollaria. Hän vietti kymmenennen ostamaan kirjan ja 2/5 osaa siitä, mikä oli jäljellä paitaan. Kuinka paljon rahaa Luisa on jäljellä? Ilmaise tulos peruuttamattomassa osassa.

Ratkaisu

Kirjakustannukset (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $

Siksi Luisa pysyi:

45 - 4.5 $ = 40.5 $

Rahalla Luisa meni vaatekauppaan ja osti paidan, jonka hinta on:

(2/5) x 40.5 $ = 16.2 $

Nyt Luisa on salkussa:

40.5 - 16.2 $ = 24.3 $

Jotta se ilmaista murto -osa, se on kirjoitettu näin:

24.3 = 243/10

Se on peruuttamaton.

Viitteet

1. Baldor, a. 1986. Aritmeettinen. Codex -versiot ja jakaumat.
2. Carena, m. 2019. Matematiikan käsikirja. Rannikon kansallinen yliopisto.
3. Figuera, J. 2000. Matematiikka 8. Co-bo-painikkeet.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Rationaaliset numerot. Toipunut: cimanet.UOC.Edu.
6. Rationaaliset numerot. Haettu: WebDelprofesor.Ula.mennä.