Real numeroita historia, esimerkit, ominaisuudet, toiminnot

Se todelliset numerot Ne muodostavat numeerisen joukon, joka kattaa luonnolliset lukumäärät, kokonaisluvut, rationaaliset ja irrationaaliset. Ne on merkitty symbolilla ℝ tai yksinkertaisesti R - Ja heidän tieteen, tekniikan ja talouden tavoite on sellainen, että puhuttaessa "numerosta" on melkein oletettu, että se on todellinen luku.

Todellisia lukuja on käytetty muinaisista ajoista lähtien, vaikka heille ei annettu sitä nimeä. Siitä hetkestä lähtien, kun Pythagoras kehitti kuuluisan lauseensa, syntyi numeroita, joita ei voitu saada melko luonnollisina luvuina tai kokonaislukuina.

Kuvio 1. Venn -kaavio, joka osoittaa, kuinka reaalilukujoukko sisältää muut numeeriset sarjat. Lähde> Wikimedia Commons.

Esimerkkejä numeroista ovat √2, √3 ja π. Näitä numeroita kutsutaan irrationaalinen, Toisin kuin rationaaliset numerot, jotka tulevat kokonaislukujen välisistä osista. Siksi oli välttämätöntä numeerinen joukko, joka kattaa molemmat numerot.

Termin "reaaliluku" on luonut suuren matemaatikko René Descartes (1596-1650) erottaakseen kahden tyyppiset juuret, jotka voivat johtua polynomiyhtälön ratkaisemisesta.

Jotkut näistä juurista voivat olla negatiivisten lukujen pareja, nämä descartes kutsuivat niitä "kuvitteellisiksi numeroiksi" ja ne, jotka eivät olleet, olivat todellisia lukuja.

Nimitys jatkui ajan myötä, mikä aiheutti kaksi suurta numeerista sarjaa: todelliset numerot ja kompleksilukut, laajempi sarja, joka sisältää todelliset numerot, kuvitteelliset ja ne, jotka ovat todellisessa ja osittain kuvitteellisessa.

Todellisten lukujen kehitys jatkoi kurssiaan vuonna 1872 asti matemaatikko Richard Dedekind (1831-1936) määritelty kaikella muodollisuudella reaalilukujen joukko puheluiden kautta Vaarat Dedekind. Hänen työnsä synteesi lähetettiin artikkeliin, joka näki valon samana vuonna.

Voi palvella sinua: säännölliset monikulmiot: ominaisuudet, elementit, kulmat, esimerkit

[TOC]

Esimerkkejä todellisista numeroista

Seuraava taulukko näyttää esimerkkejä todellisista numeroista. Tämän sarjan alajoukko on luonnollisille lukuille, kokonaislukuille, rationaalisille ja irrationaalisille. Mikä tahansa määrä näitä sarjoja on sinänsä todellinen numero.

Siksi 0, negatiiviset, positiiviset, fraktiot ja desimaalit ovat reaalilukuja.

Kuva 2. Esimerkkejä todellisista numeroista ovat alkuperäiskansojen, kokonaislukut, rationaaliset, irrationaaliset ja transcendentit. Lähde: f. Zapata.

Todellisten lukujen esitys oikealla linjalla 

Todelliset numerot voidaan edustaa oikealla linjalla R -, Kuten kuva näyttää. Ei ole välttämätöntä, että 0 on aina läsnä, mutta on kuitenkin kätevää tietää, että negatiiviset reagit ovat vasemmalla ja oikealla positiivisella tavalla. Siksi se on erinomainen vertailupiste.

Oikealla linjalla A -asteikko otetaan, josta kokonaisluvut löytyvät:… 3, -2, -1, 1, 2, 3… . Nuoli osoittaa, että viiva ulottuu äärettömyyteen. Mutta se ei ole kaikki, millään tavalla tarkasteltuna löydämme aina äärettömiä todellisia lukuja.

Todelliset numerot on esitetty järjestyksessä. Aluksi on olemassa kokonaislukujen järjestys, jossa positiivinen.

Tämä tilaus pysyy todellisissa numerossa. Seuraavat eriarvoisuudet esitetään esimerkkinä:

a) -1/2 < √2

b) e < π

c) π> -1/2

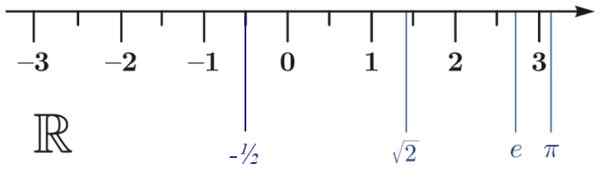Kuva 3.- Todellinen linja. Lähde: Wikimedia Commons.

Todellisten lukujen ominaisuudet

-Todelliset numerot sisältävät luonnolliset numerot, kokonaisluvut, rationaalinen ja irrationaalinen.

Voi palvella sinua: Mitkä ovat kolmionumerot? Ominaisuudet ja mielenosoitukset

-Summan kommutatiivinen ominaisuus toteutetaan: Lisäysjärjestys ei muuta summaa. Jos A ja B ovat kaksi todellista numeroa, on aina totta, että:

A + B = B + A

-0 on summan neutraali elementti: a + 0 = a

-Assosiatiivinen omaisuus täyttyy summalle. Jos a, b ja c ovat todellisia numeroita: (a + b) + c = a + (b + c).

-Todellisen numeron A vastakohta on -a.

-Vähennys määritellään päinvastaisen summana: a - b = a + (-b).

-Tuotteen kommutatiivinen ominaisuus toteutetaan: tekijöiden järjestys ei muuta tuotetta: a.B = b.-lla

-Assosiatiivinen ominaisuus sovelletaan myös tuotteeseen: (a.b).C = a.(b.c)

-1 on kertolaskujen neutraali elementti: a.1 = a

-Kertolaskennan jakautuva ominaisuus lisäyksen suhteen on voimassa: a. (b+c) = a.b + a.c

-Jaostoa 0: lla ei ole määritelty.

-Minkä tahansa todellisen numeron A, paitsi 0, on moninkertainen käänteinen^-1 sellainen, että a.-lla^-1 = 1.

-Jos a on todellinen numero: a^{0 -} = 1 ja a¹ = a.

-Todellisen numeron absoluuttinen arvo tai moduuli on etäisyys mainittujen lukujen ja 0: n välillä.

Toiminnot reaalilukujen kanssa

Todellisten lukujen avulla voit tehdä operaatioita, jotka on tehty muilla numeerisilla sarjoilla, mukaan lukien summa, vähennys, kertolasku, jako, parannus, säteily, logaritmit ja paljon muuta.

Kuten aina, jakautumista 0: lla ei ole määritelty, negatiivisten lukujen tai 0: n logaritmeja ei ole myöskään, vaikka on totta, että log 1 = 0 ja että lukujen logaritmit välillä 0 ja 1 ovat negatiivisia.

Sovellukset

Real -lukujen sovellukset kaikenlaisiin tilanteisiin ovat erittäin monipuolisia. Todelliset luvut ilmestyvät moniin ongelmiin tarkkoissa tieteissä, tietokoneissa, tekniikassa, taloudessa ja yhteiskuntatieteissä.

Se voi palvella sinua: Hipparco of Niza: Elämäkerta ja panos tieteeseen

Kaikenlaiset suuruudet ja määrät, kuten etäisyydet, ajat, voimat, äänenvoimakkuus, raha ja monet muut, ilmaisee reaalilukuina.

Puhelinsignaalien, videon kuva ja ääni, ilmastoinnin lämpötilaa, lämmitin tai jääkaappia voidaan ohjata digitaalisesti, mikä tarkoittaa fyysisten suuruuksien muuttamista numeerisiksi sekvensseiksi.

Sama tapahtuu, kun pankkitapahtuma tehdään verkossa tai pikaviestejä. Todelliset numerot ovat kaikkialla.

Liikuntaa

Katsotaanpa harjoituksilla, kuinka nämä numerot toimivat yhteisiä tilanteita, joiden kanssa olemme päivittäin.

Harjoitus 1

Postitoimisto hyväksyy vain paketit, joille pituus plus muodon mittaus ei ylitä 108 tuumaa. Siksi on täytettävä, että paketti on hyväksytty, että:

L + 2 (x + y) ≤ 108

a) Ohitatko paketin, joka mittaa 6 tuumaa leveä, 8 tuumaa pitkä ja 5 jalkaa pitkä?

b) Entä sellainen, joka mittaa 2 x 2 x 4 jalkaa³?

c) Mikä on korkein hyväksyttävä paketille, jonka pohja on neliö ja mittaa 9 x 9 tuumaa²?

Vastaa

L = 5 jalkaa = 60 tuumaa

x = 6 tuumaa

y = 8 tuumaa

Ratkaistava toiminta on:

L + 2 (x + y) = 60 + 2 (6 + 8) tuumaa = 60 + 2 x 14 tuumaa = 60 + 28 tuumaa = 88 tuumaa

Paketti hyväksytään.

Vastaus b

Tämän paketin mitat ovat alhaisemmat kuin paketin a), joten molemmat onnistuvat ohittamaan.

Vastaus C

Tässä paketissa:

x = l = 9 tuumaa

Se on täytettävä, että:

9+ 2 (9+ y) ≤ 108

27 + 2y ≤ 108

2y ≤ 81

ja ≤ 40.5 tuumaa

Viitteet

1. Carena, m. 2019. Preuniversity -matematiikan käsikirja. Rannikon kansallinen yliopisto.
2. Diego, a. Todelliset numerot ja niiden ominaisuudet. Toipunut: matematiikka.ENSIMMÄ.Edu.AR.
3. Figuera, J. 2000. 9. matematiikka. Aste. Co-bo-painikkeet.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.