Transsendenttiset numerot, jotka ovat kaavoja, esimerkkejä, harjoituksia

Se transcendent numerot He ovat niitä, joita ei voida saada polynomiyhtälön seurauksena. Transsendenttisen numeron vastakohta on a algebrallinen numero, jotka ovat tyypin polynomiyhtälön ratkaisuja:

-lla_n xⁿ + -lla_N-1 x^N-1 +… + A₂ x² + -lla₁ x + a_{0 -} = 0

Missä kertoimet_n, -lla_N-1,…₂, -lla₁, -lla_{0 -} Ne ovat rationaalisia lukuja, nimeltään polynomikertoimet. Jos X -numero on ratkaisu edelliselle yhtälölle, tämä luku ei ole transsendentti.

Kuvio 1. Kaksi suurta merkitystä tieteessä ovat transsendenttisia lukuja. Lähde: Julkiset alueet.netto.

Analysoimme muutamia numeroita ja katsomme, ovatko ne transsendentteja:

a) 3 ei ole transsendentti, koska se on x - 3 = 0 ratkaisu.

b) -2 ei voi olla transsendentti, koska se on x + 2 = 0: n ratkaisu.

c) ⅓ Se on 3x - 1 = 0 ratkaisu

d) Yhtälön X ratkaisu² - 2x + 1 = 0 on √2 -1, joten mainittu lukumäärä määritelmän mukaan ei ole transsendentti.

e) ei myöskään √2, koska se on yhtälön x tulos² - 2 = 0. Nostamalla √2 -neliö, se johtaa 2: een, joka vähennetään 2: sta, ei ole merkitystä nollaan. Joten √2 on irrationaalinen luku, mutta se ei ole transsendentti.

[TOC]

Mitkä ovat transsendenttiset numerot?

Ongelmana on, että niiden hankkimiseksi ei ole yleistä sääntöä (myöhemmin sanomme lomakkeen), mutta jotkut tunnetuimmista ovat numero pilli ja Neperin numero, merkitty vastaavasti: π ja ja.

Numero π

Numero π Luonnollisesti näyttää tarkkailemassa, että matemaattinen osuus ympyrän kehän P ja sen halkaisija d välillä riippumatta siitä, onko se pieni vai suuri ympyrä, antaa aina saman määrän, nimeltään pilli-

π = P/d ≈ 3 14159…

Tämä tarkoittaa, että jos kehän halkaisija pidetään mittayksikkönä, kaikille, olipa ne suuria tai pieniä, kehä on aina arvoinen p = 3,14… = π, Kuten kuvan 2 animaatiossa voidaan nähdä.

Voi palvella sinua: Bolzano -lause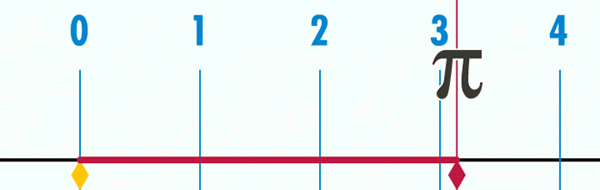Kuva 2. Ympyrän kehän pituus on joskus halkaisijan pituus, joka on noin 3,1416.

Lisää desimaalien määrittämiseksi sinun on mitattava tarkempi P ja D. Johtopäätös on, että osamäärän desimaaleilla ei ole loppua eikä niitä koskaan toisteta, joten numero π Sen lisäksi, että se on transsendentti, se on myös irrationaalinen.

Irrationaalinen numero on se luku, jota ei voida ilmaista kahden kokonaisluvun jakautumisena. 

On tiedossa, että jokainen transsendenttinen luku on irrationaalista, mutta ei ole totta, että kaikki irrationaaliset ovat transsendentteja. Esimerkiksi √2 on irrationaalinen, mutta se ei ole transsendentti.

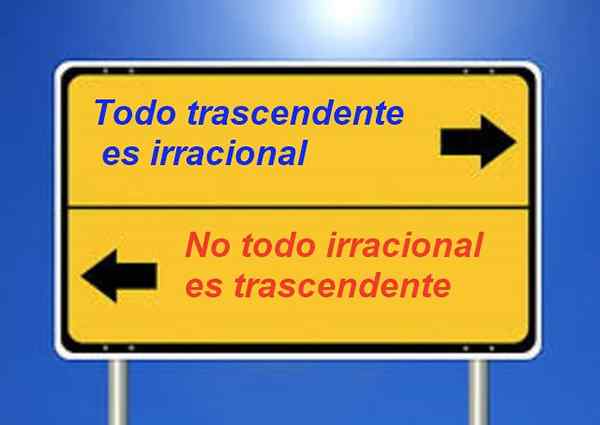Kuva 3. Transsendenttiset numerot ovat irrationaalisia, mutta vastavuoroinen lausunto ei ole totta.

Numero E

Transsendenttinen luku on Neperian logaritmien perusta ja niiden desimaalimyrsky on:

e ≈ 2.718281828459045235360… .

Jos haluat kirjoittaa numeron ja Tarkalleen ottaen olisi tarpeen kirjoittaa desimaalin ääretön, koska jokainen transsendentti luku on irrationaalista, kuten aiemmin sanottu.

Ensimmäiset kymmenen numeroa ja Ne on helppo muistaa:

2,7 1828 1828 ja vaikka se näyttää noudattavan toistuvaa mallia, sitä ei saavuteta yli yhdeksän järjestyksen desimaaleissa.

Muodollisempi määritelmä ja on seuraava:

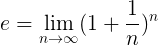
Mikä tarkoittaa, että tarkka arvo ja Tässä kaavassa ilmoitettu toiminta saavutetaan, kun luonnollinen luku n Sillä on taipumus äärettömyys.

Tämä selittää miksi voimme vain saada lähestymistapoja ja, Koska suuri numero n on sijoitettu, voit aina löytää a n vanhukset.

Etsitään joitain lähestymistapoja yksin:

-Kun n = 100 sitten (1 + 1/100)¹⁰⁰ = 2 70481, joka tuskin tapahtuu ensimmäisessä desimaalissa E: n "tosi" -arvon kanssa.

-Jos sinut valitaan n = 10.000 Sinulla on (1 + 1/10.000)^10.000 = 2 71815, joka vastaa E: n ”tarkan” arvoa kolmen ensimmäisen desimaalin aikana.

Voi palvella sinua: homologiset puolet

Tätä prosessia tulisi noudattaa voidakseen saada E: n "todellinen" arvo. En usko, että meillä on aikaa saavuttaa se, mutta tehdään vielä yksi yritys:

Käytetään n = 100.000:

(1 + 1/100.000)^100.000 = 2,7182682372

Että sillä on vain neljä desimaalia, jotka ovat samat kuin arvokkaita arvoja.

Tärkeää on ymmärtää, että mitä suurempi N -arvon arvo on laskemaan ja_n, Lähempänä on todellinen arvo. Mutta tämä todellinen arvo pidetään vasta, kun n on ääretön.

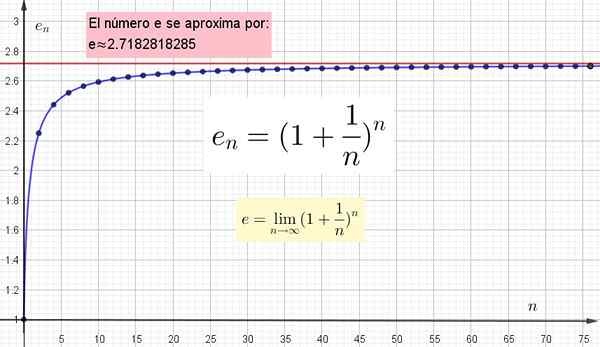Kuva 4. Se on graafisesti esitetty, koska N: n korkeampi arvo on lähempänä E: tä, mutta tarkan arvon saavuttamiseksi n on oltava ääretön.

Muut transsendenttiset numerot

Näiden kuuluisten lukujen lisäksi on esimerkiksi muita transsendenttisia numeroita:

- 2^√2

Mikä tahansa algebrallinen lukumäärä, joka ei ole 0 tai 1, nostettu irrationaaliseen eksponenttiin, on transsendenttinen luku.

-Champernownen numero 10: 

C_10 = 0,123456789101112131415161718192021… .

-Champernownen numero 2:

C_2 = 0,110111001011011… .

-Euler-Mascheroni-γ tai vakio gamma-luku:

γ ≈ 0,577 215 664 901 532 860 606

Se saadaan tekemällä seuraava laskelma:

γ ≈ 1 + ½ + ⅓ + ¼ +… + 1/n - ln (n)

Kun n olla erittäin iso. Gamma -numeron tarkan arvon saamiseksi on tarpeen laskea n ääretön. Jotain samanlaista kuin mitä teimme yllä.

Ja transsendenttisia lukuja on paljon enemmän. Venäjällä syntynyt ja vuosina 1845–1918 syntynyt suuri matemaatikko Georg Cantor osoitti, että transsendenttisten lukujen joukko on paljon suurempi kuin algebralliset luvut.

Kaavat, joissa transcendent -numero π ilmestyy

Kehän kehä

P = π d = 2 π r, missä p on kehä, D -halkaisija ja r ympärysmiehen säde. On muistettava, että:

Voi palvella sinua: kuinka paljon sinun on lisättävä 3/4 saadaksesi 6/7?

-Ympyrän halkaisija on pisin segmentti, joka yhdistää sen kaksi pistettä ja joka kulkee aina keskuksensa läpi,

-Säde on puolet halkaisijasta ja segmentti, joka menee keskustasta reunaan.

Ympyräalue

A = π r² = ¼ π d²

Pallon pinta

S = 4 π r^2.

Joo. Vaikka se ei näytä, pallon pinta on sama kuin saman säteen neljän ympyrän pinta.

Pallon tilavuus

V = 4/3 π r³

Harjoitukset

- Harjoitus 1

"Eksoottinen" pizzeria myy kolme halkaisijaltaan pizzaa: 30 cm pieni, mediaani 37 cm ja iso 45 cm. Lapsi on erittäin nälkäinen ja tajusi, että kahdella pienellä pizzalla on sama kustannus kuin suurella. Mikä on hänelle parempi, osta kaksi pientä pizzaa tai suurta?

Kuva 5.- Pizzan pinta -ala on verrannollinen säteen neliöön, mikä on suhteellisuusvakio. Lähde: Pixabay.

Ratkaisu

Mitä suurempi alue, sitä suurempi pizzan määrä, tästä syystä suuren pizzan pinta -ala lasketaan ja verrataan kahteen pieneen pizzaan:

Suuri pizza -alue = ¼ π d² = ¼ ⋅3 1416⋅45² = 1590,44 cm²

Pieni pizza -alue = ¼ π d² = ¼ ⋅3 1416⋅30² = 706,86 cm²

Siksi kahdella pienellä pizzalla on alue 

2 x 706,86 = 1413,72 cm² .

On selvää: Pizzaa ostaa enemmän suuria kuin kaksi pientä.

- Harjoitus 2

"Eksoottinen" pizzeria myy myös 30 cm: n säde semi -man -pizzalle samalla suorakulmaisella muodossa 30 x 40 cm puolella. Kumman valitsisit?

Kuva 6.- Puoli -etsijän pinta on kaksinkertainen pohjan pyöreä pinta. Lähde: f. Zapata.

Ratkaisu

Kuten edellisessä osassa todetaan, pallon pinta on neljä kertaa suurempi kuin saman halkaisijan ympyrän, joten halkaisija 30 cm: n puolivälissä on:

30 cm puoliksi -man -pizza: 1413,72 cm² (kahdesti pyöreä sama halkaisija)

Suorakulmainen pizza: (30 cm) x (40 cm) = 1200 cm² .

Semi -man -pizzalla on suurempi alue.

Viitteet

1. Fernández J. Numero E. Alkuperä ja uteliaisuus. Toipunut: soijamatematiikka.com
2. Nauti matematiikasta. Eulerin numero. Toipunut.com.
3. Figuera, J. 2000. 1. matematiikka. Monipuolinen. Co-bo-painikkeet.
4. Garcia, m. Alkuperäisen laskelman numero E. Toipunut: matematiikka.Kisat.UCV.mennä.
5. Wikipedia. Pi -numero. Toipunut: Wikipedia.com
6. Wikipedia. Transcendent numerot. Toipunut: Wikipedia.com