Desimaali

Desimaalissa kirjoitettu 3/2 -osa

Mikä on desimaalimerkintä?

Se desimaali Se koostuu todellisen numeron kirjoittamisesta kokonaisen osan ja desimaaliosan kautta, molemmat erotetaan pisteellä tai pilkulla. Koko osa on vasemmalle ja desimaaliosa kyseisen pisteen oikealla puolella.

0 voi näkyä sekä koko osassa että desimaalissa. Esimerkiksi seuraavat luvut ovat desimaalilukuja:

• 0 -.25
• 1.5903
• 4 19367

Huomaa, että näiden lukujen desimaaliosa on rajallinen, mutta on myös numeroita, joissa on ääretön desimaaliosa, kuten 0,333333…, missä rivittävät kohdat asetetaan keinona osoittaa, että desimaalien lukumäärä jatkuu loputtomiin.

Yleensä rajallinen desimaalin lukumäärä voidaan kirjoittaa seuraavasti:

N.-lla₁-lla₂-lla₃…_n

Koska desimaalien määrä on kokonaisluku, kun taas ääretön desimaali ottaa lomakkeen:

N.-lla₁-lla₂-lla₃..

Desimaalissa 0.25 tunnistetaan:

• N = 0
• -lla₁ = 2
• -lla₂ = 5

Desimaalit syntyvät toisena tapana ilmaista rationaalisia lukuja, jotka ovat muotoisia tai rikki. Itse asiassa mikä tahansa murto -osa voidaan kirjoittaa desimaalimerkinnässä, kuten heti nähdään.

Ne edustavat myös numeroita, jotka eivät johdu murto -osasta, niin nimeltään irrationaaliset numerot, kuten: π, √2, √3, √5, numero "E" ja monet muut.

Esimerkkejä desimaalilukuista

Desimaalin lukumäärä voidaan saada murto -osasta hyvin yksinkertaisella tavalla: Nimittäjän välisen osamäärän laskeminen nimittäjän välillä. Jos nimittäjä on yksikkö, jota seuraa nolla, tämä on hyvin yksinkertaista:

• 8/10 = 0.8
• - (5/100) = −0.05

Ensimmäisessä tapauksessa, koska nimittäjä on 10, desimaalin tarkkuudella asetetaan välittömästi 8: n ja desimaalin 0 vasemmalle puolelle.8 lukee "8 kymmenesosaa" tai "nollapiste kahdeksan".

Toisessa tapauksessa, koska nimittäjä on 100, sinun on asetettava desimaalipiste kaksi paikkaa vasemmalle viidestä, ja koska luku on negatiivinen, se lukee "vähemmän 5 sataa" tai "vähemmän nolla nollapiste viisi".

Kun nimittäjä ei ole yksikkö, jota seuraa 0, käytetään pitkää jakoa:

Huomaa, että tämän jaon toteuttamiseksi, koska numeraattori on pienempi kuin nimittäjä, se moninkertaistettiin ensin 10: llä, ja sen tekemisessä 0 seurasi osamäärän desimaalipiste, jotta toimenpide ei muuttaisi, niin että ei Operaation muuttaminen. Jatka sitten normaalisti jakamaan 10 2: lla, joka on yhtä suuri kuin 5 ja jakojäämä on 0.

Voi palvella sinua: vektorimäärät

Fraktion desimaalimuoto ½ on 0.5, "nollapiste viisi" luetaan:

Jake 7/8 on toinen esimerkki. Koska 7 on alle 8, se moninkertaistaa 7 × 10 = 70, 0 asetetaan osamäärään, jota seuraa desimaalipiste ja jaetaan yleensä:

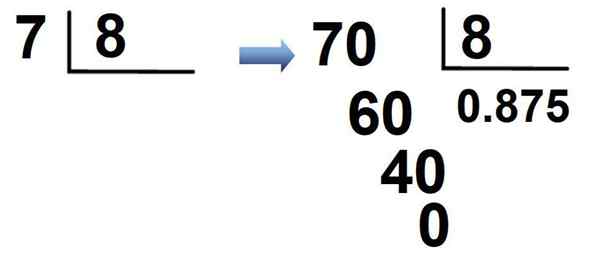
Tuloksena on, että murto on kirjoitettu desimaalimerkinnässä kuten:

7/8 = 0.875

Tämä luku, kuten edellinen tulos, on rajallinen desimaali ja tapa lukea se on: "nollapiste kahdeksansataa seitsemänkymmentä -viisi". Tämän menettelyn avulla seuraavat fraktiot on kirjoitettu myös desimaalimerkinnässä:

8/10 = 0.8

5/7 = 0.714285714…

9/20 = 0.Neljä viisi

3/8 = 0.375

Huomaa, että kuten kaikissa näissä fraktioissa, numeroija on pienempi kuin nimittäjä, tuloksena olevien desimaalien koko osa on 0. Sekoitettu luku tai a Virheellinen osuus (Sillä, jonka numeroija on suurempi kuin sen nimittäjä) on myös desimaalin esitys.

Tässä tapauksessa koko osa on suurempi tai yhtä suuri kuin 1, jos murto on positiivinen ja alle -1, jos se on negatiivinen:

9/4 = 2.25

10/3 = 3.333333…

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Koko osa ja murto -osa negatiivisista desimaaleista

Edellisissä esimerkeissä havaittiin, että murto -osan desimaalin ilmaisun löytämiseksi osoittaja ja nimittäjä on yksinkertaisesti jaettu. Vaikka murto on negatiivinen, yksinkertaisesti miinusmerkki asetetaan vastaavaan desimifiseen lausekkeeseen.

Koko osa ja desimaalin murtoosa eroavat kuitenkin kuljettamasi merkin mukaan.

Kun desimaali on positiivinen, kuten 2.25, sen koko osa on 2 ja sen desimaaliosa on 0.25 ja luku voidaan kirjoittaa koko osan ja desimaalin osien summana, kuten tämä:

2.25 = 2 + 0.25

Koko osa määritellään kokonaislukuksi, joka on välittömästi alhaisempi kuin desimaalit ja desimaaliosa on aina positiivinen. 2.25, heti alempi kokonaisluku on 2.

Mutta fraktiossa −12/5, vastaa desimaalia −2.4 Yllä oleva ei toimi.

Voi palvella sinua: mitkä ovat Cartesian lentokoneen osat?

 Jos −2, se oli koko osa ja 0.4 saadaan desimaaliosa lisäämällä:

−2 + 0.4 = −1.6 ≠ −2.4

Siksi koko −2: n osa.4 ei voi olla −2, mutta heti alempi kokonaisluku: −3. Mutta siinä tapauksessa murto -osa ei olisi 0.4, koska lisäämällä:

−3 + 0.4 = −2.6 ≠ −2.4

Joten mikä on negatiivisen luvun –2 desimaaliosa.4? Se vähentää desimaalin lukumäärää koko osastaan ​​ja tulos on aina positiivinen:

−2.4 - ( - 3) = 0.6

Lopuksi on todistettu, että lisäämällä koko osa ja murto -osa, saadaan desimaali:

−3 + 0.6 = −2.4

Menettely, joka löytyy kokonaisen osan ja desimaaliosasta minkä tahansa määrän merkistä riippumatta, on tiivistetty tällä tavalla:

• Koko osa on kokonaisluku, joka on heti alhaisempi kuin desimaaliluku.
• Desimaaliosa lasketaan vähentämällä desimaali koko osastaan.

Käytännön laskentatarkoituksiin desimaaliluku −2.4 voidaan hajottaa nimellä - (2 + 0.4) = - 24/10 tai:

Kuten voidaan nähdä, lukumäärän desimaalimerkinnän esitys ei ole ainutlaatuinen.

Desimaalityypit

On desimaalilukuja, joiden desimaaliosa on rajallinen tai ääretön, jota käytetään luokituskriteerinä:

Rajallinen tai tarkka desimaali

Kun desimaalit ovat rajallisia, kuten 0.125, sanotaan myös, että he ovat tarkat desimaalit.

Ääretön desimaali

Ääretön desimaali saadaan, kun osoiton ja nimittäjän välisen jaon jäännökset eivät koskaan tee 0.

Edellyttäen, että desimaali tulee kahden kokonaisluvun välisestä osamäärästä, tämä desimaaliosa on jaksollinen, ts. Se koostuu yhdestä tai useammasta luvusta, joita toistetaan toistaiseksi, nimeltään ajanjakso.

Esimerkiksi numero 3.333333 ... Tätä voidaan symboloida asettamalla käyrä tai hattu toistuvaan numeroon:

Jakso voi olla suurempi luku, kuten fraktiossa 5/7, jonka esitys desimaalimerkinnässä on 0.71428571428571428… ja se on kirjoitettu seuraavasti:

Voi palvella sinua: suhteellinen variaatio

Näitä desimaaleja, joissa ajanjakso ilmestyy heti desimaalin jälkeen Puhdas säännölliset desimaalit. Tässä toisessa:

Jaksoa, joka on 45, edeltää kaksi numeroa, joita ei enää toisteta desimaaliosassa: 23. Tätä lukua kutsutaan ante-jakso, Koska se edeltää ajanjaksoa. Tässä tapauksessa se on a Sekoitettu sanomalehti desimaali.

Viimeinkin on äärettömiä desimaaleja, jotka eivät ole sanomalehtiä, jotka eivät ole peräisin kahden kokonaisluvun välisestä osuudesta. Kuten alussa mainittiin, nämä desimaalit kuuluvat kokonaisuuteen irrationaaliset numerot, Kuten esimerkiksi PI -numero.

Ratkaisut

Harjoitus 1

Kirjoita numeerinen seuraavat desimaalilukut:

a) nollapiste neljäsataa neljäkymmentäseitsemästä
b) Viisi tuhannesosaa
c) Kaksi yksikköä ja viisi sataa
d) Kolme pistettä kaksikymmentäseitsemän negatiivista
e) Yksi piste kahdeksataa kaksikymmentätuhatta viisisataa kuusikymmentä -kolme

• Ratkaisu

a) 0.447

b) 0.005

c) 2.05

d) −3.27

e) 1.824563

Harjoitus 2

Luokittelee seuraavat desimaalilukut tarkkaan desimaaliin, puhtaisiin sanomalehtiin, sekoitettuihin sanomalehtiin tai irrationaalisiin lukuihin. Kaikissa tapauksissa ilmoita koko osan arvo, ja jos ne ovat sanomalehtiä tai sekoitettuja sanomalehtiä, ilmoita myös ajanjakson ja etuosan arvon, tarvittaessa:

a) 0.35627

b) 1.21212121…

c) −1.32

d) 1.414213562… = √2

• Ratkaisu

a) 35627 on tarkka desimaali. Sen koko osa on 0 ja sen desimaalin osa on 0.35627.

b) 1.21212121… on ääretön desimaali ja puhdas sanomalehti, koko osa on 1 ja ajanjakso 21.

c) −1.32 on tarkka ja negatiivinen desimaali, jonka koko osa on −2. Desimaaliosa lasketaan vähentämällä desimaalin lukumäärä koko osasta:

−1.32 - (−2) = 0.68

d) √2: n desimaalimyrsky on ääretön eikä ole määräajoin, koska se on irrationaalinen luku.

Se on sekoitettu sanomalehti, koko osa on 3, etuosa on 1 ja ajanjakso on 89.

Viitteet

1. Pedagoginen panos ja didaktinen materiaali. Desimaali. Toipunut: Tecdigital.TEC.Ac.Cr.
2. Baldor, a. 2007. Käytännöllinen teoreettinen aritmeettinen. Toimitusryhmä Patria S.-Lla. C: n.V.
3. Matematiikka kaupalle. Desimaalin ymmärtäminen. Haettu osoitteesta: OpenTextbc.Ac.
4. Yksinäinen. Järkevä lukumäärä: Merkitykset ja esitykset. Palautettu: redi.Koodi-.Yksinäinen.MX.