Ohm -vastus, esimerkit ja liikuntatoimenpiteet ratkaistu

Hän ohmi U ohmio on kansainväliseen yksikköjärjestelmään kuuluva sähkövastuksen yksikkö (SI), jota käytetään laajasti tieteessä ja tekniikassa. Tämä nimitettiin saksalaisen fyysikon Georg Simon Ohmin (1789-1854) kunniaksi.

Ohm oli Münchenin yliopiston professori ja tutkija, ja hänen monien panoksensa sähkön ja magneettisuuden määritelmä on resistenssin määritelmä jännitteen ja kuljettajan läpi kulkevan virran välillä. 

Kuvio 1. Monimuotoiset vastukset, jotka muodostavat osan piiristä. Lähde: Wikimedia Commons.

Tämä suhde tunnetaan nimellä Ohmin laki ja se ilmaistaan ​​yleensä seuraavasti: 

R = Δv/i

Jos R edustaa sähkövastusta, ΔV on jännitteet voltissa (v) ja i on virran ampeissa (a), kaikki yksiköissä, jos.

Siksi 1 ohmi, joka on myös merkitty vuorottelevasti kreikkalaisen kirjaimen ω kanssa, on yhtä suuri kuin 1 v/a. Se tarkoittaa, että jos 1 V: n jännitteen luominen tietyn kuljettajan kautta, se aiheuttaa virran 1 A, mainitun kuljettajan vastus on 1 Ω.

Sähkövastus on hyvin yleinen piirielementti, jota käytetään monin tavoin virran oikein hallitsemiseksi riippumatta siitä, onko se osa integroitua tai erikseen.

[TOC]

Sähkövastuksen mittaus

Kuva 5. Georg Simon Ohm, jonka nimi on vastusyksikkö, syntyi Baijerissa vuonna 1789 ja antoi suuren panoksen sähköän, akustiikkaan ja valon aaltojen häiriöihin. Lähde: Wikimedia Commons.

Resistanssit mitataan monimittarin, mittarin avulla, joka tulee analogisina ja digitaalisina versioina. Eniten perusteet mittaavat suoria jännitteitä ja virtauksia, mutta lisätoiminnoilla on enemmän hienostuneita laitteita. Kun niitä käytetään resistenssin mittaamiseen, niitä kutsutaan ohmimetreiksi tai ohmimetriksi. Tätä laitetta on hyvin helppo käyttää:

Voi palvella sinua: Poisson -kerroin: Kerroin, kaavat, arvot, esimerkit

- Keskusvalitsin asetetaan vastuskyvyn mittaamiseen, valitsemalla yhden ω -symbolin tunnistetuista asteikoista, jos instrumentissa on enemmän kuin yksi enemmän kuin yksi.

- Mittausvastus uutetaan piiristä. Jos se ei ole mahdollista, virtalähde on tarpeen pois päältä.

- Instrumentin kärjen tai koettimien välinen vastus on sijoitettu. Polaarisuudella ei ole merkitystä.

- Arvo luetaan suoraan digitaalisella näytöllä. Jos instrumentti on analoginen, sillä on merkitty asteikko ω -symbolilla, joka luetaan oikealta vasemmalle.

Seuraavassa kuvassa (numero 2) esitetään digitaalinen yleismittari ja sen koettimet tai kärkit. Mallissa on vain yksi asteikko resistenssin mittaamiseksi, osoitettuna nuolella.

Kuva 2. Digitaalinen yleismittari. Lähde: Pixabay.

Usein kaupallisen sähkövastuksen arvo ilmaistaan ​​värillisten kaistojen koodilla ulkomailla. Esimerkiksi kuvion 1 vastuksissa on punainen, violetti, kulta, keltainen ja harmaa nauhat. Jokaisella värillä on numeerinen merkitys, joka osoittaa nimellisarvon, kuten sitten näytetään.

Värikoodiresistenssien

Seuraavassa taulukossa värilliset koodit vastusille ilmestyvät:

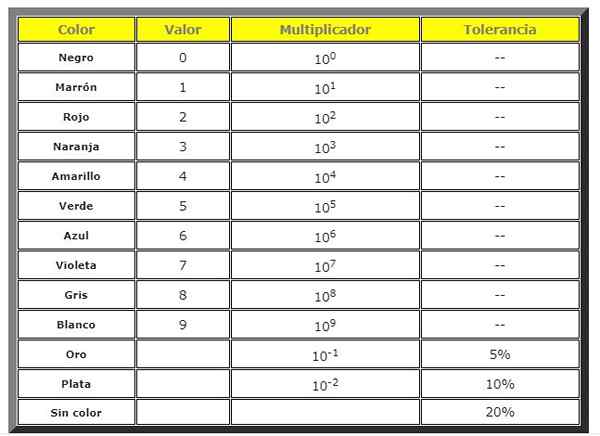pöytä 1.

Kun otetaan huomioon, että metallinen kaista on oikea, koodia käytetään seuraavasti:

- Kaksi ensimmäistä väriä vasemmalta oikealle antavat vastarinnan arvon.

- Kolmas väri osoittaa 10: n tehon, jolla se on kerrottava.

- Ja neljäs osoittaa valmistajan perustaman toleranssin.

Esimerkkejä vastusarvoista

Katsotaanpa esimerkiksi etualalla oleva vastus, kuvan 1 vasemmalla puolella. Näytetty värillinen sekvenssi on: harmaa, punainen, punainen, kulta. Muista, että kulta- tai hopeanauhan on oltava oikea.

Voi palvella sinua: Gauss -laki

Harmaa edustaa 8, punainen on 2, kerroin on punainen ja yhtä suuri kuin 10² = 100 ja lopuksi, toleranssi on kultainen, joka symboloi 5%. Siksi vastus on 82 x 100 Ω = 8200 Ω.

Koska se on 5 %: n toleranssi, se on vastaava ohmissa: 8200 x (5/100) ω = 410 Ω. Siksi vastusarvo on välillä: 8200 - 410 ω = 7790 Ω ja 8200 + 410 ω = 8610 Ω.

Värillisen koodin kautta on nimellinen tai vastustehtaan arvo, mutta toimenpiteen määrittämiseksi on tarpeen mitata vastus yleismittarilla, kuten aiemmin selitetään.

Toinen esimerkki seuraavan kuvan vastuskyvystä:

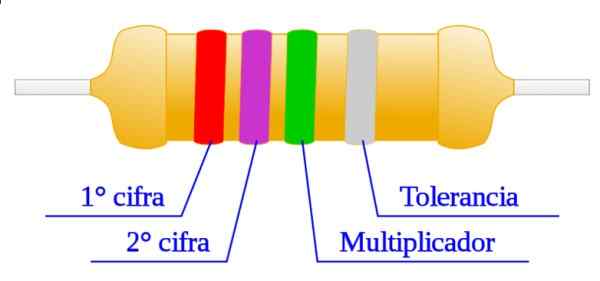Kuva 3. Värikoodin käyttö vastus r. Lähde: Wikimedia Commons.

Meillä on seuraava vastus R: punainen (= 2), violetti (= 7), vihreä (kerro 10: llä⁵), joten kuvan vastus on arvoltaan 27 x 10⁵ Ω. Toleranssinauha on hopea: 27 x 10⁵ x (10/100) ω = 27 x 10⁴ Ω. Tapa ilmaista edellinen tulos, pyöristämällä 27 x 10⁴ 30 x 10⁴, On:

R = (27 ± 3) × 10⁵ Ω = (2.7 ± 0.3) × 10⁶ Ω 

Useimmat käytetyt etuliitteet

Arvot, jotka sähkövastuksella voi olla, ovat aina positiivisia, ovat erittäin laajalla alueella. Siksi 10: n voimia käytetään ilmaisemaan arvojaan, samoin kuin etuliitteitä. Seuraavaksi tavallisin:

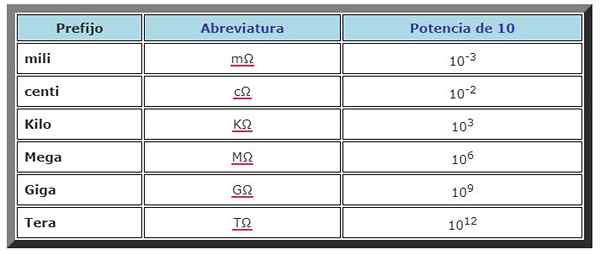Taulukko 2.

Tämän merkinnän mukaan edellisen esimerkin vastus on: (2.7 ± 0.3) MΩ.

Voi palvella sinua: Kohtavuus: kaavat, laskelmat, esimerkit, harjoitukset

Kapelliresistenssi

Reskenssit valmistetaan erilaisista materiaaleista, ja se on vastustaja, joka kuljettajan on kulunut virran, kuten tiedetään, kaikki materiaalit eivät suorita samalla tavalla. Jopa johtimina pidetyissä materiaaleissa on eroja.

Resistenssi riippuu useista ominaisuuksista, mikä on tärkein:

- Kuljettajan geometria: poikkileikkauksen pituus ja pinta -ala.

- Materiaalin resistiivisyys: osoittaa materiaalin esittämän vastustuksen virran kulkemiseen.

- Lämpötila: Resistiivisyys ja vastus nousevat lämpötilan kanssa, koska materiaalin sisäinen järjestelmä pienenee ja siten nykyiset kantajat estävät niiden kulkua.

Jatkuvalle poikkileikkausjohtimelle tietyssä lämpötilassa vastus annetaan:

R = ρ (ℓ/a)

Jos ρ on materiaalin resistiivisyys kyseisessä lämpötilassa, joka määritetään kokeellisesti, ℓ on johtimen pituus ja a on ristien alueiden alue.

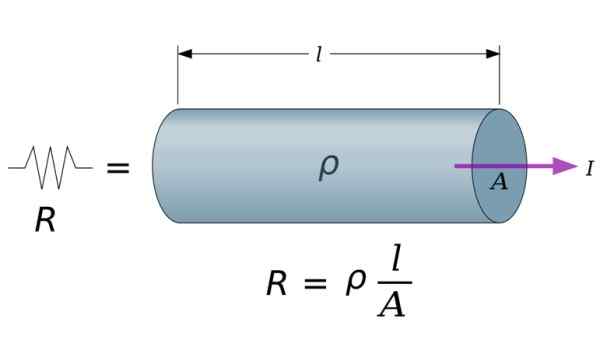Kuva 4. Kapelliresistenssi. Lähde: Wikimedia Commons.

Liikuntaa

Löydä 0 kuparilangan vastus.32 mm säde ja 15 cm pitkä, tietäen, että kupariristillisyys on 1.7 × 10^-8 Ω.m.

Ratkaisu

Koska resistiivisyys on kansainvälisen järjestelmän yksiköissä, sopivin on ilmaista ristikkäinen alue ja näiden yksiköiden pituus ja korvata sitten edellinen osa:

Radio = 0.32 mm = 0.32 × 10^-3 m

A = π (radio²) = π (0.32 × 10^-3 m)² = 3.22 x 10^-7 m²

ℓ = 15 cm = 15 x 10^-2 m

R = ρ (ℓ/a) = 1.7 × 10^-8 Ω.m x (15 x 10^-2 m / 3.22 x 10^-7 m² ) = 7.9 × 10^-3 Ω = 7.9 m-Ohm.

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Sähköstaatiikka. Toimittanut Douglas Figueroa (USB).
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th. Ed Prentice Hall.
3. Resnick, r. (1999). Fyysinen. Osa. 2. 3^rata espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14^th. Ed. Nide 2.
5. Serway, R., Jewett, J. (2018). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. 10^mehu. Ed. Cengage -oppiminen.