Senoidiaaliset aaltoominaisuudet, osat, laskelmat, esimerkit

Se siniaalto Ne ovat aaltokuvioita, joita voidaan kuvata matemaattisesti sini- ja kosinifunktioilla. Ne kuvaavat perustellusti luonnollisia tapahtumia ja muuttuvia merkkejä ajassa, kuten sähkökasvien tuottamat jännitteet ja sitten niitä käytetään kodeissa, teollisuudessa ja kaduilla.

Sähköelementit, kuten vastus, kondensaattorit ja induktanssit, jotka yhdistyvät sinimuotoisiin jännitteen tuloihin, tuottavat myös vastauksia. Niiden kuvauksessa käytetty matematiikka on suhteellisen yksinkertaista, ja niitä on tutkittu perusteellisesti.

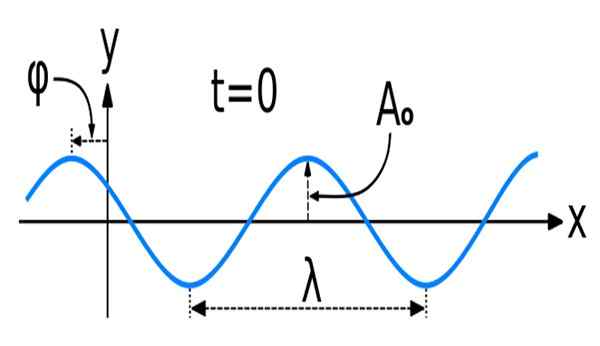
Kuvio 1. Siniaalto, jolla on joitain sen tärkeimmistä alueellisista ominaisuuksista: amplitudi, aallonpituus ja vaihe. Lähde: Wikimedia Commons. Wave_new_siine.SVG: KraaiNesTriginaalisesti luotu kosininaallona käyttäjän: Pelegs, kuten tiedosto: wave_new.SVGDERIVATIVE-työ: Dave3457 [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)]

Sinusoidisten tai sinimuotoisten aaltojen matematiikka, kuten ne myös tunnetaan, on sini- ja kosinitoiminnot.

Nämä ovat toistuvia funktioita, mikä tarkoittaa jaksollisuutta. Molemmilla on sama tapa, ja varaus, että kosiini on siirretty vasemmalle rinnan suhteen syklihuoneessa. Sitä havaitaan kuvassa 2:

Kuva 2. Sen X- ja COS X -funktiot siirtyvät toiseen suhteessa. Lähde: f. Zapata.

Sitten cos x = sin (x + π/2). Näiden toimintojen avulla siniaalto on edustettuna. Tätä varten kyseinen suuruus on asetettu pystysuuntaiselle akselille, kun taas vaakasuorassa akselissa aika sijaitsee.

Näiden toimintojen toistuvaa laatua arvostetaan myös yllä olevassa kaaviossa: kuvio toistetaan jatkuvasti ja säännöllisesti. Näiden toimintojen ansiosta voit ilmaista Sinian -tyypin jännitteet ja virrat ajan myötä asettamalla pystysuoraan akselille ja, eräs v tai yksi Yllyttää Edustaa jännitettä tai virtaa ja vaakasuora akselia x, Se t sää.

Yleisin tapa ilmaista siniaalto on:

v (t) = v_m synti (ωt+φ-A

Sitten syventämme tämän lausekkeen merkitystä määrittelemällä joitain perustermejä siniaalton karakterisoimiseksi.

[TOC]

Puolueet

Jakso, amplitudi, taajuus, sykli ja vaihe ovat käsitteitä sovelletaan jaksollisiin tai toistuviin aaltoihin, ja ne ovat tärkeitä karakterisoida ne oikein.

Ajanjakso

Määräajoallinen toiminto, kuten mainitut, joka toistetaan säännöllisin väliajoin, täyttää aina seuraavan kiinteistön:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) =… .

Missä T Se on määrä nimeltään Aalto, Ja on aika, joka tarvitaan saman vaiheen toistamiseen. Kansainvälisissä järjestelmäyksiköissä ajanjakso mitataan sekunnissa.

Amplitudi

Senoidisen aallon yleisen ilmaisun mukaan v (t) = v_m sin (ωt+φ), v_m Se on funktion maksimiarvo, joka tapahtuu sin (ωt+φ) = 1 (Muista, että suurin arvo, jonka sinus- ja kosini -funktio myöntää, on 1). Tämä maksimiarvo on juuri Aaltoamplitudi, tunnetaan myös huippuvamplitudi.

Jännitteen tapauksessa mitataan volteina ja jos se on virta, se on ampeereina. Siniaaltossa leveys on vakio, mutta muun tyyppisissä aaltoissa amplitudi voi vaihdella.

Voi palvella sinua: Resistanssilämpömittari: Ominaisuudet, toiminta, käyttö

Kiertää

Se on osa ajanjaksoa sisältävää aaltoa. Edellisessä luvussa ajanjakso vietiin mittaamalla se kahdesta peräkkäisestä piikistä tai harjanteista, mutta se voidaan alkaa mitata muusta aallon osasta, kun taas niitä rajoittaa ajanjakso.

Huomaa seuraavassa kuvassa yhtenä syklin kattajana pisteestä toiseen samalla arvolla (korkeus) ja sama kaltevuus (kallistus).

Kuva 3. Siniaaltossa sykli tapahtuu aina ajanjaksoksi. Tärkeää on, että lähtökohta ja loppu ovat samassa korkeudessa. Lähde: Boylestad. Johdanto piirianalyysiin. Pearson.

Taajuus

Syklien määrä esiintyy yhdessä sekunnissa ja liittyy sinusfunktion argumenttiin: ωt. Taajuus merkitään nimellä F Ja se mitataan sykliinä sekunnissa tai Hertz (HZ) kansainvälisessä järjestelmässä.

Taajuus on ajanjakson käänteinen määrä, siksi:

F = 1/t

Kun taas taajuus F liittyy Kulmataajuus ω (pulsaatio) kuten:

Ω = 2πF

Kulmataajuus ilmaistaan ​​radianeina /toiseksi kansainvälisessä järjestelmässä, mutta radiaanit ovat ulottumattomia, joten taajuus F ja kulmataajuus Ω Heillä on samat mitat. Huomaa, että tuote ωt antaa radiaanit seurauksena, ja se on otettava huomioon laskimella käytettäessä arvoa Sent.

Vaihe

Se vastaa aallon kokenut vaakasuuntaista siirtymistä suhteessa viitteenä otettuun aikaan.

Seuraavassa kuvassa vihreä aalto etenee suhteessa punaiseen aikaan t_{d -d}. Kaksi sinimuotoista aaltoa ovat vaihe Kun taajuus ja vaihe ovat samat. Jos vaihe eroaa, he ovat kuilu. Kuvio 2 aallot ovat myös vanhentuneita.

Kuva 4. Sinusidal -aaltoja. Lähde: Wikimedia Commons. Ei konetta luettavissa olevaa kirjailijaa. Kanjo ~ commonswikisi oletettu (perustuen tekijänoikeusvaatimuksiin). [Julkinen verkkotunnus].

Jos aaltojen taajuus on erilainen, ne ovat vaiheessa, kun vaihe ωt+φ olla sama molemmissa aaltoissa tietyinä hetkinä.

Senoidal Wave -generaattori

On monia tapoja saada sini -muotoinen signaali. Kotitekoiset juoksut tarjoavat heille.

Faradayn lain soveltaminen

Melko yksinkertainen tapa saada sinisignaali on käyttää Faradayn lakia. Tämä osoittaa, että suljetussa virranpiirissä, esimerkiksi magneettikentän keskellä asetettu silmukka, syntyy indusoitu virta, kun magneettikenttä virtaus sen läpi muuttuu ajan myötä. Näin ollen a Aiheuttama jännite jompikumpi fem.

Magneettikentän virtaus vaihtelee, jos silmukkaa pyöritetään vakiona kulman nopeudella kentän keskellä, joka on luotu kuvassa esitetyn magneetin napojen N ja S välissä.

Voi palvella sinua: Neptune (planeetta)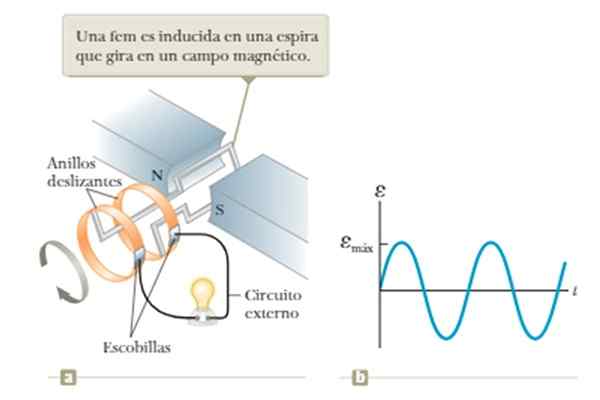Kuva 5. Aaltogeneraattori Faradayn induktiolakiin perustuva. Lähde: Lähde: Raymond A. Serway, Jonh W. Jewett [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)].

Tämän operaattorin rajoitus on riippuvuus jännitteestä, joka saadaan silmukan kiertotaajuudella, kuten esimerkiksi esimerkissä 1 nähdään yksityiskohtaisemmin.

Wien -oskillaattori

Toinen tapa saada siniaalto, tällä kertaa elektronilla. Tällä tavoin saadaan siniaaltoja, joiden taajuus ja amplitudi käyttäjä voi muokata mukavuuden mukaan kytkimen säätämisen avulla.

Kuvio näyttää siniagnaaligeneraattorin, jolla voidaan saada myös muita aaltomuotoja: kolmionmuotoiset ja neliöt muun muassa.

Kuva 6. Signaaligeneraattori. Lähde: Lähde: Wikimedia Commons. Opggge englanniksi Wikipedia [CC BY-SA 3.0 (https: // creativecommons.Org/lisenssit/by-SA/3.0)].

Kuinka laskea siniaaltoja?

Laskelmien suorittamiseksi, joihin sisältyy siniaaltoja, käytetään tieteellistä laskin. Näillä laskimilla on tiloja, jotka toimivat kulmien toimintaan joko asteina tai radianeina, ja on helppo muuntaa yksi tapa toiseen. Muutoskerroin on:

180 º = π Radianit.

Laskinmallin mukaan sinun on liikkuttava moodiavaimen kautta löytääksesi tutkinto -vaihtoehdon, jonka avulla voit työskennellä trigonometristen toimintojen parissa asteina tai RAD -vaihtoehdolla, jotta voit suoraan työskennellä radianien kulmissa.

Esimerkiksi sin 25 º = 0.4226 Laskurin ollessa asetettu DEG -tilassa. Muunnat 25 º radianiksi, saat 0.4363 Radianes ja SEN 0.4363 rad = 0.425889 ≈ 0.4226.

Oskilloskooppi

Oskilloskooppi on laite, joka mahdollistaa visualisoinnin jännitteiden ja virtausten näytön merkkeissä sekä vaihtoehtoisia että suoria. Siinä on nuppeja signaalin koon säätämiseksi ruudukossa seuraavassa kuvassa:

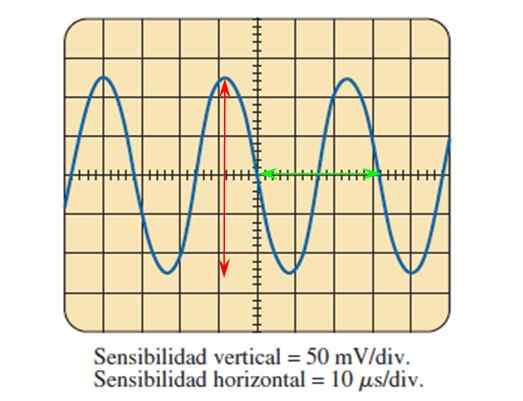Kuva 7. Sinusoidinen signaali mitattu oskilloskoopilla. Lähde: Boylestad.

Oskilloskoopin tarjoaman kuvan kautta ja herkkyyden säätämisen molemmissa akseleissa on mahdollista laskea yllä kuvattuja aaltoparametreja.

Voi palvella sinua: elliptiset galaksit: muodostuminen, ominaisuudet, tyypit, esimerkit

Kuvio näyttää siniajännitesignaalin ajan funktiona, jossa jokainen pystysuoran akselin jakautuminen on 50 millivoltin arvoinen, kun taas vaaka -akselilla jokainen jako on 10 mikrosekuntia arvoinen.

Piikin huippuamplitudi laskee aallon kattamat divisioonat pystysuunnassa auttaen punaisella nuolella:

5 divisioonaa lasketaan punaisen nuolen avulla, joten piikkijännite on:

V_pp = 5 divisioonaa x 50 mV/jako = 250 mV.

Pico -jännite V_p Se mitataan vaaka -akselista, koska se on 125 mV.

Kauden löytämiseksi sykli mitataan, esimerkiksi vihreän nuolen rajattu, joka kattaa 3.2 divisioonaa, sitten ajanjakso on:

T = 3.2 jakoa x 10 mikrosekuntia/jako = 32 mikrosekuntia = 32 μs

Esimerkit

Esimerkki 1

Kuvan 3 generaattorille osoita Faradayn laista, että indusoidulla jännitteellä on sinia. Oletetaan, että silmukka koostuu N -käännöksistä yhden sijasta, kaikilla samalla alueella A ja kääntyy jatkuvalla kulma -nopeudella ω magneettikentän keskellä B - yhtenäinen.

Ratkaisu

Faradayn laissa sanotaan, että indusoitu fem ε On:

ε = -n (dφ_{B -} /dt)

Missä Φ_{B -} Se on muuttuva magneettikentän virtaus, koska se riippuu siitä, kuinka silmukka altistuu kentälle joka hetki. Negatiivinen merkki kuvaa yksinkertaisesti sitä tosiasiaa, että tämä fem vastustaa sitä tuottavaa syytä (Lenzin laki). Yhdestä silmukasta johtuva virtaus on:

Φ_{B -} = B.-Lla.cos θ

θ on kulma, jonka normaali vektori silmukan tasoon muodostuu kentällä B - Kun kierto tapahtuu (katso kuva), tämä kulma vaihtelee luonnollisesti seuraavasti:

θ = ωt

Jotta: Φ_{B -} = B.-Lla.cos θ = b.-Lla.koos ωt. Nyt sinun on vain johdettava tämä lauseke ajan suhteen, ja sen kanssa saadaan fem: lle:

ε = -n.d (b.-Lla.koos ωt) /dt

Kuin kenttä B - Se on tasainen ja spaasi -alue ei vaihtele, ne jättävät johdannaisen:

ε = -nba. D (cos ωt) /dt = ωnba. Senttiä ωt

Esimerkki 2

Silmukan pinta -ala on 0.100 m² ja käänny 60: een.0 Rev/s, sen kierto -akselin kohtisuorassa tasaiseen magneettikenttään 0.200 t. Tietäen, että kela on 1000 käännöstä löytää: a) generoidun maksimaalisen fem, b) kelan suunta suhteessa magneettikenttään, kun maksimaalinen indusoitu FEM tapahtuu.

Kuva 8. N -kierroksen spiraali, joka on rikki tasaisen magneettikentän keskellä ja tuottaa sinisignaalin. Lähde: r. Serway, fysiikka luonnontieteiden ja tekniikan fysiikka. Nide 2. Cengage -oppiminen.

Ratkaisu

a) Suurin fem on ε_Max = Ωnba

Ennen arvojen korvaamista, 60 kierrosluvun taajuus kansainvälisen järjestelmän yksiköille on läpäistävä. On tiedossa, että yksi vallankumous vastaa käännöstä tai 2p -radianeja:

60 60.0 Rev/S = 120p radianit/s

ε_Max = 120p radianit x 1000 kierrosta x 0.200 t x 0.100 m² = 7539.82 V = 7.5 kV

b) Kun tämä arvo tapahtuu Senttiä ωt = 1 siksi:

ωt = θ = 90º,

Tässä tapauksessa spiraalitaso on yhdensuuntainen B -, niin että normaali vektori mainitulle tasolle muodostaa 90º kentän kanssa. Tämä tapahtuu, kun kuvion 8 musta vektori on kohtisuorassa vihreää vektoria kohtaan, joka edustaa magneettikenttää.

Viitteet

1. Boylestad, r. 2011. Johdanto piirianalyysiin. 12. päivä. Painos. Pearson. 327-376.
2. Figueroa, D. 2005. Sähkömagnetismi. Fyysinen sarja tiedettä ja tekniikkaa. Osa 6. Toimittanut D. Figueroa. Simon Bolivarin yliopisto. 115 ja 244-245.
3. Figueroa, D. 2006. Fysiikan laboratorio 2. Toimituksellinen päiväntasaus. 03-1 ja 14-1.
4. Siniaalto. Toipunut: iessierradgara.com
5. Serway, R. 2008.Fysiikka tieteen ja tekniikan fysiikka. Nide 2. Cengage -oppiminen. 881-884