Kiinteät aaltojen kaavat, ominaisuudet, tyypit, esimerkit

Se seisovat aallot Ne ovat aaltoja, jotka leviävät rajoitetulle puoliskolle, menevät ja tulevat osaan tilaa, toisin kuin matkustavat aallot, jotka etenevät heistä, jotka etenevät heistä ja eivät palaa siihen.

Ne ovat soittimissa tuotetun äänen perusta. Ne luodaan myös kireisiin kalvoihin, kuten rummut tai putkien sisä- ja rakenteet, kuten sillat ja rakennukset.

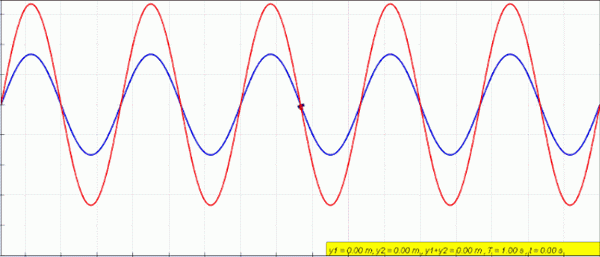Animaatio paikallaan olevasta (punaisesta) aallosta, joka on luotu vasemman (sinisen) ja oikean aallon (vihreä) superpositiolla (vihreä). Lähde: Lootangmany Kiitos alkuperäisen simulaation kirjoittajalle = Wolfgang Christian ja Francisco Schembre -kirjailija Easy Java Simulation = Francisco Schembre/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/4.0)

Kun molemmissa päissä on kiinteä köysi, kuten esimerkiksi kitara, aallot luodaan identtisellä amplitudilla ja taajuudella, jotka kulkevat vastakkaisissa aisteissa ja yhdistävät nimeltään ilmiön puuttuminen.

Jos aallot ovat vaiheessa, harjanteet ja laaksot ovat kohdistettuja ja johtavat aaltoon kaksois amplitudilla. Siinä tapauksessa puhutaan rakentavasta häiriöstä.

Mutta jos häiritsevät aallot ovat vaiheen ulkopuolella, yhden harjanteet kohtaavat muiden laaksot ja tulosten amplitudi on nolla. Se on sitten tuhoisa häiriö.

[TOC]

Kaavat ja yhtälöt

Aallon pääelementit, jotka edustavat sitä tilassa ja ajassa, ovat sen amplitudi A, sen aallonpituus λ ja sen kulmataajuus ω.

Aallon elementit. Lähde: Wikimedia Commons.

Matemaattisessa esityksessä on suositeltavaa käyttää k: tä kuin Aaltoluku o Kuinka monta kertaa aalto yksikköä kohti tapahtuu. Siksi se määritetään λ -aallon pituuden kautta, joka on kahden laakson tai kahden harjanteen välinen etäisyys:

K = 2π/ λ

Samalla kun kulmataajuus Se liittyy täydellisen värähtelyn ajanjaksoon tai kestoon, kuten:

Ω = 2π/ t

Ja myös taajuus F on annettu:

F = ω / 2π

Siksi:

F = 1/t

Lisäksi aallot liikkuvat nopeudella v mukaan:

v = λ.F

Paikallaan olevan aallon matemaattinen ilmaisu

Matemaattisesti voimme ilmaista aallon sinusfunktion tai kosinifunktion kautta. Oletetaan

ja₁ = Synti (kx - ωt)

ja₂ = Synti (kx + ωt)

Niitä lisäämällä löydämme tuloksena olevan aallon ja_{R -}-

ja_{R -} = y₁ + ja₂ = SEN (kx - ωt) + synti (kx + ωt)

Summan löytämiseksi on trigonometrinen identiteetti:

Voi palvella sinua: mikä on suhteellinen ja ehdoton karheus?

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Tämän identiteetin kautta tuloksena oleva aalto ja_{R -} on jäljellä:

ja_{R -} = [2A Sen KX] . cos ωt

Solmujen ja vatsan sijainti

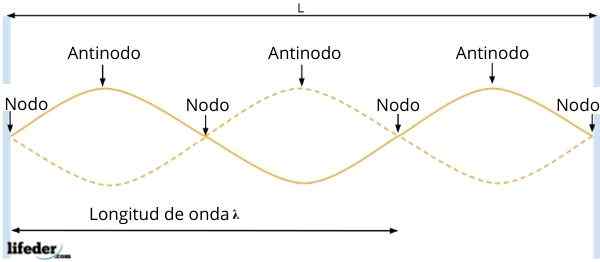Antinodot tai vatsat ja solmut

Tuloksena olevalla aaltolla on amplitudi_{R -} = 2Ase KX, joka riippuu hiukkasen sijainnista. Sitten niiden pisteissä, joissa Sen KX = 0, aallon amplitudi peruutetaan, ts. Värähtelyä ei ole.

Nämä kohdat ovat:

Kx = π, 2π, 3π ..

Kuten k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

Tällaisissa kohdissa tapahtuu tuhoisia häiriöitä, ja niitä kutsutaan solmut. Ne erotetaan etäisyydellä, joka on yhtä suuri kuin λ/2, kuten edellisestä tuloksesta johdetaan.

Ja kahden peräkkäisen solmun välillä ovat antinodot tai vatsa, jossa aallon amplitudi on suurin, koska rakentava häiriö tapahtuu. Ne tapahtuvat, kun:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Jälleen k = 2 π/ λ ja sitten: sitten:

x = λ /4, 3λ /4, 5λ /4, ..

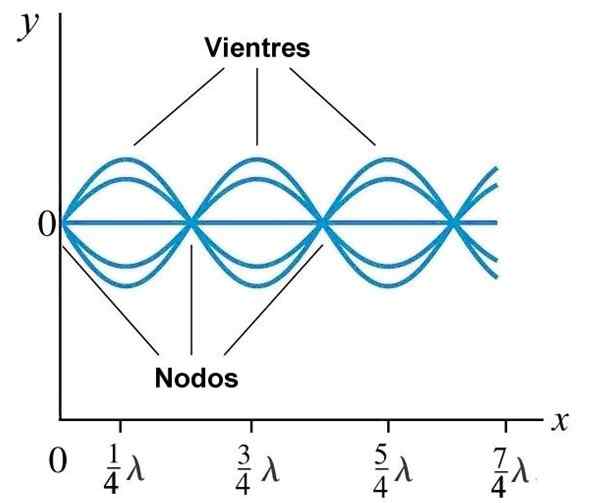Vatsa tai antinodit ja solmut paikallaan olevassa aallossa, joka on muodostettu köydellä, jonka pääty on x = 0. Lähde: Wikimedia Commons.

Normaalit moodit köydellä

Köyden rajaolosuhteet määrittävät, kuinka aallonpituudet ja taajuudet ovat. Jos köyden pituus L kiinnitetään sen kahdella päällä, se ei voi värähtelyä millään taajuudella, koska pisteet, joissa köysi kiinnitetään, ovat jo solmuja.

Lisäksi vierekkäisten solmujen välinen erotus on λ/2, ja solmun ja vatsan välillä se on λ/4, tällä tavalla vain tietyille aallonpituuksille tuotetaan paikallaan olevia aaltoja: niitä The:

(λ/2) = l, n = 1, 2, 3, 4 .. .

Siksi:

λ = 2L/N

Harmoniset

Erilaisia ​​arvoja λ kutsutaan harmoniset. Siten meillä on:

-Ensimmäinen harmoninen: λ = 2L

-Toinen harmoninen: λ = l

-Kolmas harmoninen: λ = 2 l/3

-Harmoninen huone: λ = l/2

Ja niin edelleen.

Nopeus ja taajuus

Vaikka paikallaan oleva aalto ei näytä liikkuvan, yhtälö on edelleen voimassa:

v = λ. F

Siksi:

V = (2L/N) . F

F = nv/2l

Nyt voidaan osoittaa, että nopeus, jolla aalto liikkuu köydessä, riippuu samassa T -jännitteestä ja sen lineaarisesta tiheydestä μ (massa pituusyksikköä kohti) kuten:

Siksi:

Voi palvella sinua: Kuolleet kuormat: Ominaisuudet, laskelmat, esimerkit

Paikallaan olevien aaltojen ominaisuudet

-Kun aallot ovat paikallaan, tuloksena oleva aalto ei leviä sen komponenttien tavoin, jotka menevät paikasta toiseen. On pisteitä, joissa y = 0, koska tärinää ei ole: solmut, toisin sanoen amplitudi_{R -} Se on nolla.

-Kiinteän aallon matemaattinen ilmaisu koostuu alueellisen osan tuotteesta (joka riippuu X -koordinaatista tai avaruuskoordinaateista) ja ajallisesta osasta.

-Solmujen joukossa tuloksena oleva musta aalto värähtelee yhdessä paikassa, kun taas paikasta toiseen kulkevat aallot ovat vanhentuneita.

-Vain solmuissa energiaa ei kuljeteta, koska tämä on verrannollinen amplitudin neliöön, mutta se on loukussa solmujen välillä.

-Vierekkäisten solmujen välinen etäisyys on puolet aallonpituudesta.

-Pisteitä, joissa köysi on kiinnitetty, pidetään myös solmuina.

Kaverit

Paikallaan olevat aallot ulottuvuudessa

Kiinteän köyden aallot ovat esimerkkejä kiinteistä aaltoista ulottuvuudessa, jonka matemaattinen kuvaus tarjoamme edellisissä osissa.

Paikallaan olevat aallot kahdessa ja kolmessa ulottuvuudessa

Kiinteät aallot voidaan esitellä myös kahdessa ja kolmessa ulottuvuudessa, mikä on hieman monimutkaisempi matemaattinen kuvaus.

Kilpailu ondas -esimerkkejä

Kiinteät jouset

-Extreme -korjattu merkkijono, joka on heilahtettu käsin tai yhden männän kanssa toisella, tuottaa paikallaan olevia aaltoja sen pituudella.

Soittimet

Kiinteät aallot luodaan soittimiin, kuten Violoncello. Lähde: Pixabay.

-Kun soitat jousisoittimia, kuten kitara, harppu, viulu ja piano.

STLOVER -aallot luodaan myös ilmaputkiin, kuten elinputket.

Rakennukset ja sillat

Kiinteät aallot syntyvät rakenteissa, kuten sillat ja rakennukset. Huomattava tapaus oli Tacoma Narrows -jousitussilta lähellä Seattlen kaupunkia, Yhdysvallat. Pian sen jälkeen, kun se oli aloitettu vuonna 1940, tämä silta romahti tuulen sisälle luotujen paikallaan olevien aaltojen takia.

Tuulen taajuus sopii sillan luonnolliseen taajuuteen, mikä aiheutti tässä paikallaan olevia aaltoja, jotka kasvattivat niiden amplitudia, kunnes silta romahti. Ilmiö tunnetaan nimellä resonanssi.

Se voi palvella sinua: kevyt heijastus

Seitsy

Satamissa on erittäin utelias ilmiö, nimeltään Seitsy, jossa meren aallot tuottavat suuria värähtelyjä. Tämä johtuu siitä, että sataman vedet ovat melko suljettuja, vaikka valtameren vedet tunkeutuvat niin usein sataman sisäänkäynnin läpi.

Satamavesi liikkuvat omalla taajuudellaan, samoin kuin valtameren vesi. Jos molemmat vedet vastaavat taajuuksiaan, resonanssin vuoksi on suuri paikallaan oleva aalto, kuten Tacoma -sillan kanssa tapahtui.

Se Seitsy Niitä voi esiintyä myös järvissä, säiliöissä, uima -altaissa ja muissa vesirunkoissa, jotka rajoittavat pinnat.

Kalasäiliöt

Kiinteät aallot voidaan luoda henkilön kuljettamassa kalakappaleessa, jos taajuus, jolla henkilö on yhtä suuri kuin veden kääntymisen taajuus.

Liikuntaa

Kitaraköysi on L = 0.9 m ja lineaarinen taikinatiheys μ = 0.005 kg/m. Sille altistetaan 72 N jännitettä ja sen tärinätila on se, joka näyttää kuvan, amplitudi 2a = 0.5 cm.

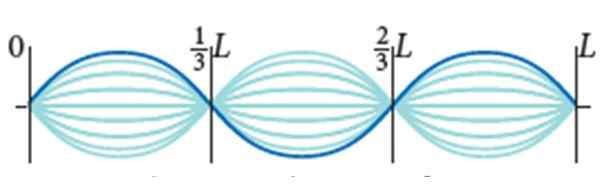Kiinteät aallot kitaraköydellä. Lähde: Bauer, W. Fyysinen.

Löytö:

a) etenemisnopeus

b) aaltotaajuus

c) vastaava kiinteä aaltoyhtälö.

Liittää jhk

Kautta:

Saadaan;

V = [72 N/(0.005 kg/m)]^1/2  = 120 m/s.

Ratkaisu b

Kahden vierekkäisen solmun välinen etäisyys on λ/2, siksi:

(2/3) l - (1/3) l = λ/2

(1/3) l = λ/2

λ = 2L/3 = 2 x 0.90 m / 3 = 0.60 m.

Kuten v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Liuos C

Yhtälö on:

ja_{R -} = [2A Sen KX] . cos ωt

Meidän on korvattava arvot:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π HZ.

2A -amplitudi annetaan jo lausunnolla:

2a = 0.5 cm = 5 x 10 ^-3 m.

Siksi:

ja_{R -} = 5 x 10 ^-3 m . synti [(10π/3) x] . cos (400πt) =

= 0.5 cm . synti [(10π/3) x] . cos (400πt)

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.
2. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 7. Aallot ja kvanttifysiikka. Toimittanut Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
5. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti.
6. Wikipedia. Seitsy. Palautettu: on.Wikipedia.org.