Yksidimensionaaliset aallot matemaattiset ilmaisut ja esimerkit

Se Yksidimensionaaliset aallot Ne leviävät yhteen suuntaan riippumatta siitä, tapahtuuko tärinä vai ei samassa etenemissuunnassa. Hyvä esimerkki heistä on aalto, joka liikkuu kitaran kaltaista kireää köyttä pitkin.

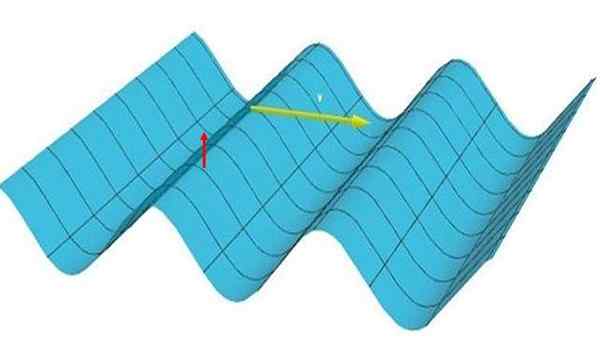
Tasaisella aaltolla ylittää, Hiukkaset värähtelevät pystysuunnassa (ne kiipeävät ja menevät alas, katso punainen nuoli kuvassa 1), mutta se on yksi -ulottuvuus, koska häiriö kulkee yhteen suuntaan, keltaisen nuolen seurauksena.

Kuva 1: Kuva edustaa yhden dimensionaalista aaltoa. Huomaa, että harjanteet ja laaksot muodostavat yhdensuuntaiset viivat toistensa kanssa ja kohtisuorassa etenemissuuntaan nähden. Lähde: Itse tehty.

Yksidimensionaaliset aallot ilmestyvät melko usein jokapäiväisessä elämässä. Seuraavassa osassa kuvataan joitain esimerkkejä niistä ja myös aaltoista, jotka eivät ole yksidimensioisia, erot selkeästi.

[TOC]

Esimerkkejä yksidimensioisista aaltoista ja ei -ulottumattomista aaltoista

Yksidimensionaaliset aallot

Nämä ovat joitain esimerkkejä yhdestä ulottuvuudesta aaltoista, joita voidaan helposti havaita:

- Äänipulssi, joka kulkee suoran palkin läpi, koska se on häiriö, joka leviää baariin.

- Aalto, joka kulkee vesikanavan läpi, vaikka veden pinnan siirtyminen ei ole yhdensuuntainen kanavan kanssa.

- Aallot, jotka leviävät pinnalle tai kolmen ulottuvuuden tilaa, voivat myös olla yksi dimensioinen, edellyttäen, että niiden aaltoalueet ovat tasot, jotka ovat yhdensuuntaisia ​​ja kulkevat yhteen suuntaan.

Ei -ulottuvuusaallot

Esimerkki ei -ulottumattomasta aaltosta löytyy aaltoista, jotka muodostetaan vielä veden pinnalle, kun kivi pudotetaan. Se on lieriömäisen aallon kaksiulotteinen aalto -etuosa.

Voi palvella sinua: Lever ArmKuva 2. Kuva edustaa esimerkkiä siitä, mikä ei ole yhden ulottuvuuden aalto. Huomaa, että harjanteet ja laaksot muodostavat ympyröitä ja etenemissuunta on säteittäinen ulospäin, se on sitten kahden dimensioinen pyöreä aalto. Lähde: Pixabay.

Toinen esimerkki unionin ei-ulottuvuudesta on ääniaalto, joka tuottaa sähinkäisen räjähdyksen tietyllä korkeudella. Tämä on kolmiulotteinen aalto pallomaisella aaltoalueella.

Yhden ulottuvuuden aallon matemaattinen ilmaisu

Yleisin tapa ilmaista yhden dimensionaalinen aalto, joka leviää ilman vaimenemista akselin positiiviseen suuntaan x Ja nopeudella v Se on matemaattisesti:

ja (x, t) = f (x - v.t)

Tässä ilmaisussa ja edustaa aseman häiriötä x Heti t. Aaltomuoto antaa funktiolla F. Esimerkiksi kuvassa 1 esitetty aaltofunktio on:  ja (x, t) = cos (x - v t) ja aallon kuva vastaa hetkeä t = 0.

Tällaista aaltoa, jota kuvataan kosini- tai sinusfunktiolla, kutsutaan harmoninen aalto. Vaikka se ei ole ainoa olemassaolo, se on erittäin tärkeä, koska mikä tahansa muu aalto voidaan edustaa päällekkäisyytenä tai harmonisten aaltojen summana. Se on tuttava Fourier -lause, niin käytetään kuvaamaan kaikenlaisia ​​signaaleja.

Kun aalto kulkee X -akselin negatiiviseen suuntaan, se vain muuttuu v ohella -v Väitteenä, oleminen:

ja (x, t) = g (x + v t)

Kuvio 3 näyttää vasemmalle kulkevan aallon animaation: se on muoto, jota kutsutaan funktioksi Lorentziana ja hän Matemaattinen ilmaisu on:

Voi palvella sinua: työ: kaava, yksiköt, esimerkit, harjoitukset

ja (x, t) = 1 / (1 + (x + 1⋅t)²

Tässä esimerkissä etenemisen nopeus on V = 1, -jokaiselle aikayksikölle-.

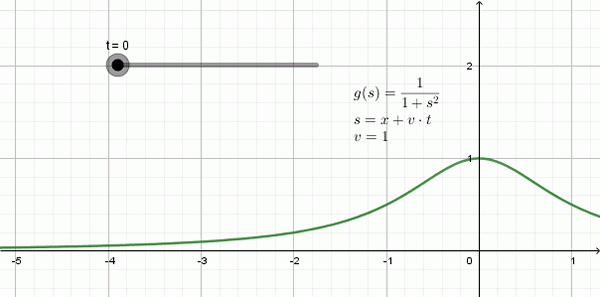Kuva 3. Esimerkki Lorentzian aalto, joka kulkee vasemmalle nopeasti V = 1. Lähde: valmistettu f. Zapata geogebralla.

Yksidimensionaalinen aaltoyhtälö

Aaltoyhtälö on yhtälö osittaisissa johdannaisissa, joiden ratkaisu on tietysti aalto. Se luo matemaattisen suhteen alueellisen osan ja sen ajallisen osan välillä, ja sillä on muoto:

Ratkaisu, joka on juuri funktio y (x, t), voidaan varmistaa korvaamalla ja kehittämällä tässä yhtälössä. Esimerkiksi toiminnot f (x - v t)  ja  G (x + VT)  mainittu, ne ovat aaltoyhtälöratkaisuja.

Ratkaistu esimerkki

Sitten sinulla on yleinen lauseke y (x, t) harmoniselle aaltolle:

ja (x, t) = a⋅cos (k⋅x ± ω⋅t + θo)

a) Kuvaile parametrien fyysistä merkitystä A, K, ω ja θo.

b) Millä merkityksellä on merkit ± kosenon väitteessä?

c) Varmista, että annettu lauseke on todellakin edellisen osan aaltoyhtälön ratkaisu ja etsi nopeus v eteneminen.

Ratkaisu)

Aallon ominaisuudet ovat seuraavissa parametreissa:

--Lla edustaa amplitudi tai "aallonkorkeus".

-K on Aaltoluku Ja se liittyy aallonpituuteen λ kautta K = 2π/ λ.

-Ω Se on fkulman laajeneminen Ja se liittyy ajanjakso T aallon heilahtelu

Ω = 2π/ t.

-θo Se on alkuvaihe, joka liittyy aallon lähtökohtaan.

Voi palvella sinua: Staattinen kitka: Kerroin, esimerkki, liikunta

Ratkaisu b)

Negatiivinen merkki otetaan, jos aalto kulkee X -akselin positiiviseen suuntaan ja positiivinen merkki muuten.

Liuos c)

Varmista, että annettu lauseke on ratkaisu aaltoyhtälöön on yksinkertainen: funktion osittainen johdannainen otetaan ja (x, t) Kahdesti X: n suhteen se on osittain johdettu T: stä kahdesti ja sitten molemmat tulokset kohtaavat tasa -arvon saamiseksi:

Toinen johdettu x: ∂²ja/ ∂x²= -K². -Lla⋅cos (k⋅x ± ω⋅t + θo)

Toinen johdettu t: ∂²ja/ ∂t²= -Ω². -Lla⋅cos (k⋅x ± ω⋅t + θo)

Nämä tulokset korvataan aaltoyhtälössä:

 -k -k -². -Lla⋅cos (k⋅x ± ω⋅t + θo) = (1/V²) (-Ω². -Lla⋅cos (k⋅x ± ω⋅t + θo))

Niin paljon -Lla Koska kosini yksinkertaistetaan, koska ne ilmestyvät tasa -arvon molemmille puolille ja kosinin argumentti on sama, siksi lauseke pelkistetään:

-k -k -² = (1/V²) (-Ω²-A

Se mahdollistaa yhtälön saamisen v suhteen Ω ja k -k --

v² = Ω² / k²

v = ± Ω / k

Viitteet

1. Sähköinen koulutus. Yksidimensionaalisten harmonisten aaltojen yhtälö. Toipunut: e-ducative.Katedu.On
2. Fysiikan rincón. Aaltoluokat. Haettu: fysiikka.Blogin.com.
3. Figueroa, D. 2006. Aallot ja kvanttifysiikka. Sarja: Tieteen ja tekniikan fysiikka. Toimittanut Douglas Figueroa. Simon Bolivarin yliopisto. Caracas Venezuela.
4. Fysiikan laboratorio. Aaltoliike. Toipunut: fisikab.com.
5. Peirce, a. Luento 21: Yhden ulottuvuuden aaltoyhtälö: D'Alembertin ratkaisu. Haettu osoitteesta: UBC.Ac.
6. Aaltoyhtälö. Haettu: vuonna.Wikipedia.com