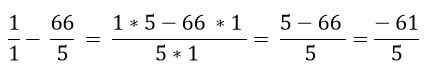Papruda

Mikä on papruda?

Hän Papruda Se on menettely algebrallisten lausekkeiden ratkaisemiseksi. Sen lyhenne osoittaa operaatioiden prioriteettijärjestyksen: Suluet, valtuudet, kertolasku, jako, lisäys ja vähennys. Tätä sanaa käyttämällä voit helposti muistaa järjestyksen, jossa useista toiminnoista koostuva lauseke on ratkaistava.

Yleensä numeerisissa lausekkeissa löydät useita aritmeettisia operaatioita yhdessä, kuten summat, vähennys, kertolaskut ja jakautumiset, jotka voivat olla myös fraktioita, voimia ja juuria. Niiden ratkaisemiseksi on tarpeen noudattaa menettelyä, joka takaa tulosten oikeat.

Näiden operaatioiden yhdistelmästä koostuva aritmeettinen lauseke on ratkaistava järjestyksen prioriteetin mukaisesti, joka tunnetaan myös nimellä operaatioiden hierarkia, joka on perustettu kauan sitten yleisissä yleissopimuksissa. Siksi kaikki ihmiset voivat noudattaa samaa menettelyä ja saada saman tuloksen.

Ominaisuudet

Papomudat on vakiomenettely, joka vahvistaa järjestyksen, jota on noudatettava, kun on annettava lauseke, joka koostuu operaatioiden yhdistelmästä, kuten vähennyssumma, kertolasku ja jako.

Tämä menettely vahvistaa operaation prioriteettijärjestyksen suhteessa muihin heidän tuolloin; eli jokaisella operaatiolla on hierarkkinen muutos tai ratkaiseva taso.

Järjestys, jossa lausekkeen eri toiminnot on ratkaistava. Tällä tavalla sinun on:

1. PA: Suluet, neliömäiset kiinnikkeet tai avaimet.
2. PO: voimat ja juuret.
3. MU: LIIKETOIMINTA.
4. D: Divisions.
5. V: Lisäykset tai summat.
6. S: Vähennys tai vähennys.

Tätä menettelyä kutsutaan myös englanniksi pemdasiksi; Tämän sanan helposti muistaminen liittyy lauseeseen: "Anteeksi rakas tätini Sally”, Missä kukin alkukirjaus vastaa aritmeettista operaatiota, samalla tavalla kuin papomudat.

Kuinka ratkaista ne?

Papomudasin perustaman hierarkian perusteella lausekkeen toiminnan ratkaisemiseksi on välttämätöntä täyttää seuraava järjestys:

• Ensinnäkin kaikki ryhmittelysymbolien, kuten sulujen, avaimet, sulukot ja murto -palkit, on ratkaistava operaatiot. Kun muissa on ryhmittelysymboleja, sinun pitäisi alkaa laskea sisältä.

Voi palvella sinua: neliömäiset peräkkäit: Esimerkkejä, sääntöä ja harjoituksia ratkaistu

Näitä symboleja käytetään muuttamaan järjestystä, jossa toiminnot on ratkaistu, koska se, mikä on aina näiden sisällä, on aina ratkaistava.

• Sitten voimat ja juuret ratkaistaan.
• Kolmanneksi kertoimet ja divisioonat ratkaistaan. Näillä on sama prioriteettijärjestys; Siksi, kun nämä kaksi toimintaa löytyy lausekkeesta, se, joka näyttää ensin, on ratkaistava, lukemalla lauseke vasemmalta oikealle.
• Viime kädessä summat ja vähennystä ratkaistaan, joilla on myös sama prioriteettijärjestys, ja siksi se on ratkaistu, joka ilmestyy ensin lausekkeessa, luettu vasemmalta oikealle.
• Operaatioita ei tule koskaan sekoittaa, kun luet vasemmalta oikealle, sinun on aina noudatettava Papomudasin perustaman prioriteetti- tai hierarkian järjestystä.

On tärkeää muistaa, että kunkin operaation tulos on asetettava samaan järjestykseen suhteessa muihin, ja kaikki välivaiheet on erotettava merkistä, kunnes lopputulos saavutetaan, kunnes saavutetaan lopputulos.

Soveltaminen

Papomudas -menettelyä käytetään, kun sinulla on yhdistelmä erilaisia ​​operaatioita. Ottaen huomioon, kuinka ne ratkaistaan, sitä voidaan soveltaa:

Lausekkeet, jotka sisältävät summia ja vähennystä

Se on yksi yksinkertaisimmista toimista, koska molemmilla on sama prioriteettijärjestys, joten se on ratkaistava ilmaisun vasemmalta oikealle; Esimerkiksi:

22 -15 + 8 +6 = 21.

Lausekkeet, jotka sisältävät summia, vähennystä ja kertolaskua

Tässä tapauksessa ensisijainen toiminta on kertolasku, silloin summat ja vähennystä ratkaistaan ​​(se, joka on ensimmäinen lausekkeessa). Esimerkiksi:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Lausekkeet, jotka sisältävät summan, vähennyskertoimen ja jaon

Tässä tapauksessa on yhdistelmä kaikkia operaatioita. Se alkaa ratkaisemalla kertolasku ja jako, jolla on ylivoimainen prioriteetti, sitten summat ja vähentäminen. Lukemalla lauseketta vasemmalta oikealle, se ratkaistaan ​​sen hierarkian ja aseman mukaan; Esimerkiksi:

Voi palvella sinua: Mumm

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Lausekkeet, jotka sisältävät summan, vähentämisen, kertolaskun, jakautumisen ja valtuudet

Tässä tapauksessa yksi numeroista on nostettu voimaan, joka prioriteettitason sisällä on ensin ratkaistava ja ratkaista sitten kertolaskut ja divisioonat ja lopulta summat ja vähennys:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Kuten valtuudet, juurilla on myös toinen prioriteettijärjestys; Siksi niitä sisältävissä lausekkeissa ne on ensin ratkaistava kuin kertolaskut, divisioonat, summat ja vähentäminen:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Lausekkeet, jotka käyttävät ryhmittelysymboleja

Kun käytetään merkkejä, kuten suluista, avaimista, suluista ja fraktiopalkista, jotka ovat näiden sisällä ratkaistaan ​​ensin riippumatta sen sisältävien operaatioiden prioriteettijärjestyksestä suhteessa tämän ulkopuolella oleviin, ikään kuin se käsittelee erillistä ilmaisu:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Jos tässä on useita operaatioita, ne on ratkaistava hierarkkisella järjestyksellä. Sitten muut lausekkeen muodostavat toiminnot ratkaistaan; Esimerkiksi:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

Joissakin lausekkeissa käytetään toisten symbolien ryhmittelyä, kuten silloin, kun on tarpeen muuttaa operaation merkki. Näissä tapauksissa sen on aloitettava ratkaisemalla sisäpuolelta; toisin sanoen yksinkertaistaminen lausekkeen keskellä olevien ryhmittelysymbolien yksinkertaistaminen.

Yleensä näiden symbolien sisältämien toimintojen ratkaisemismääräys on: ratkaise ensin se, mikä on suluissa (), sitten suluissa [] ja lopuksi avaimet .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Voi palvella sinua: teoreettinen todennäköisyys: Kuinka saada se ulos, esimerkkejä, harjoituksia

= 90 - 3 _* 24

= 90 - 72

= 18.

Harjoitukset

Ensimmäinen harjoitus

Etsi seuraavan lausekkeen arvo:

kaksikymmentä² + √225 - 155 + 130.

Ratkaisu

Papomudien soveltaminen, valtuudet ja juuret on ratkaistava ensin, ja sitten lisää ja vähennä. Tässä tapauksessa kaksi ensimmäistä operaatiota kuuluvat samaan järjestykseen, joten ensimmäinen ratkaistaan ​​vasemmalta oikealle:

kaksikymmentä² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Lisää sitten ja vähennä, aloittaen myös vasemmalla:

400 + 15 -155 + 130

= 390.

Toinen harjoitus

Etsi seuraavan lausekkeen arvo:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Ratkaisu

Se alkaa ratkaisemalla suluissa olevat operaatiot noudattaen hierarkkista järjestystä, jota heillä on Papomudan mukaan.

Ensin ensimmäisen sulujen valtuudet on ratkaistu, sitten toisen sulkujen toiminnot on ratkaistu. Koska ne kuuluvat samaan järjestykseen, lausekkeen ensimmäinen toiminta on ratkaistu:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216- 729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Koska suluissa olevat operaatiot on jo ratkaistu, nyt jatkoa, jolla on suurin hierarkia, jatketaan:

[- (-513) ÷ (3)] = [- (-171)]]]].

Lopuksi, sulku, joka erottaa miinus (-) -merkin tuloksesta, joka tässä tapauksessa on negatiivinen, osoittaa, että näiden merkintöjen kertominen on tehtävä. Siten lausekkeen tulos on:

[- (-171)] = 171.

Kolmas harjoitus

Etsi seuraavan lausekkeen arvo:

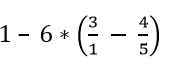
Ratkaisu

Suluissa olevat fraktiot on ratkaistu:

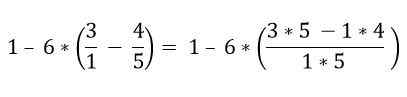
Suluissa on useita operaatioita. Kerrointiedot ratkaistaan ​​ensin ja sitten vähennykset; Tässä tapauksessa murto -palkkia pidetään ryhmittelysymbolina eikä divisioonana, joten ylä- ja alaosan toiminnot on ratkaistava:

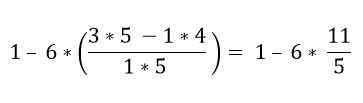
Hierarkkisen järjestyksen mukaan kertolasku on ratkaistava:

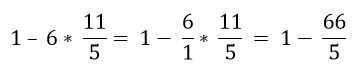
Lopuksi vähennys on ratkaistu: