Mitkä ovat numerot? 8 pääkäyttöä

Se Numerot palvelee Tehtävien äärettömyydelle maailmassa. Useimmissa prosesseissa, esineissä ja paikoissa numerot ovat mukana, vaikka ne eivät aina ilmeisiä. Sen pääkäyttö on, että ne sallivat laskea esineitä.

On vaikeampaa löytää tilanteita, joissa lukuja ei ole mukana. Nämä ovat keskeinen osa monia elämän jokapäiväisiä tilanteita.

Esimerkiksi reitit, jotka tasot määräävät maan koordinaateilla, jotka on muodostettu numeroista; Sama koskee aluksia ja sukellusveneitä, muun muassa.

Numeroiden pääkäyttö

1- Laskeobjektit

Lasten jälkeen numeroiden kanssa opittava ensin on objektien laskeminen, mikä tarjoaa lisätietoja eri tilanteissa.

Esimerkiksi seuraavassa kuvassa on kaksi omenaryhmää.

Molemmat ryhmät sisältävät omenoita. Mutta kun sanotaan, että yhdessä ryhmässä on 3 omenaa ja toisessa ryhmässä on 2 omenaa, eroa ryhmien välillä mainitaan, mikä on omenan määrä kussakin.

Tämä voidaan tehdä kertomalla omenoiden määrän, mikä on mahdollista numeron ansiosta.

2- Operaatiot algebrallinen

Laskennan oppimisen jälkeen lapsille opetettujen lukujen seuraava käyttö liittyy algebrallisiin operaatioihin, kuten summa, vähennys, kertolasku ja jako.

Näitä neljää toimintaa käytetään päivittäin erittäin suurelle määrälle ihmisiä, jotka ovat yksi yleisimmistä lisätäksesi supermarketissa maksettava hinta.

Voi palvella sinua: vaakasuora viiva

3- edustaa rahan arvoa

Ennen rahaa oli, ihmiset tekivät vaihtoa tai vaihtokauppaa heidän kuulumisensa esineiden välillä.

Sitten rahat otettiin käyttöön, mikä helpotti tämän tyyppisiä menettelyjä. Jokaisessa lipussa tai valuutassa ilmestyvä numero edustaa saman arvoa.

Joten tietääksesi kuinka paljon arvoa lipulla on, sinun on vain nähtävä numero, joka sillä on; toisin sanoen sen edustamien rahallisten yksiköiden määrä.

4- Tunnista esineet

Numerot auttavat myös tunnistamaan objekteja. Esimerkiksi seuraavassa kuvassa esitetään kaksi väylää.

Ainoa ero heillä on heidän tunnistuslevy, jolla on numeroita.

Numeroiden ansiosta kunkin bussin omistaja tietää, mikä on sinun. Sama tapahtuu esimerkiksi ihmisten identiteettiasiakirjojen kanssa.

5- binaarinumero

Hyvin yleinen, mutta ei kovin ilmeinen käyttö on binaarilukuja. Binaarinumerot esitetään käyttämällä vain nollia ja joitain.

Esimerkiksi numero 16 binaarilukuina on 10000.

Binaarinumeroita käytetään tietojenkäsittelymaailmassa. Tietokoneiden sisäisesti käsittelevät tiedot edustavat ZERO: ta ja jotkut, koska ne työskentelevät kahdella jännitteellä.

Kun tietokone haluaa lähettää tosiasian, näitä tietoja edustaa binaarikoodi, jossa nolla edustaa jännitetasoa ja yksi edustaa toista jännitetasoa.

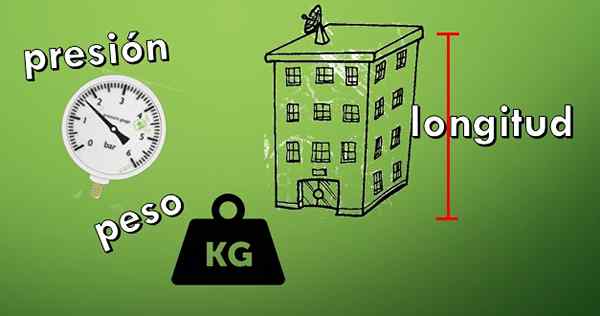
6- Mitta

Objektin pituuden mittaamiseksi lukuja käytetään mittayksikön lisäksi (metrit, mailia).

Voi palvella sinua: Mitkä ovat kolmionumerot? Ominaisuudet ja mielenosoitukset

Sama tapahtuu, kun haluat tietää esineen painon tai ilmanpaine, joka voi tukea polkupyörän kumia.

7- Ne edustavat etäisyyksiä

Numerot ovat ajonneet etäisyydet, joko metriset pituudet tai anglo -saksin järjestelmän mailit. Ja antiikissa jokaisella sivilisaatiolla oli oma tapa laskea etäisyydet, koska se oli enimmäkseen erittäin epätarkkoja ja subjektiivisia.

Itse asiassa on edelleen mahdollista löytää ihmisiä, jotka kysyvät kuinka pitkälle paikka on reagoida "se, mikä vie sikarin", antaen aikayksikön etäisyyden ja ei pituuden esityksenä. 

8- Tilaa kadut

Numerot ovat kansainvälinen tapa löytää jokainen talo, rakennus, paikallinen tai laitos, koska se sijaitsee kadulla ja numerolla. 

Esimerkiksi Espanjassa kadut ovat ikätoverit ja parittomat. Koska ikätoverilla on ikätovereita (2,4,6,8,10 ...) ja toisen jalkakäytävän kanssa samana kadulla, jossa on parittomia lukuja (1,3,5,7,9 ...). Siten Madridin henkilö voi asua Nicasio Gallego -kadulla nro 9.

Viitteet

1. Barker, l. (2011). Matematiikan tasoitetut tekstit: numero ja toiminnot. Opettajan luomat materiaalit.
2. Burton, M., Ranskalainen, c., & Jones, T. (2011). Käytämme numeroita. Vertailuindeksiyhtiö.
3. Doudna, k. (2010). Kukaan ei liimaa, kun käytämme numeroita! Abdo kustantamo.
4. Fernández, J. M. (1996). Kemiallisen sidoslähestymistavan projekti. Palautus.
5. Hernández, J. d -d. (S.F.-A. Matematiikan muistikirja. Kynnys.
6. Lahora, m. C. (1992). Matemaattinen toiminta lasten kanssa 0–6 vuotta. Narcea Editions.
7. Marín, E. (1991). Espanjan kielioppi. Toimitusohjelma.
8. Tocci, r. J -., & Widmer, N. S. (2003). Digitaaliset järjestelmät: Periaatteet ja sovellukset. Pearson -koulutus.

Se voi palvella sinua: 3 neliöjuuri (helppo ratkaisu ja selitys)