Pentadecágono -elementit, luokittelu, ominaisuudet, liikunta

Eräs Pentadecvastakkainen Se on litteä hahmo, joka on rakennettu viidellätoista suoralla segmentillä ja suljellisesti. Tällaisia ​​lukuja kutsutaan monikulmio ja ne on nimetty niiden osapuolten määrän mukaan.

Kolme sivua ja neljästä neljänneksen kolmesta kolmiosta on esimerkkejä hyvin tutuista monikulmioista, mutta monikulmioissa voi olla enemmän puolia.

Kuvio 1.  Säännöllinen viisikulu punaisella kärkipisteellä. Lähde: Wikimedia Commons.

Pentadecágonon peruselementit ovat samat kuin kaikki monikulmiot riippumatta siitä, kuinka. Nämä elementit ovat:

-Puolet, jotka ovat segmenttejä, jotka muodostavat Pentadecágonon yhteensä 15.

-Kärjet, Myös 15, jotka ovat vierekkäisten sivujen päätä.

-Sisäkulmat, Ne, jotka muodostuvat Pentadecágonoon kahden vierekkäisen puolen välillä.

-Ulkokulmat, muodostettu yhden puolen ja yhden peräkkäisen puolen pidentymisen väliin.

-Diagonaalit, Linjasegmentit, jotka liittyvät kahteen ei -adjacent -kärkipisteeseen.

[TOC]

Luokittelu

Pentadecágono voi olla säännöllinen jompikumpi epäsäännöllinen, niiden sivujen koosta ja sen sisäkulmista riippuen. Jos sinulla on kaikki sivut ja yhtäläiset sisäkulmat -Quilátero ja Equiangle - se on säännöllinen, kuten kuvassa 1 esitetään, muuten se on epäsäännöllinen.

Se voidaan myös luokitella kupera jompikumpi kovera. Koveralla Pentagonissa on yksi tai useampi sisäkulma, joka on suurempi kuin 180º, kun taas yhdellä kuperalla on sisäkulmat alle 180º. Tavallinen Pentagon on kupera.

Toiset luokituskriteerit otetaan huomioon, onko sen ei -konseptiota - vai niiden pidennyksiä - leikattuja vai ei. Kun niitä ei leikata, kuten kuvan 1 tapauksessa, sanotaan, että se on yksinkertainen Pentadecágon. Ja jos ne leikataan, se on monimutkainen.

Se voi palvella sinua: analyyttinen geometria

Tavallinen Pentagon

Tavallinen Pentagon, jonka sivuilla ja sisäkulmilla on sama mitta, on suuren symmetrian kuva, koska seuraavat lisäelementit on määritelty aiemmin kuvattuihin:

-Keskusta: Parictices ja sivut Equidista.

-Radio: Etäisyys keskustasta yhteen tavanomaisista viisikulmioista.

-Keskikulma: Se, joka on kärkikortinsa keskellä ja sen sivut kulkevat kahden vierekkäisen kärjen läpi.

-Apoteemi, Se on kohtisuora segmentti, joka liittyy toisen puolen keskustaan ​​kuvan keskustaan.

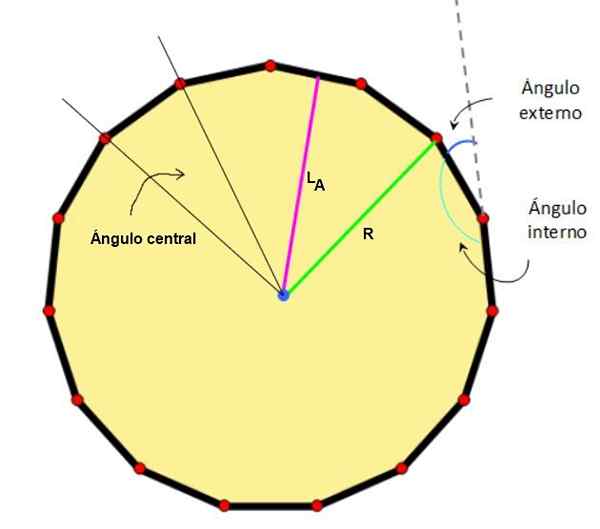Kuva 2. Pentadecágonon keskusta, apoteemi, radio ja merkittävät kulmat Pentadecágono. Lähde: Wikimedia Commons/F. Zapata.

- Tavallisen Pentagonin ominaisuudet

Sisäkulmat

Seuraavaa kaavaa käytetään minkä tahansa tavallisen monikulmion sisäkulmien mittaamiseen I, missä n Se on sivujen lukumäärä:

Tässä kaavassa, mittaan, joka tulee asteina, ilmaista sitä radianeissa, se kerrotaan π/180 -tekijällä. Katsotaanpa, mikä on tavallisen Pentagonin sisäkulmien mitta, korvaamalla n = 15:

I = [(15-2) × 180º]/15 = 156º

Vastaa 13π/15 radiaania. Koska tavallisen Pentagonin sisäkulmat ovat alle 180º, se on kupera monikulmio.

Sisäkulmien summa

Sisäisten kulmien summa on mahdollista laskea seuraavan kaavan avulla:

S = (n-2) x 180º

Kuten aina, n edustaa sivujen lukumäärää. Tämä kaava on voimassa n = 3, 4, 5 .. .

Tekemällä n = 15 saamme:

S = (15 - 2) x 180º = 2340º

Ulkokulmat

Sisäinen kulma ja ulkoinen kulma ovat täydentäviä, toisin sanoen sen summa on 180º, kuten kuvassa 2 todetaan. Siksi Pentadecágonon ulkoinen kulma mittaa:

Voi palvella sinua: Konjugoidut binomial: miten se on ratkaistu, esimerkkejä, harjoituksia

180 º - 156º = 24º.

Kehä ja alue

Ympäristö on monikulmion muodon mitta ja lisää helposti kaikki puolet. Joo -lla Se on sivun pituus, se riittää moninkertaistumaan n, Sivujen lukumäärä.

Tavalliselle Pentagonille A: lle kehä P on:

P = 15a

Jos se on epäsäännöllinen luku, jossa sivujen mitta eroaa, kehä lisää kaikkien sivujen pituuden.

Alueen osalta voimme laskea sen monin tavoin. Esimerkiksi meillä on kaava, jonka avulla voit hankkia sen tietäen sen sivujen pituuden:

Suorittaessaan ilmoitettuja toimintoja se pysyy suunnilleen:

A = 17 6426⋅A²

On toinen vaihtoehto, jota voidaan soveltaa tavallisiin monikulmioihin. Kyse on niiden jakamisesta pohjakolmioihin, jotka ovat yhtä suuret kuin monikulmio. Kolmion korkeus on apoteemin l pituus_-Lla, yllä määritelty.

Mainitun kolmion pinta -ala on laskettu hyvin tunnetulla kaavalla: pohja x korkeus /2. Tällä tavoin yksittäinen kolmioalue on:

Alue = a. Lens_-Lla /2

Jotta monikulmion kokonaispinta -ala on, se riittää moninkertaistumaan sivujen n lukumäärällä, mikä tässä tapauksessa on 15:

A = 15⋅ a⋅ l_-Lla /2

Ja koska kuvan kehä on P = 15⋅A, niin:

A = p⋅ l_-Lla /2

Diagonaalit

Diagonaalit ovat segmenttejä, jotka yhdistävät kaksi ei -peräkkäistä kärkipistettä, kuten edellä todettiin. Tietää kuinka monta diagonaalista tavallinen monikulmio on n Sivut, mukaan lukien Pentadecágono, on seuraava kaava:

Missä d on diagonaalien lukumäärä.

Nyt korvaamme n = 15, jotta saadaan kokonais diagonaalit:

Voi palvella sinua: säännölliset monikulmiot: ominaisuudet, elementit, kulmat, esimerkit

D = [15 × (15-3)]/2 = 90 diagonaalia.

Rakentaminen sääntöllä ja kompassilla

Pentadecágono on rakennettu sääntöllä ja kompassilla kehästä alkaen. 360º on jaettava 15 yhtä suureen osaan 24º: ta. Ensin animaatiossa ilmoitetut apurakenteet suoritetaan 60º kulman saamiseksi, joka on jaettu vuorotellen 36º: een ja 24º.

Kuva 3. Rakentaminen säännöllisen pentagonin sääntöllä ja kompassilla. Lähde: Wikimedia Commons.

Liikuntaa

Jos säde ympyrään R -ympyrään R -ympyrään on 12,56 cm, jos Pentadecágonon kehä. Laskea:

a) radio.

b) Alueesi.

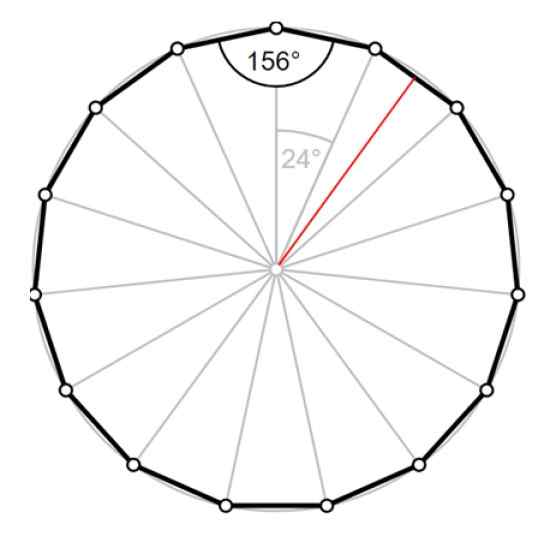Kuva 4. Pentadecágono: Keskuskulma, sisäinen kulma ja punainen apoteema. Lähde: Wikimedia Commons/F. Zapata.

Liittää jhk

Kehä on p = 15⋅a = 12.Siksi 56 cm, puoli Pentadecágono on 0.8373 cm. Radio Voimme laskea sen kuvan 4 yhden kolmion avulla.

Apoteemi l_-Lla vastaa punaisella piirrettyjen kolmion korkeutta, joka jakaa 24º kulman kahteen 12º kulmaan.

On olemassa kaksi oikeaa kolmiota, joiden sisäinen kulma on 12º, ja mihin tahansa niistä voimme levittää trigonometriaa hypotenuksen löytämiseksi, mikä on säteen pituus R.

Tällä tavalla:

SEN 12º = (A /2) /R

R = (A /2) /Sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Ratkaisu b

Voimme laskea Pentadecágonon alueen kaavalla:

A = p⋅ l_-Lla /2

Tiedämme jo kehän p = 12.56 cm, ja apoteemin pituus lasketaan tangentin tai 12º kosinin avulla:

Cos 12º = l_-Lla / R

Lens_-Lla = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Korvaus:

A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm²

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Opi matematiikkaa. Geometriset luvut. Toipunut: Rodrigoanchorena.Wixsite.com.
3. Sangaku -matematiikka. Monikulmion ja sen luokituksen elementit. Toipunut: Sangakoo.com.
4. Wikipedia. Pentadecágono. Palautettu: on.Wikipedia.org.
5. Wolfram Math World. Pentadekagoni. Toipunut: MathWorld.Susi.com.