Y = 3Sen (4x) toimintojakso

Hän Y = 3Sen (4x) toimintojakso Se on 2π/4 = π/2. Tämän lausunnon syyn ymmärtämiseksi selkeästi funktion ajanjakson määritelmä ja sen (x) -funktion ajanjakso on tiedettävä; Hieman funktiokaavio on myös hyödyllinen.

Trigonometriset toiminnot, kuten sinus ja kosini (Sen (x) ja cos (x)), ovat erittäin hyödyllisiä sekä matematiikassa että tekniikassa.

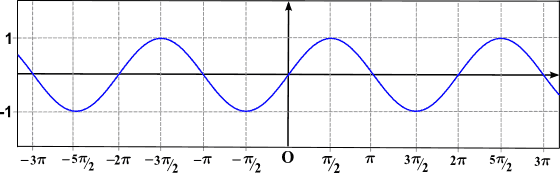
Sanajaksossa mainitaan tapahtuman toisto, joten funktio on määräajoin yhtä suuri kuin sanominen "sen kuvaaja on käyrän kappaleen toisto". Kuten edellisessä kuvassa voidaan nähdä, sen (x) -toiminto on jaksollinen.

Säännölliset toiminnot

Funktion f (x) sanotaan olevan jaksollinen, jos on olemassa todellinen arvo p ≠ 0 siten, että f (x+p) = f (x) kaikille x: lle funktion alueella. Tässä tapauksessa funktion ajanjakso on P.

Sitä kutsutaan yleensä funktion ajanjaksoksi alhaisimmalla positiivisella reaaliluvulla P, joka täyttää määritelmän.

Kuten edellisessä kaaviossa voidaan nähdä, sen (x) -funktio on jaksollinen ja sen ajanjakso on 2π (kosinifunktio on myös jaksollinen, jakso on yhtä suuri kuin 2π).

Funktion kuvaajan muutokset

Olkoon f (x) funktio, jonka kaavio tunnetaan ja olla positiivinen vakio. Mitä tapahtuu f (x) -kaaviolle, jos kerrotaan f (x) c: llä? Toisin sanoen, kuinka kaavio on c*f (x) ja f (cx)?

C*f -kuvaaja (x)

Kertoamalla funktio ulkoisesti positiivisella vakiolla F (x) -kaavio muuttuu lähtöarvoihin; Eli muutos on pystysuoraan ja kaksi tapausta voidaan ottaa:

- Jos c> 1, niin kaavio kärsii pystysuorasta venytyksestä C -tekijän kanssa.

- Kyllä 0

F Grafi (CX)

Kun funktion argumentti kerrotaan vakiona, f (x) -kaavio kärsii tuloarvoissa; Eli muutos on vaakasuorassa ja kuten ennenkin, kaksi tapausta voidaan ottaa:

- Jos c> 1, niin kaavio kärsii vaakasuorasta puristuksesta kertoimella 1/c.

- Kyllä 0

Y = 3Sen (4x) toimintojakso

On huomattava, että funktiossa f (x) = 3se (4x) on kaksi vakiota, jotka muuttavat sinusfunktion kuvaajaa: yksi moninkertaistaa ulkoinen ja toinen sisäisellä tavalla.

Kolme, joka on sinifunktion ulkopuolella, on laajentaa funktio pystysuoraan kertoimella 3. Tämä tarkoittaa, että 3Sen-funktiokaavio (x) on arvojen välillä -3 ja 3.

Sinisfunktion sisällä oleva.

Toisaalta funktion ajanjakso mitataan vaakasuoraan. Koska sen (x) -funktion ajanjakso on 2π, kun tarkastellaan syntiä (4x), ajan koko muuttuu.

Tietää, mikä on Y = 3Sen (4x) -jakso, vain kerrotaan sen (x) -funktion ajanjakso 1/4 (pakkauskerroin).

Toisin sanoen funktion ajanjakso y = 3Sen (4x) on 2π/4 = π/2, kuten viimeisessä grafiikassa voidaan nähdä.