Paino (fyysinen) laskelma, yksiköt, esimerkit, harjoitukset

Hän paino Se on voima, jolla maa houkuttelee esineitä sen pintaan. Joka kerta, kun esine pudotetaan, tämä on menossa maahan, se ei pysty kiipeämään omia keinojaan eikä se ole asentamaton puolivälissä, mikä johtuu siitä, että maa houkuttelee sitä.

Kaikki esineet houkuttelevat aina toisiaan, jopa pieniä, vain että sen voiman suuruus, jolla he tekevät, on verrannollinen massaan. Tämä tarkoittaa, että pienillä massalla olevilla esineillä on vähän voimaa muihin nähden, mutta taivaalliset kappaleet, kuten maa, kykenevät käyttämään erittäin suurta voimaa.

Maa pitää kuu kiertävän sen ympärillä tämän vetovoiman voiman ansiosta, jota kutsutaan Painovoima Kun kyse on esineistä, jotka ovat kaukana maan pinnasta, ja paino Kun esineet ovat lähellä.

Tämä seuraa, että painovoima ei vaadi, että esineet ovat välttämättä kosketuksissa toisiinsa toimimaan: siksi sanotaan, että se on etäisyysvoima toimintavoima.

Esineillä on edelleen paino.

Suuri englantilainen tiedemies Isaac Newton antoi ensimmäisenä selityksen tästä aiheesta yleismaailmallisen gravitaatiolain kautta, joka kantaa hänen nimensä ja joka on siitä lähtien ymmärtänyt, kuinka esineet ovat vuorovaikutuksessa Massan kanssa massalla. Tämä on erittäin tärkeää, koska jokaisella planeetan kohteilla on paino.

[TOC]

Painoyksiköt

Kansainvälinen yksikköjärjestelmä, jos paino on paino Newton, nimetty Isaac Newtonin kunniaksi. Tämä on yksikkö kaikenlaisten voimien mittaamiseksi.

Newton, lyhennetty N, määritellään tarvittavaksi voimana 1 kg: n massasobjektille 1m/s kiihtyvyyden hankkimiseksi². Newtonin lisäksi on olemassa muita yleisen käytön voiman yksiköitä, esimerkiksi seuraavat:

Kilogrammi

Hän kilogrammi o Kilopondio, lyhennetty KG-F tai KP, vaikka yleisesti kutsutaan kg ilman enempää. Sijainti on välttämätöntä määrittää, koska kuten todettiin, gravitaatiokenttä kokee vaihtelut korkeudella ja leveysasteella.

Kun joku sanoo, että painaa 45 kg, todellisuudessa se tarkoittaa, että heidän paino on 45 kg-F, koska kilogrammi on massalle varattu yksikkö.

Voi palvella sinua: Avoin piiri

KG-F: n ja N: n välinen vastaavuus on: 1kg-F = 9.8 n

Punta-voima

Se Vaaka-Fuerza, Lyhennettyä LB-F on myös KG-F: n analoginen voimayksikkö, koska se on voima, jota maa käyttää 1 naulaa massaa. Ja kuten KG-F: n kohdalla, arvoilla ei ole mitään ongelmaa, kun olet maan päällä, ts.

Vastaavuus LB-F: ssä ja N: ssä on: 1 lb-f ≡ 4.44822 n.

Painonlaskenta ja kaava

Kohteen paino on verrannollinen sen massaan. Suurempi massa, suurempi paino.

Kaava painon p (tai myös w, kuten joskus tarkoittaa "Paino" Englanniksi) se on hyvin yksinkertainen:

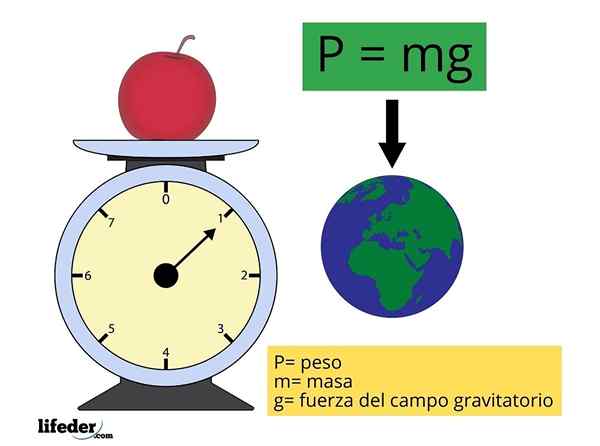
P = mg

Missä m edustaa esineen massaa ja g Se on painovoiman kiihtyvyyden suuruus (gravitaatiokentän voimakkuus tai vakavuus), suunnilleen vakio ja jonka arvoa otetaan 9.81 m/s² Yleisimpiä laskelmia.

Paino on vektori ja vektorin ja sen suuruuden erottamiseksi lihavoitu kirjaimia käytetään. Tällä tavalla, kun puhut p: stä, ymmärretään, että se on numeerinen arvo ja kun se on kirjoitettu P Viittaus vektoriin:

P = m ∙g

Se g Rohkeilla sanoituksilla se on maan gravitaatiokenttä, toisin sanoen sen ympäröivän tilan vaikutuksen, riippumatta siitä, onko se toinen ruumis, joka havaitsee sen. Jokaisella massalla olevalla esineellä on oma painovoimakenttä, olipa se pieni tai suuri.

Maan gravitaatiokentän voimakkuus g Se ei ole täysin vakio. Sillä on pieniä variaatioita, jotka syntyvät pääasiassa siksi, että maa ei ole täydellinen pallo ja myös paikallisille korkeuksille ja tiheyseroille. Mutta useimmissa sovelluksissa, arvo 9.81 m/s² Se toimii erittäin hyvin.

Muilla taivaankappaleilla on oma ominainen gravitaatiokenttä, joten painovoiman kiihtyvyys eroaa planeetan tai satelliitin mukaan. Samalla esineellä olisi erilainen paino kussakin, joten paino ei ole asioiden tyypillinen ominaisuus, vaan yleensä aihe.

Paino vektorina

Paino on vektori, ja siksi sillä on suuruus, suunta ja merkitys. Maapallon pinnan läheisyydessä paino on pystysuora vektori ja suunta on aina alhaalla.

Yleensä pystysuuntainen osoite nimitetään akseliksi ja jompikumpi z -z, Ja merkitys on määritetty merkki + tai merkki - sen erottamiseksi suunnasta ylöspäin. Valinta riippuu alkuperän sijainnista. Alemmassa kuvassa alkuperä valittiin siinä vaiheessa, josta Apple putoaa:

Voi palvella sinua: Ihanteellinen kaasu: malli, käyttäytyminen, esimerkit Paino on vektori, joka on suunnattu pystysuoraan. Lähde: f. Zapata.

Yksikkövektori J -, Suuruusluokan vektoria käytetään yhtä. Tämän vektorin suhteen paino on kirjoitettu näin:

P = mg ( - J --A

Missä negatiivinen merkki osoitetaan suuntaan.

Erot painon, massan ja tilavuuden välillä

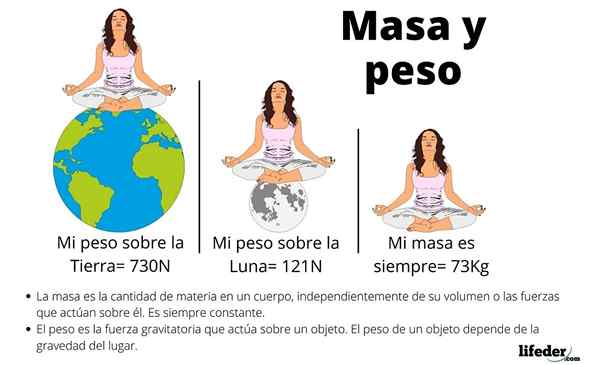
Usein nämä kolme käsitettä ovat hämmentyneitä, mutta tarkistamalla painon ominaisuuksia on helppo erottaa se massasta ja tilavuudesta.

Aluksi paino riippuu esineen paikan painovoimakentästä. Esimerkiksi maapallolla ja kuussa samalla asialla on erilainen paino, vaikka sen muodostavien atomien määrä on vakio.

Massa on skalaarinen suuruus, joka liittyy esineen muodostavien atomien määrään ja todistetaan vastustuskyvyn kanssa, joka esineen on muutettava liikettä, ominaisuus nimeltään inertia.

Sen puolestaan ​​tila on objektin miehittämä tilan mitta, toinen skalaarinen määrä. Kaksi yhtä suurta tilavuutta olevaa esinettä eivät paina samaa, esimerkiksi rautakuutio painaa paljon enemmän kuin toinen samojen mittojen polystyreeni.

Yhteenvetona:

• Massa liittyy kehon aineen määrään.
• Paino on maa, jonka maa on käyttänyt kyseiseen massaan, verrannollinen siihen.
• Tilavuus on aterian käyttämä tila.

On huomattava, että skalaarisia määriä, massalla tai tilavuudella ei ole suuntaa tai merkitystä, vaan vain numeerinen arvo ja riittävä yksikkö. Toisaalta paino, vektori, on aina ilmaistava oikein osoittamalla suuruus, yhtenäisyys, suunta ja merkitys, kuten edellisessä osassa.

Esimerkkejä painosta

Kaikilla maan esineillä on paino, voit jopa "punnita" esineitä, jotka eivät ole maan päällä, kuten muita planeettoja tai aurinkoa, vaikka epäsuorilla keinoilla se on tietysti.

Koska painoalue on erittäin suuri, käytetään tieteellistä merkintää (10: n voimissa) ilmaistakseen joitain, jotka ovat erittäin suuria tai erittäin pieniä:

-Aurinko: 1 989 × 10³⁰ KG-F

-Jupiter: 1 898 × ​​10²⁷ KG-F

-Hyttyset: 2.0 × 10^-5 N

-Vauvat: 34.3 n

-Lapsi: 353 n

-Aikuinen henkilö: 65 kg-F

-Aikuinen norsu: 5.5 × 10³ KG-F

-Sininen valas: 1.0 × 10⁶ N

Liikuntaa

Taikina -laatikko 20 kg lepää pöydällä.

a) Löydä laatikon paino ja taulukon normaali voima.

Voi palvella sinua: lineaarisen vauhdin säilyttäminen: periaate, esimerkit, harjoitukset.

b) Toinen 10 kg: n laatikko on asetettu ensimmäiseen. Löydä normaali, jonka taulukko harjoittaa 20 kg: n laatikossa ja normaalilla tavalla, jota se käyttää pienimmässä laatikossa.

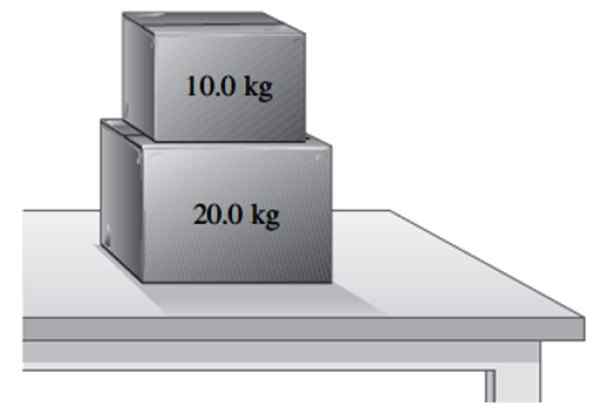Kaksi laatikkoa lepäävät pöydällä. Lähde: f. Zapata.

Liittää jhk

On kätevää tehdä ilmainen runkokaavio laatikossa, joka koostuu siihen, että piirtävät siihen vaikuttavat voimat.

Tässä tilanteessa päällä on edelleen pienin laatikko, joten voimia on vain kaksi: ensimmäinen on paino P joka vedetään pystysuoraan, kuten edellisissä osissa on osoitettu ja sitten on normaali N, joka on kohtisuora voima, jota taulukko käyttää ja estää laatikon putoamisen.

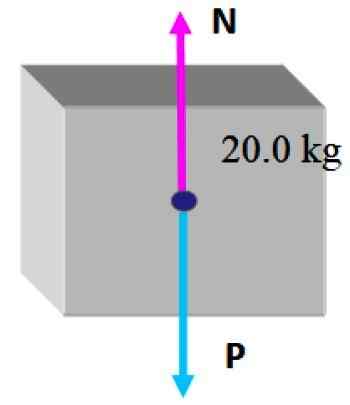
Koska laatikko on staattisessa tasapainossa näissä olosuhteissa, on kohtuullista päätellä, että normaalin suuruus on sama kuin painon, jotta se voi kompensoida, siksi:

N = mg = 20.0 kg x 9.8 m/s² = 196 n; Pystysuoraan suuntautuva.

Paino on puolestaan ​​P = 196 n ohjattu pystysuoraan alaspäin.

Ratkaisu b

Nyt molemmista esineistä tehdään uusia ilmaisia ​​kehon kaavioita. Sillä iso laatikko muuttuu hiukan, koska pieni laatikko käyttää sitä voimaa.

Voimat ovat seuraavat: N ja P Ne ovat vastaavasti normaalit, jotka taulukon harjoitukset ja 20 -laatikon paino.0 kg, se ei muuttunut. Ja pieni pienen laatikon aiheuttama joukko on N₁, normaali, joka johtuu kosketuksesta ison laatikon yläpinnan kanssa.

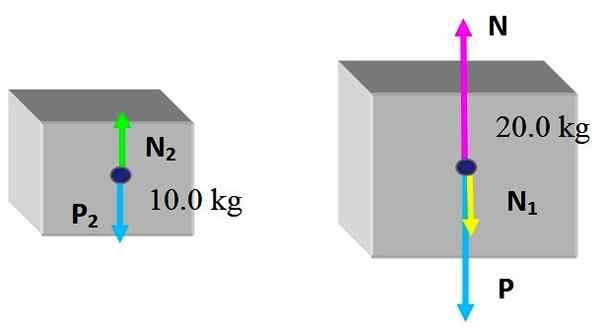
Pienen laatikon suhteen se vastaanottaa normaalin N₂, Ison laatikon yläpinta ja tietysti sen paino P₂. Koska laatikot ovat staattista saldoa:

N₂ - P₂ = 0

N - n₁ - P = 0

Ensimmäisestä yhtälöstä sinun täytyy₂ = P₂ = 10 kg x 9.8 m/s² = 98 n. Toiminta- ja reaktiolain mukaan pienen laatikon vastaanottaman voiman suuruus on sama, jota se käyttää suureen laatikkoon, sitten:

N₂ = N₁ = 98 n

Toisesta yhtälöstä normaali n, jonka taulukko harjoittaa isoa laatikkoa, puhdistetaan, mikä puolestaan ​​on pieni laatikko päällä:

N = n₁ + P = 98 n + 196 n = 294 n

Viitteet

1. Figueroa, D. 2005. Sarja: Tieteen ja tekniikan fysiikka. Nide 2. Dynaaminen. Toimittanut Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysiikka. Toinen. Ed. McGraw Hill.
3. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
5. Serway, R., Jewett, J. 2008. Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
6. Thomas Griffith, W. 2007. Käsitteellinen fysiikka. MC Graw Hill.